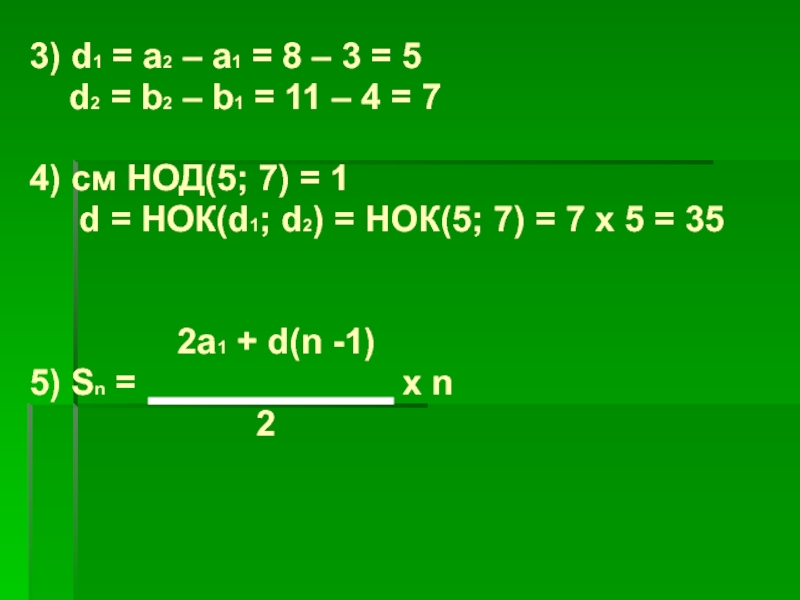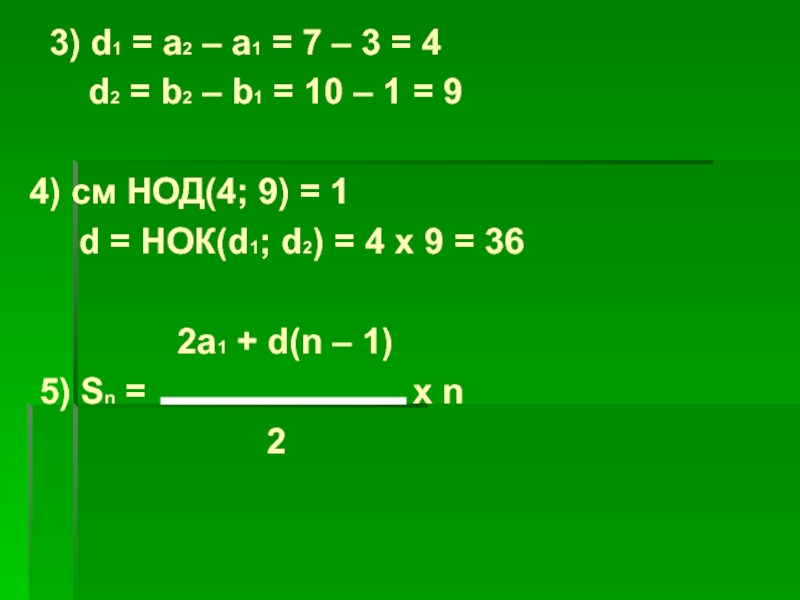Слайд 1МАОУ «СОШ № 1» с углублённым изучением отдельных предметов имени
И. А. Куратова г.Сыктывкара.
Исполнитель: Лукина Серафима
Руководитель: Карпова Людмила Александровна
2011 год.
Одно
из свойств
арифметических прогрессий.
Слайд 2Эпиграф
Через математические знания, полученные в школе, лежит широкая дорога к
огромным, почти необозримым областям труда и открытий.
Маркушевич А. И.
Слайд 3
Доказать одно из свойств арифметических прогрессий и воспользоваться им на
практике.
Цель исследовательской
работы:
Слайд 4Арифметическая прогрессия - это последовательность, каждый член которой, начиная со
второго, равен предыдущему, сложенному с одним и тем же числом.
аn = a1 + d(n – 1)
d = an + 1 – аn
а1 + аn
Sn = x n
2
2а1 + d(n – 1)
Sn = x n
2
Слайд 5
7.32.
1) Найдите сумму первых 20 совпадающих членов двух арифметических
прогрессий:
3, 8, 13, … и 4, 11, 18,
… .
2)Найдите сумму первых 10 совпадающих членов двух арифметических прогрессий:
3, 7, 11, … и 1, 10, 19, … .
Слайд 6Первый совпадающий член двух данных прогрессий можно найти, непосредственно выписав
несколько последовательных членов каждой из них.
d = НОК(d1;
d2)
d1 – разность первой прогрессии
d2 – разность второй прогрессии
« Действительно ли это так и можно ли это доказать?»
Слайд 71) НОК(Наименьшим общим кратным) натуральных чисел а и b называют
наименьшее натуральное число, которое кратно и а, и b.
Пример: НОК(6; 8) = 24
2)Если НОД(а; b) = 1, т. е. числа а и b взаимно простые, то НОК(а; b) = a x b
Пример: а = 3; b = 4
НОД(3; 4) = 1
НОК(3; 4) = 3 x 4 = 12
Слайд 8
Если а : b и а : c
a : b x c
НОК(Ra; Rb)
= RНОК(а; b), где
НОД(а; b) = 1
Слайд 9Дано: (аn) и (bn) – арифметические прогрессии, соответственно с разностями
d1 и d2, НОД(d1;d2) = 1;
(сn) содержит совпадающие члены
данных последовательностей, d – разность прогрессии
Доказать: d = НОК(d1; d2) = d1 x d2
Доказательство:
1) см (сn) и (аn)
с1 = аR = а1 + d1(R – 1)
c2 = al = a1 + d1(l – 1)
Слайд 10См d = c2 – c1 = al – aR
= a1 – a1 + d1(l – R) =
=
d1(l – R) d : d1
2)см (сn) и (bn)
с1 = bm = b1 + d2(m – 1)
c2 = bp = b1 + d2(p – 1)
см d = c2 – c1 = d2(m – p) d : d2
Вывод:
1)d : d1
d : d1 x d2 d = НОК(d1; d2)
d : d2 НОД(d1;d2) = 1
Слайд 11См примеры:
1) 12 : 4
12 =
НОК(4; 3);см НОД(4;3) = 1
12 : 3
Получено 12 = НОК(4; 3) = 4 x 3
2) см 24 : 6
24 = НОК(6; 8); см НОД(6; 8)=1
24 : 8
24 = НОК(6;8) = 6 x 8
Значит: если НОД(d1; d2) = 1,
то d = НОК(d1;d2) = d1 x d2
Слайд 12Примечание:
Свойство НОК:
Если а и b – не взаимно
простые числа,
НОК(Ra; Rb) = RНОК(а; b),
НОД(а; b) = 1
См пример:
НОК(6;8)
= НОК(2 x 3; 2 x 4) = 2НОК(3; 4) =
= 2 x 12 = 24
Слайд 137.32.
1)Найдите сумму первых 20 совпадающих членов двух арифметических прогрессий:
3, 8, 13, …
4, 11, 18, … .
Решение:
1) S20 - ?
2) (аn): 3, 8, 13, 18, …
(bn): 4, 11, 18, …
(сn): 18, …
Слайд 14
3) d1 = a2 – a1 = 8 –
3 = 5
d2 = b2 – b1 =
11 – 4 = 7
4) см НОД(5; 7) = 1
d = НОК(d1; d2) = НОК(5; 7) = 7 x 5 = 35
2a1 + d(n -1)
5) Sn = x n
2
35(20 – 1)
S20 =
x 20 =
2
36 + 35 x 19 701
= x 20 = x 20 = 7010
2 2
Ответ: S20 = 7010
Слайд 16 2) Найдите сумму первых 10 совпадающих членов двух
арифметических прогрессий:
3, 7, 11, … и
1, 10, 19, …
Решение:
1) S10 - ?
2) (an): 3, 7, 11, 15, 19, …
(bn): 1, 10, 19, …
(сn): 19, …
Слайд 17 3) d1 = a2 – a1 = 7 –
3 = 4
d2 = b2 – b1
= 10 – 1 = 9
4) см НОД(4; 9) = 1
d = НОК(d1; d2) = 4 x 9 = 36
2a1 + d(n – 1)
5) Sn = x n
2
– 1)
S10 =
x 10 =
2
38 + 36 x 9 362
= x 10 = x 10 = 1810
2 2
Ответ: S10 = 1810
Слайд 1912.98.
В арифметической прогрессии 3; 6; 9; … содержится
463 члена, в арифметической прогрессии 2; 6; 10; … содержится
351 член. Сколько одинаковых членов содержится в этих прогрессиях.
Решение:
1) n - ?
(аn): 3, 6, 9, … (463 члена)
(bn): 2, 6, 10, … (351 член)
(сn): 6, …
Слайд 20
2) d1 = a2 – a1 = 6
– 3 = 3
d2 = b2 –
b1 = 6 – 2 = 4
3) cм НОД(3; 4) = 1
d = НОК(d1; d2) = НОК(3; 4) = 3 x 4 = 12
4) cм аn = а1 + d(n – 1)
а463 = 3 + 3(463 – 1) = 1389
b351 = 2 + 4(351 – 1) = 1402
Слайд 21 5) сn = c1 + d(n – 1); n
- ?
6 + 12(n – 1)
1389
6 + 12(n – 1) 1402
6 + 12n – 12 1389
6 + 12n – 12 1402
12n 1395
12n 1408
n 116, 25
n 117, 33
n = 116
Ответ: 116 одинаковых членов содержится в этих прогрессиях.
Слайд 22В заключении строки из романа А. С. Пушкина «Евгений Онегин»,
сказанные о его герое: «…Не мог он ямба от хорея,
как мы не бились, отличить».Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.
Слайд 23Ямб – стихотворный размер с ударениями на чётных слогах стиха
(н: Мой дядя самых честных правил), т. е. ударными являются
второй, четвёртый, шестой, восьмой и т. д. слоги. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2, 4, 6, 8… .
Слайд 24 Хорей – стихотворный размер с ударением
на нечётных слогах (н: Буря мглою небо кроет). Номера ударных
слогов также образуют арифметическую прогрессию, но её первый член равен единице, а разность по-прежнему равна двум: 1; 3; 5; 7, … .
Слайд 25Практическая значимость
1)Моя работа может использоваться на уроках алгебры при изучении
темы «Арифметические прогрессии».
2)Данное исследование поможет учащимся при написании
ГИА и ЕГЭ.
Слайд 26Сборник заданий для подготовки к ГИА в 9 классе;
Сборник задач по алгебре(8-9 класс) М.Л. Галицкого, А. М. Гольдмана,
Л. И. Звавича;
Учебник для 9 класса с углублённым изучением математики Ю. Н. Макарычева, Н. Г. Миндюка, К. И. Нешкова;
Пособие для учителя «Делимость целых чисел» В. Д. Яковлева;
Учебное пособие для учащихся школ и классов с углублённым изучением математики(для 9 класса) под редакцией Н. Я. Виленкина.
Источники: