Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку по теме "Решение линейных неравенств с одной переменной"
Содержание
- 1. Презентация к уроку по теме "Решение линейных неравенств с одной переменной"
- 2. Решение неравенств с одной переменной«Знания, которые не пополняются ежедневно, убывают с каждым днём»Французская пословица
- 3. АрхимедПонятиями неравенства пользовались уже древние греки. Архимед
- 4. Понятия «больше» и «меньше» наряду с понятием
- 5. Эпоха ЕвклидаВо времена ПтолемеяII в Александрии был
- 6. Современные знаки неравенств появились лишь в XVll
- 7. «Считай несчастным тот день или тот час,
- 8. Невозможно изучить новое без повторения уже изученного.I, Устная работа.-Закончите предложение, чтобы получилось верное утверждение:
- 9. Определение Запись вида a > b (a
- 10. Свойства равносильности неравенствЛюбой член неравенства можно переносить
- 11. Алгоритм решения неравенств первой степени с
- 12. Устная работа 1) Перед вами неравенства, их
- 13. Устная работа2) Какие из указанных чисел 2;
- 14. Закрепление изученного материалаРабота в парах (тест )1.
- 15. Химический опыт Перед вами эталонная шкала для
- 16. «Скажи мне , и я забудуПокажи мне,-
- 17. Поисковая работа Решить неравенство:1-я группа : 1)
- 18. 1) х - 0,25(х + 4)
- 19. Слайд 19
- 20. Готовимся к ОГЭ «Применение неравенств» и
- 21. 2. Между какими двумя
- 22. 3. Сколько целых чисел удовлетворяет неравенству -23,1≤ a ≤ 231,1?
- 23. Готовимся к ОГЭ1) Задача. В типографию поступил
- 24. Домашнее задание: учебник: №855 (в, г), №847
- 25. Кто круга от квадрата не может отличить,Тому
- 26. Реши задачиI. Найдите наибольшее целое число,
- 27. Решение задачи I.I. Найдите наибольшее
- 28. Решение задачи II. 0,2(2х+2) - 0,5(х-1)
- 29. Решение задачи III.
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Решение неравенств
с одной переменной
Презентацию подготовила
учитель математики
МБОУ «Фокинская средняя
общеобразовательная
школа №3»
Слайд 2Решение неравенств
с одной переменной
«Знания, которые не пополняются ежедневно, убывают
с каждым днём»
Французская пословица
Слайд 3Архимед
Понятиями неравенства пользовались уже древние греки.
Архимед (lll в. до
н. э.), занимаясь вычислением длины окружности, установил, что «периметр всякого
круга равен утроенному диаметру с избытком, который, меньше седьмой части диаметра, но больше десяти семьдесят первых». Иначе говоря, Архимед указал границы числаСлайд 4Понятия «больше» и «меньше» наряду с понятием равенства возникли в
связи со счетом предметов и необходимостью сравнивать различные величины.
Большинство из нас привычно пользуются математическими символами, не задумываясь, кто же именно и когда их придумал. Так, привычные нам знаки сложения и вычитания появились в конце XV в. благодаря знаменитому учёному Я. Видману. А знак равенства ввёл англичанин
Р. Рекорд в 1557г.
Слайд 5Эпоха Евклида
Во времена ПтолемеяII в Александрии был создан очаг муз,
вроде наших университетов и академий. Он имел выдающуюся библиотеку и
первую государственную коллекцию греческих рукописей. Ещё при правлении ПтолемеяI в Александрии начинает свою деятельность Евклид, написавший его основные сочинения “Элементы” и “Начала”.Слайд 6Современные знаки неравенств появились лишь в XVll – XVlll вв.
Знаки < и > ввел английский математик Томас Гарриот (1560
-1621). Знаки ≤ и ≥ французский математик П. Буге (1698 -1758).Отдельные свойства систем линейных неравенств рассматривались еще в первой половине IX века в связи с некоторыми задачами аналитической механики.
Систематическое же изучение систем линейных неравенств началось в самом конце IX века, однако о теории линейных неравенств стало возможным говорить лишь в конце двадцатых годов xx века, когда уже накопилось достаточное количество связанных с ними результатов.
Слайд 7
«Считай несчастным тот день или тот час,
в который ты
не усвоил ничего и
ничего не прибавил к своему образованию»
(Я.А. Каменский – чешский
педагог - гуманист, писатель)
Существуют три главных правила хорошей учебы:
Учить теорию.
Решать задачи самостоятельно.
Исправлять ошибки.
Слайд 8Невозможно изучить новое без повторения уже изученного.
I, Устная работа.
-Закончите предложение,
чтобы получилось верное утверждение:
Слайд 9Определение
Запись вида a > b (a ≥ b) или
a < b
(a ≤ b ) называется неравенством.
Неравенства вида a
≥ b, a ≤ b называются ……нестрогими
Неравенства вида a < b, a > b называются ……
строгими
Слайд 10Свойства равносильности неравенств
Любой член неравенства можно переносить из одной части
неравенства в другую, изменив его знак на противоположный, при этом
знак неравенства не меняется.Обе части неравенства можно умножить или разделить на одно и тоже положительное число, при этом знак неравенства не изменится. Если a > b, c > 0, то ac > bc.
Если это число отрицательное, то знак неравенства изменится на противоположное.
Слайд 11Алгоритм решения неравенств
первой степени с одной переменной
Раскрыть скобки и
привести подобные слагаемые.
Сгруппировать слагаемые с переменной в левой части неравенства,
а без переменной – в правой части, при переносе меняя знаки.Привести подобные слагаемые.
Разделить обе части неравенства на коэффициент при переменной, если он не равен нулю.
Изобразить множество решений неравенства на координатной прямой.
Записать ответ в виде числового промежутка.
Слайд 12Устная работа
1) Перед вами неравенства, их геометрические интерпретации и
записи соответствующих числовых промежутков, но всё перепутано. Необходимо восстановить истинную
картину.Неравенство Решение Графическая иллюстрация
1. X<5 1. [5;+∞) 1.
2. x≥5 2. (5; +∞) 2.
3. 5
4. 5≥x 4. (-∞;5) 4.
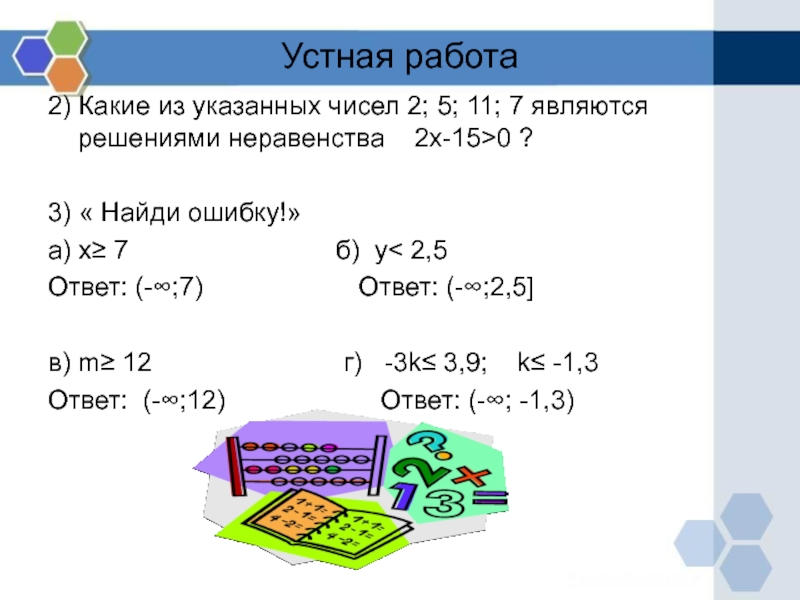
Слайд 13Устная работа
2) Какие из указанных чисел 2; 5; 11; 7
являются решениями неравенства 2х-15>0 ?
3) « Найди ошибку!»
а) х≥
7 б) у< 2,5Ответ: (-∞;7) Ответ: (-∞;2,5]
в) m≥ 12 г) -3k≤ 3,9; k≤ -1,3
Ответ: (-∞;12) Ответ: (-∞; -1,3)
Слайд 14Закрепление изученного материала
Работа в парах (тест )
1. Является ли число
-5 решением неравенства 2х≥10 ?
2. Является ли
число 6 решением неравенства 2х≥10 ? 3. Является ли неравенство 2х+8≥3 строгим?
4. Соответствует ли неравенство -1≤х≤5 промежутку( -2;5)?
5. Соответствует ли промежуток (5; 0) неравенству Х≤5 ?
6. Число 8 является наименьшим целым числом неравенства Х≥8 ?
Слайд 15Химический опыт
Перед вами эталонная шкала для водородного показателя pH,
в пределах от 0 до 12.
Если показатель 0
≤ pH < 7, то среда кислая;если показатель pH = 7, то среда нейтральная;
если показатель 7< pH ≤ 12, то среда щелочная
Слайд 16
«Скажи мне , и я забуду
Покажи мне,- и я смогу
запомнить.
Позволь мне сделать это самому,
И это станет моим навсегда».
Древняя
мудрость.Слайд 17Поисковая работа
Решить неравенство:
1-я группа : 1) х
- 0,25(х + 4) + 0,5(3х - 1) > 3;
2-я группа : 2) х² + х < х(х - 5) + 2.
Слайд 18
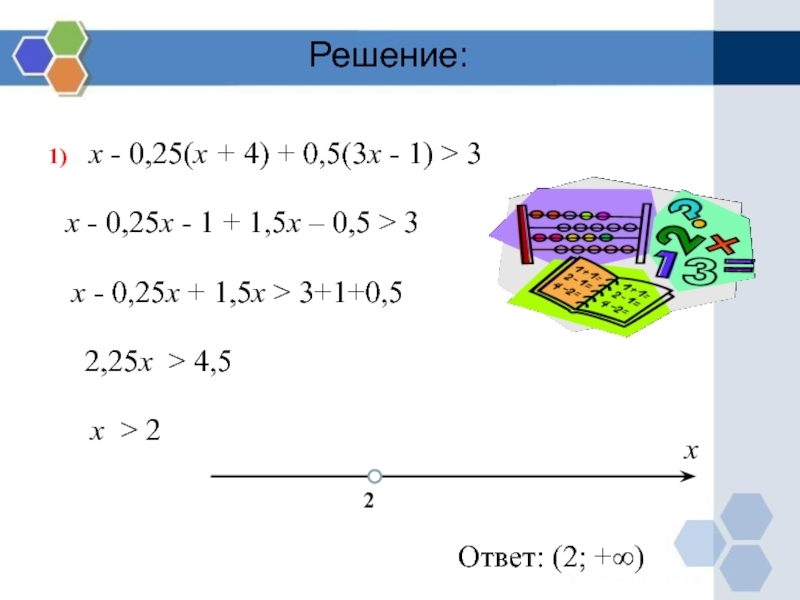
1) х - 0,25(х + 4) + 0,5(3х -
1) > 3
х - 0,25х - 1 + 1,5х
– 0,5 > 3 х - 0,25х + 1,5х > 3+1+0,5
2,25х > 4,5
х > 2
x
Ответ: (2; +∞)
2
Решение:
Слайд 19
Решение:
2) х² + х < х(х - 5)
+ 2 х² + х < х2- 5х + 2
х² + х - х2 – 5х < 2
- 4х < 2
x
Ответ: ( ; +∞ )
Слайд 20Готовимся к ОГЭ
«Применение неравенств»
и их с
С помощью теоремы
Виета находим
корни
уравнения :
Найденные корни
поочерёдно подставляем
в данное неравенство
и проверяем какой из них
удовлетворяет условию.
Ответ: 4.
Слайд 21 2. Между какими двумя соседними целыми
числами находится число √32? К какому из
них оно ближе? ближе?Слайд 23Готовимся к ОГЭ
1) Задача. В типографию поступил для печати новый
учебник алгебры 8 класса. Но, к сожалению, в компьютере произошел
сбой, и одно из заданий стало выглядеть следующим образом: ''С помощью калькулятора найти значение выраженияпри следующих значениях переменных: 5; -2; -8,3; 10,63; -0,5; 3. Типографские корректоры заметили, что уже при х=-2 в приведенном выражении получаются странные вещи. Что происходит с выражением при х=-2? Как узнать, нет ли еще лишних чисел в данном упражнении?
2) При каких значениях переменной имеют смысл выражения :
А) ? Б) ?
Слайд 24Домашнее задание:
учебник: №855 (в, г), №847 (в, г),
№860
(б)
Рабочая тетрадь: стр 75 №8,9,12 (а)
Успехов
в учёбе!!! Слайд 25Кто круга от квадрата не может отличить,
Тому мы с математикой
советуем дружить
Нет лучше тренировки для вашего ума
Смекалки и сноровки прибавит
вам онаЛюбому, кто стремиться учиться лишь на «5»
Конечно, пригодится уменье рассуждать
«Величие человека – в его способности мыслить»
Блез Паскаль
Слайд 26 Реши задачи
I. Найдите наибольшее целое число, являющееся решением неравенства
2(х-3) - 1-3(х-2) - 4(х+1) > 0
0,2(2х+2) -
0,5(х-1) < 2III. Найдите наименьшее натуральное число, являющиеся решением неравенства
3х - 3 < 1,5х + 4
II. Найдите наименьшее целое число, являющееся решением неравенства
Слайд 27
Решение задачи I.
I. Найдите наибольшее целое число, являющееся
решением неравенства
2(х-3) - 1-3(х-2) - 4(х+1) > 0
2х
- 6 - 1- 3х + 6 - 4х - 4 > 0 -5х > 5
-5х - 5 > 0
х < -1
-1
-2
-3
x (-∞; -1)
Ответ: -2
х
Слайд 28
Решение задачи II.
0,2(2х+2) - 0,5(х-1) < 2
II. Найдите
наименьшее целое число, являющееся решением неравенства
0,4х + 0,4 -
0,5х +0,5 < 2 - 0,1х + 0,9 < 2
- 0,1х < 2 – 0,9
- 0,1х < 1,1
х > - 11
-11
-10
-9
x
x (-11; +∞)
Ответ: - 10.
Слайд 29 Решение задачи III.
III. Найдите наименьшее
натуральное число, являющиеся решением неравенства
3х - 3 < 1,5х +
43х - 1,5х < 4+3
1,5х < 7
х <
х
4
3
x (-∞; ),
Ответ: 1
2
1
натуральные решения 1; 2; 3;4.








 b (a ≥ b) или a" alt="Определение Запись вида a > b (a ≥ b) или a < b(a ≤ b ) называется">
b (a ≥ b) или a" alt="Определение Запись вида a > b (a ≥ b) или a < b(a ≤ b ) называется">






 " alt="1) х - 0,25(х + 4) + 0,5(3х - 1) > 3 х - 0,25х -">
" alt="1) х - 0,25(х + 4) + 0,5(3х - 1) > 3 х - 0,25х -">





























