Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
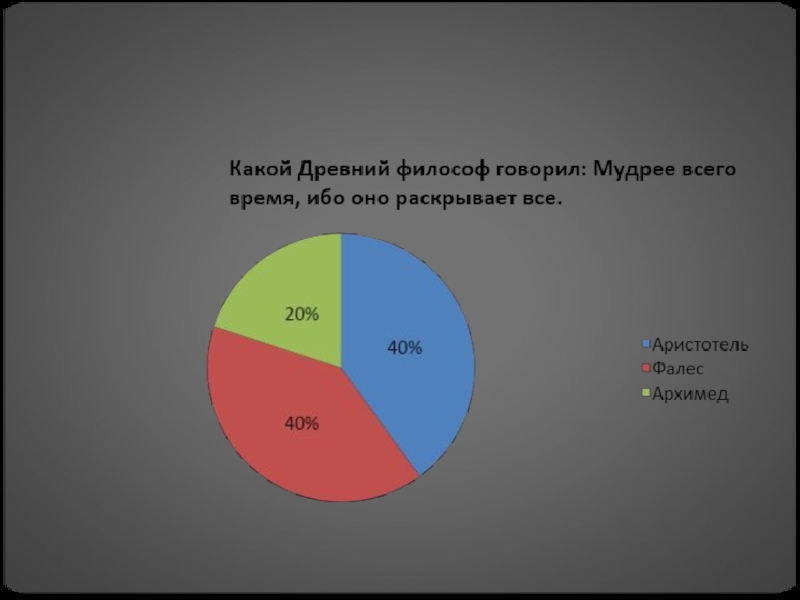
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по геометрии "Фалес и подобие треугольников"
Содержание
- 1. Презентация по геометрии "Фалес и подобие треугольников"
- 2. Тема проекта: Фалес и применение подобия треугольниковГеометрия
- 3. Цель проекта: Показать значение теорем ФАЛЕСА в
- 4. Задачи проектаПознакомиться с биографией Фалеса и значением
- 5. Проблемные вопросы проектаЗначение теорем Фалеса в современной
- 6. Фалес Милетский Дата рождения:640/624 до н. э.Дата
- 7. Биография Фалеса Кто же такой
- 8. Нахождение высоты египетской пирамидыПредставьте себе такую картину.
- 9. Достижениями Фалеса считаются: формулировка и доказательство
- 10. Теорема. В равнобедренном треугольнике углы при оcновании
- 11. Задача Фалеса Разделить данный отрезок AB на n равных частей.
- 12. Теорема ФалесаТеорема о параллельных прямых:Если на одной
- 13. Легенды о Фалесе Среди доказательств
- 14. Фалес научился определять расстояние от
- 15. Значение Фалеса в мировой истории развития науки.Эта
- 16. Применение подобия в архитектуре и культуре «Золотое
- 17. «Золотое сечение» в древней архитектуре.Даже сейчас, когда
- 18. «Золотое сечение» в живописиПортрет Моны Лизы привлекает
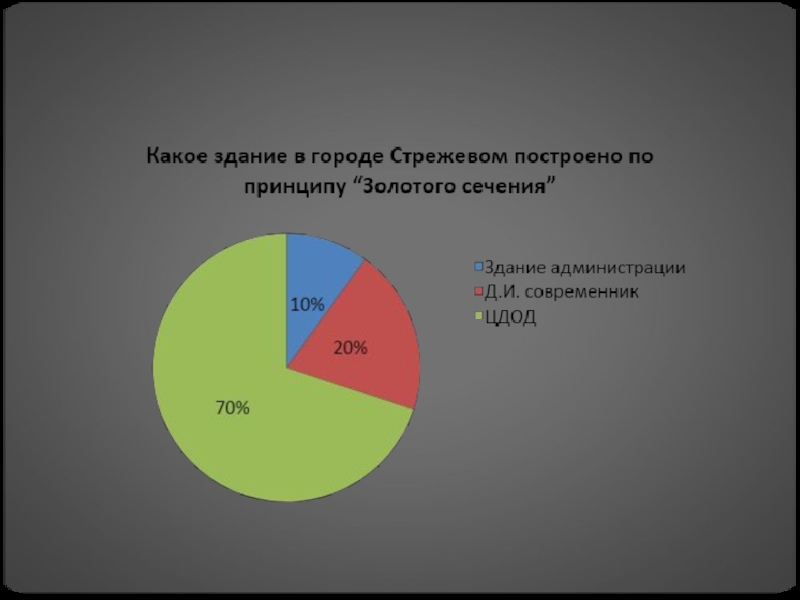
- 19. «Золотое сечение» в городе СтрежевомЕдинственноеархитектурное сооружение, построенное по принципу «золотого сечения» – здание администрации города.
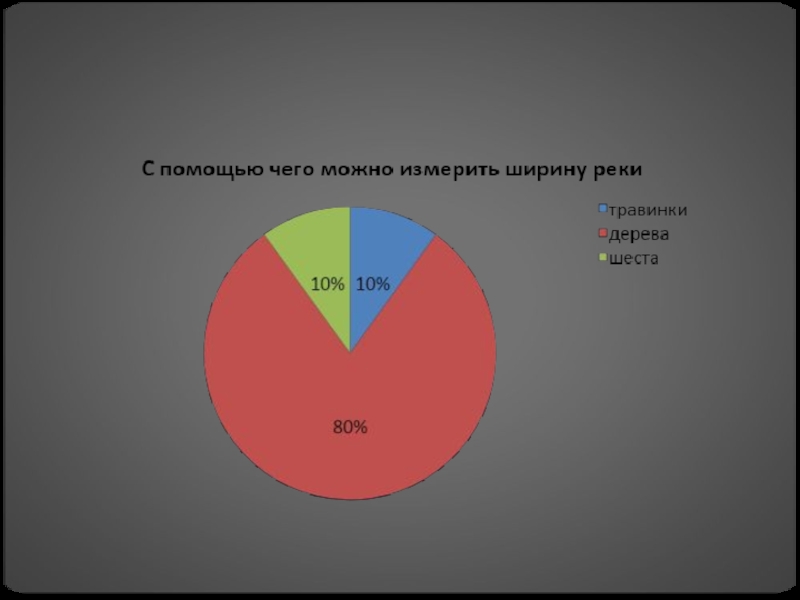
- 20. Определение ширины реки с помощью травинки.
- 21. Нахождение ширины Пасола в районе парковой зоны.Ширина
- 22. Определение высоты памятника первопроходцам в городе Стрежевом («Факел»)
- 23. Способ с помощью булавочного прибора.90м0.1м0.1мА1АВ1ВС1СДощечка с равнобедренным прямоугольным треугольником и тремя булавками в вершинах.
- 24. Наши расчётыА1 В1 С1 АВС по
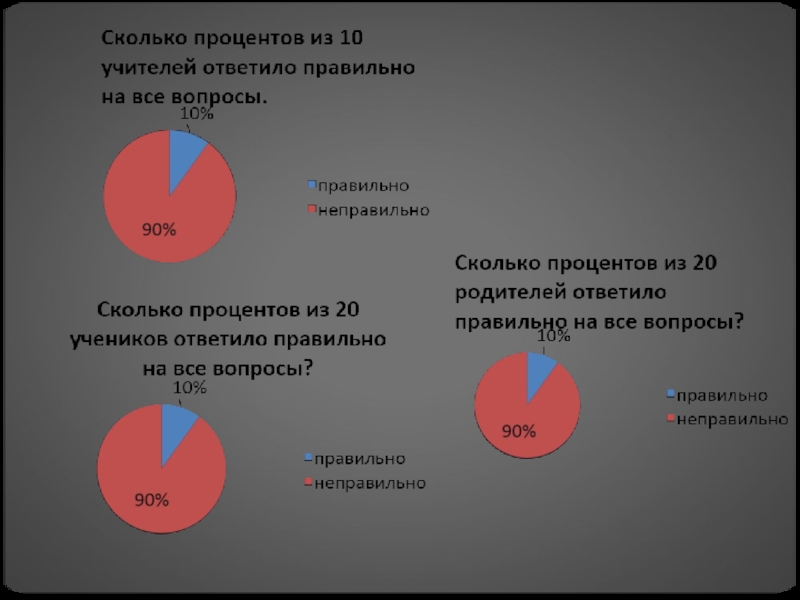
- 25. Социологический опрос: «Роль Фалеса и занимательные задачи геометрии»
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Рекламный буклет нашей исследовательской работы.
- 34. Слайд 34
- 35. Над проектом работали:
- 36. Саламатин АлександрМумбер Никита
- 37. Меньщиков ЕвгенийТомшин АртёмПатраков Виталий
- 38. Спасибо за внимание
- 39. Скачать презентанцию
Тема проекта: Фалес и применение подобия треугольниковГеометрия – это не просто наука о свойствахгеометрических фигур. Геометрия – это целый мир, который окружаетнас с самого рождения.
Слайды и текст этой презентации
Слайд 1Муниципальное бюджетное общеобразовательное учреждение Средняя общеобразовательная школа №4 го. Стрежевой
Проект по геометрии 8а класс
Слайд 2Тема проекта: Фалес и применение подобия треугольников
Геометрия – это не
просто наука о свойствах
геометрических фигур.
Геометрия – это целый мир,
который окружаетнас с самого рождения.
Слайд 3Цель проекта:
Показать значение теорем ФАЛЕСА в развитии науки и
культуры многих стран и народов мира, а так же рассмотреть
практическое применение подобия треугольников в жизнедеятельности человека.Слайд 4Задачи проекта
Познакомиться с биографией Фалеса и значением его теорем.
Рассмотреть применения
подобия на практике и практических задачах.
Изготовить «булавочного прибора».
Создать рекламного буклета.
Провести
опрос по теме «Значение Фалеса в мировой истории»Развивать познавательный интерес методами геометрии.
Слайд 5Проблемные вопросы проекта
Значение теорем Фалеса в современной истории математики.
Подобие треугольников
в природе и жизни человека.
Изучение интеллектуального уровня людей в вопросах
геометрии.Слайд 6Фалес Милетский
Дата рождения:640/624 до н. э.
Дата смерти:548/545 до н. э.
Место
смерти:Милет
Школа/традиция: Милетская школа
Направление: Западная Философия
Период: Древнегреческая философия
Основные интересы: философия, математика
Слайд 7Биография Фалеса
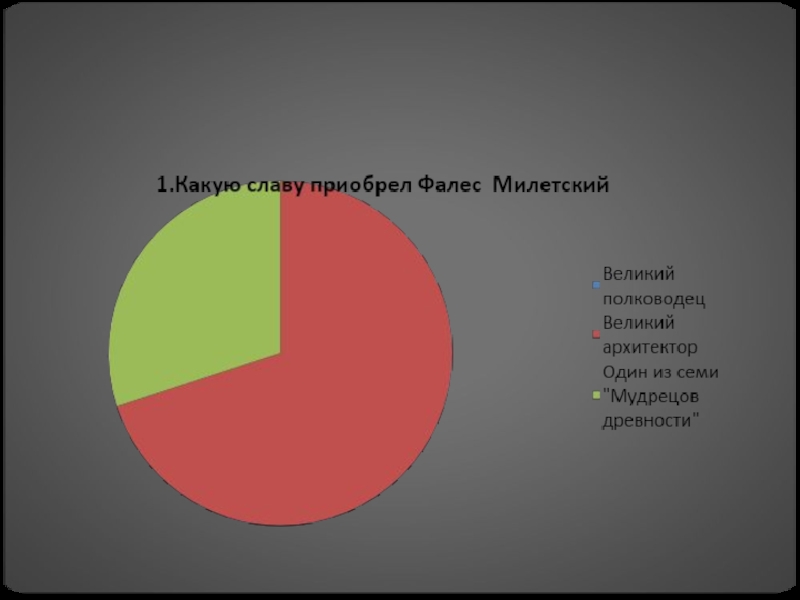
Кто же такой этот Фалес Милетский? Человек,
который обрел славу одного из «семи мудрецов» древности. Фалес Милетский
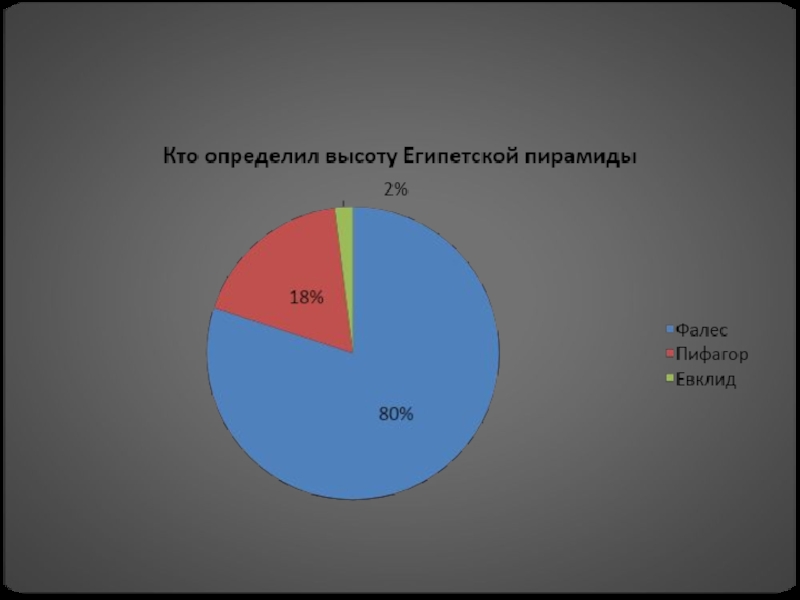
– древнегреческий философ, который отличился успехами в области астрономии, а также математики и физики. Годы его жизни были установлены только приблизительно: 625-645 гг до н.э.Слайд 8Нахождение высоты египетской пирамиды
Представьте себе такую картину. 600г. до н.э.
Египет. Перед вами огромнейшая египетская пирамида. Чтобы удивить фараона и
остаться у него в фаворитах, вам нужно измерить высоту этой пирамиды. В распоряжении у вас… ничего. Можно пасть в отчаяние, а можно поступить, как Фалес Милетский: использовать теорему подобия треугольников. Да, оказывается, все достаточно просто. Фалес Милетский подождал, пока длина его тени и его рост совпадут, а затем с помощью теоремы о подобии треугольников нашел длину тени пирамиды, которая, соответственно, была равна тени, отбрасываемой пирамидой.Слайд 9Достижениями Фалеса считаются:
формулировка и доказательство следующих теорем:
вертикальные углы равны;
равными
треугольниками признаются те, у которых сторона и два прилегающих угла
соответственно равны;углы при основании равнобедренного треугольника равны;
диаметр делит круг пополам;
вписанный угол, опирающийся на диаметр, является прямым.
Слайд 10Теорема. В равнобедренном треугольнике углы при оcновании равны.
Доказательство.
Рассмотрим равнобедренный треугольник
АВС с основанием ВС и докажем, что В = С.
Пусть АD — биссектриса треугольника АВС.Треугольники АВD и АСD равны по первому признаку равенства треугольников (АВ = АС по условию, АD — общая сторона, 1 = 2, так как AD — биссектриса). В равных треугольниках против равных сторон лежат равные углы, поэтому В = С. Теорема доказана.
Слайд 11Задача Фалеса
Разделить данный отрезок AB на n равных частей.
Построение. Пусть [AB] – данный
отрезок. Проведем из точки A луч a, не содержащий отрезок AB. Отложим от точки A на
построенном луче равные отрезки: AA1, A1A2, ... , An – 1An. Соединим точки Anи B. Проведем через точки A1, A2, ... , An – 1 прямые, параллельные прямой AnB. Они пересекают отрезок AB в точках B1, B2, ... , Bn – 1. Отрезки AB1, B1B2, ... , Bn – 1B – искомые отрезки.Слайд 12Теорема Фалеса
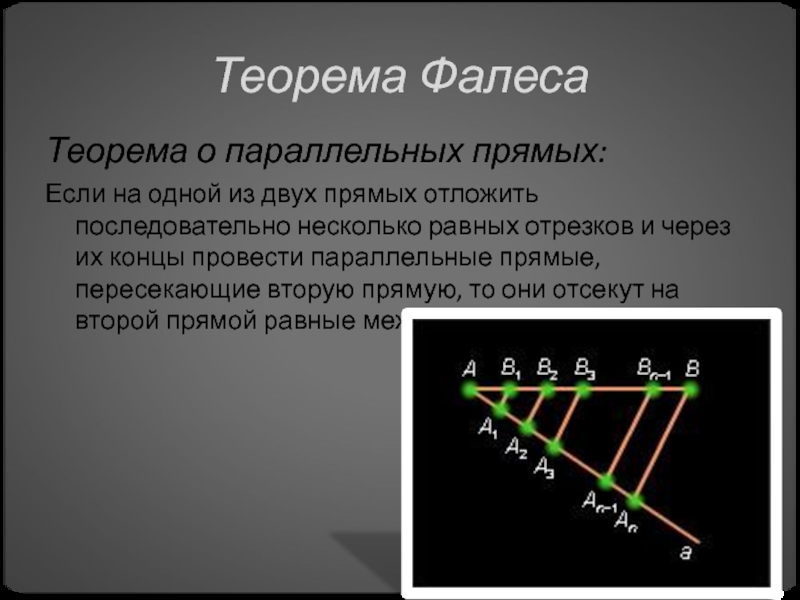
Теорема о параллельных прямых:
Если на одной из двух прямых
отложить последовательно несколько равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.Слайд 13Легенды о Фалесе
Среди доказательств знания Фалесом астрономии
можно привести следующий пример. 28 мая 585 г до н.э. предсказание
Милетским солнечного затмения помогло прекратить длившуюся уже 6 лет войну между Лидией и Мидией. Это явление настолько испугало мидян, что они согласились на невыгодные для себя условия заключения мира с лидийцами.Слайд 14 Фалес научился определять расстояние от берега до корабля,
для чего использовал подобие треугольников. В основе этого способа лежит
теорема, названная впоследствии теоремой Фалеса. Далеко от берега стоял на якоре корабль. Фалес сумел измерить расстояние от берега до корабля. В точности, как он это сделал, мы не знаем: его труды до нас не дошли.Слайд 15Значение Фалеса в мировой истории развития науки.
Эта гробница мала, но
слава над ней необъятна.
В ней перед тобою сокрыт многоразумный Фалес.
Слайд 16Применение подобия в архитектуре и культуре «Золотое сечение»
Принцип золотого сечения
– высшее
проявление структурного и функцио-
нального совершенства целого и его
частей в
искусстве, науке, технике иприроде.
Золотое сечение – это такое пропорциональное деление отрезка
на неравные части, при котором весь отрезок так относится к большей
части, как сама большая часть относится к меньшей; или другими
словами, меньший отрезок так относится к большему, как больший
ко всему.
Пропорция отношений длин сторон любой фигуры равная, 1.6 называется золотым.
Слайд 17«Золотое сечение» в древней архитектуре.
Даже сейчас, когда храм стоит на
развалинах, это одно из самых
красивых сооружений мира. Он построен
в эпоху расцвета древнегреческой математики. И его красота основана на строгих математических законах. Если мы опишем около фасада Парфенона прямоугольник, то окажется, что его стороны образуют золотое сечение. Такой прямоугольник назвали «золотым прямоугольником»Слайд 18«Золотое сечение» в живописи
Портрет Моны Лизы привлекает тем, что композиция
рисунка
построена на «золотых треугольниках (точнее на треугольниках,
являющихся кусками
правильного звездчатого пятиугольника). Слайд 19«Золотое сечение» в городе Стрежевом
Единственное
архитектурное сооружение,
построенное
по принципу
«золотого сечения» – здание администрации города.
Слайд 20Определение ширины реки с помощью травинки.
Описание
способа:
Сорвите травинку. Выберите на противоположном берегу два предмета и встаньте
к ним лицом. Руки с травинкой вытяните вперед и с ее помощью отмерьте расстояние между предметами, глядя на них одним глазом. Затем сложите травинку вдвое и потихоньку отходите от берега реки.Остановитесь, когда сложенная пополам травинка не закроет расстояние между предметами. Вставьте в этом месте ветку, замерьте пройденное вами расстояние от берега реки до ветки и переведите его в метры. Получили расстояние, которое равно ширине реки.
Слайд 21Нахождение ширины Пасола в районе парковой зоны.
Ширина реки Пасол в
том месте, где мы замеряли, была 12.5м.
Мы подошли
к краю реки и нашли на другом берегу 2неподвижные точки (2 куста). Взяв травинку ,мы держали её так что бы её края касались 2 кустов. Сложив травинку, начали отходить до тех пор, пока её края опять не коснулись 2 кустов.
При измерении расстояния пройденного пути и у нас получилось 12.5 м.
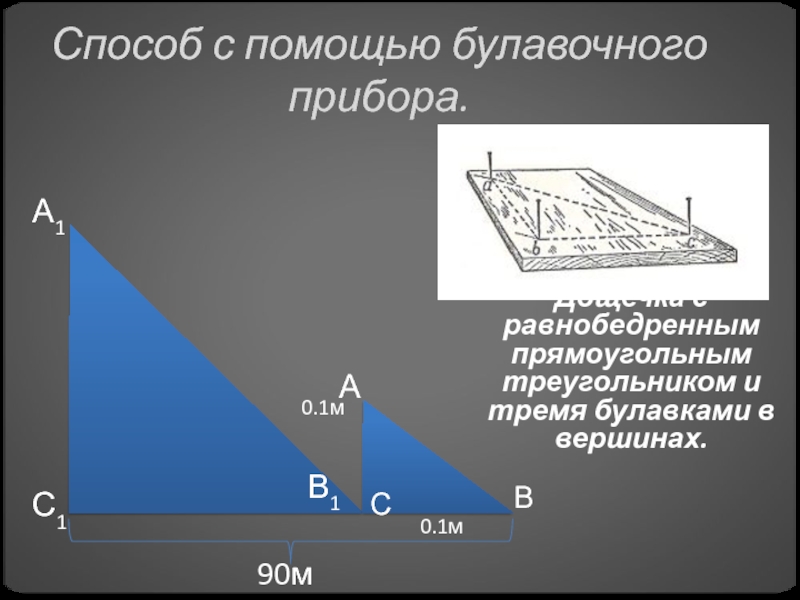
Слайд 23Способ с помощью булавочного прибора.
90м
0.1м
0.1м
А1
А
В1
В
С1
С
Дощечка с равнобедренным прямоугольным треугольником и
тремя булавками в вершинах.
Слайд 24Наши расчёты
А1 В1 С1 АВС по первому признаку подобия.
А1С1
= 0.190:0.1 = 90см (высота шестой части памятника)
906 = 5.4м
(высота памятник, а не учитывая рост человека)5.4 + 1.7 = 7.1м (высота памятника без высоты ступеней(1.7 – рост человека))
7.1 – 0.5 = 6.6м (высота памятника «Факел»)










![Презентация по геометрии Задача Фалеса Разделить данный отрезок AB на n равных частей. Построение. Пусть [AB] – данный отрезок. Проведем из точки A луч a, не содержащий отрезок AB.](/img/thumbs/43570970f32237fbfb8c072bda49458e-800x.jpg)