Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для занятия элективного курса "Схема Горнера и её применение"
Содержание
- 1. Презентация для занятия элективного курса "Схема Горнера и её применение"
- 2. Разложение многочлена на множители.P(x)= 3x3+2x2_ x-4 –многочленP(1)=3·13+2·12-1-4=0
- 3. Теорема БезуБезу Этьен (Bezout Etienne)
- 4. Таким образом, если а - корень многочлена,
- 5. Разделим многочлен Р(х) на двучлен х-а, где
- 6. Уильямс Джордж ГорнерГорнер Вильямc Джордж (1786-22.9.1837) -
- 7. Вычисление значений многочленаНайдём значение f(x) = x3
- 8. Поиск целых корней многочленаИспользуя схему Горнера, найдём
- 9. Решение алгебраических уравненийРешить уравнение : 4x5+4x4-13x3-6x2+9x+2=01. Найдём
- 10. Самостоятельная работаВариант 1Вариант 2Решить уравнение: х3-4х2+х+6=0Решить уравнение: х3-3х2+6х-4=0
- 11. Список используемых ресурсов.Методика преподавания темы «Схема Горнера,
- 12. Скачать презентанцию
Разложение многочлена на множители.P(x)= 3x3+2x2_ x-4 –многочленP(1)=3·13+2·12-1-4=0 => X=1 – кореньПредставим P(x) в виде: 3x3+2x2_ x-4 = 3x2 (x-1) + 5x2-x-4 =
Слайды и текст этой презентации
Слайд 1Схема ГОРНЕРА
и её применения.
Разработка учителя математики
МОУ СОШ №3 г. Хвалынска Грибановой Т.А.
Слайд 2Разложение многочлена на множители.
P(x)= 3x3+2x2_ x-4 –многочлен
P(1)=3·13+2·12-1-4=0 => X=1 –
корень
Представим P(x) в виде:
3x3+2x2_ x-4 = 3x2 (x-1) +
5x2-x-4 =
3x3-3x2
=3x2(x-1)+ 5x (x-1)+ 4x-4 =
5x2-5x
= 3x2(x-1)+5x(x-1)+4(x-1)+0 = (x-1)(3x2+5x+4). Заметим, что остаток 0 равен значению Р(1)
X=1 – кореньПредставим" alt="Разложение многочлена на множители.P(x)= 3x3+2x2_ x-4 –многочленP(1)=3·13+2·12-1-4=0 => X=1 – кореньПредставим P(x) в виде: 3x3+2x2_ x-4">Слайд 3Теорема Безу
Безу Этьен
(Bezout Etienne)
Остаток от деления многочлена
Р(х) на двучлен х-а равен значению этого многочлена при х=а,
т.е. Р(а)=R.Следствие
Для того, чтобы многочлен Р(х) делился на двучлен х-а, необходимо и достаточно, чтобы при х=а он обращался в нуль.
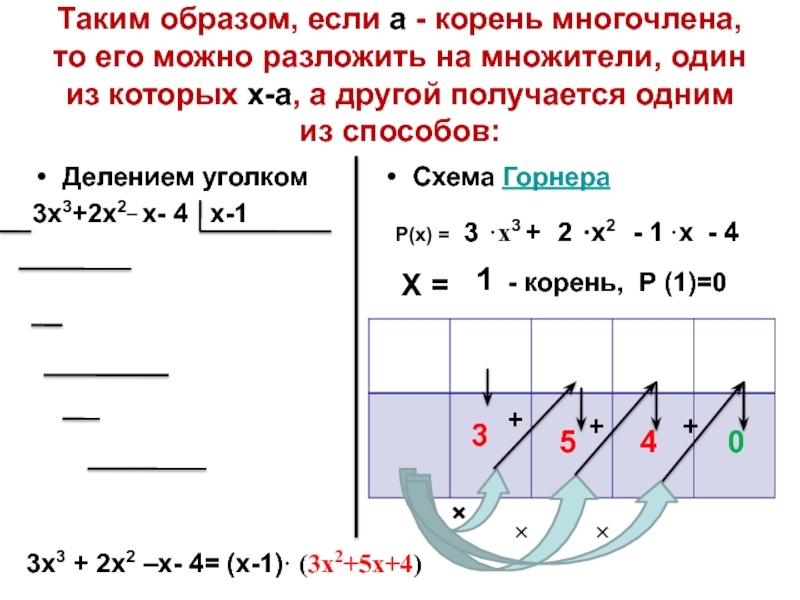
Слайд 4Таким образом, если а - корень многочлена, то его можно
разложить на множители, один из которых х-а, а другой получается
одним из способов:Делением уголком
3x3+2x2_ x- 4 x-1
Схема Горнера
P(x) =
3
·x3 +
2
·x2
- 1
·x
- 4
3
2
- 1
- 4
X =
1
1
- корень, Р (1)=0
3
5
4
0
×
×
×
+
+
+
3x3 + 2x2 –x- 4= (x-1)· (3x2+5x+4)
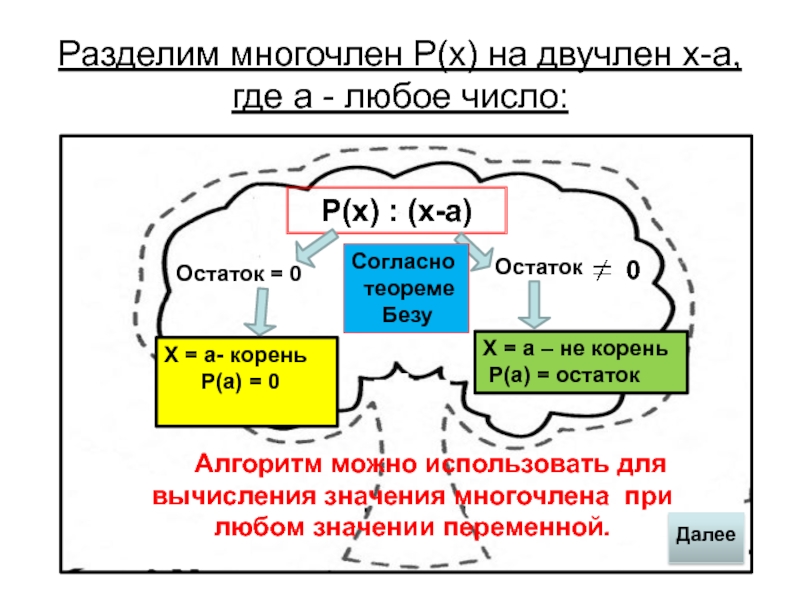
Слайд 5Разделим многочлен Р(х) на двучлен х-а, где а - любое
число:
Р(х) : (х-а)
Остаток = 0
Остаток
0
Х = а- корень
Р(а) = 0Х = а – не корень
Р(а) = остаток
Согласно
теореме
Безу
Алгоритм можно использовать для вычисления значения многочлена при любом значении переменной.
Слайд 6Уильямс Джордж Горнер
Горнер Вильямc Джордж (1786-22.9.1837) - английский математик. Окончил
Бристольскую школу (1800). С 1800 преподавал там же, в 1809-1837
гг. работал в школах Бата.Исследования относятся к теории алгебраических уравнений. Разработал (1819) способ приближенного решения уравнений любой степени, который несколько раньше предложил П. Руффини(этот способ был известен китайцам еще в XIII в.). Ввел существенно важный для алгебры способ деления многочлена на двучлен, названных схемой Руфини-Горнера.
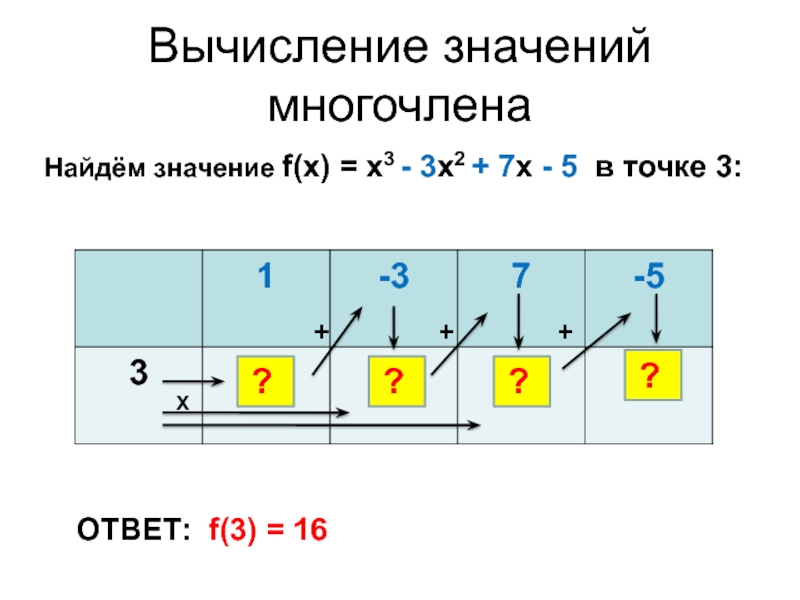
Слайд 7Вычисление значений многочлена
Найдём значение f(x) = x3 - 3x2 +
7x - 5 в точке 3:
ОТВЕТ: f(3) = 16
Х
+
+
+
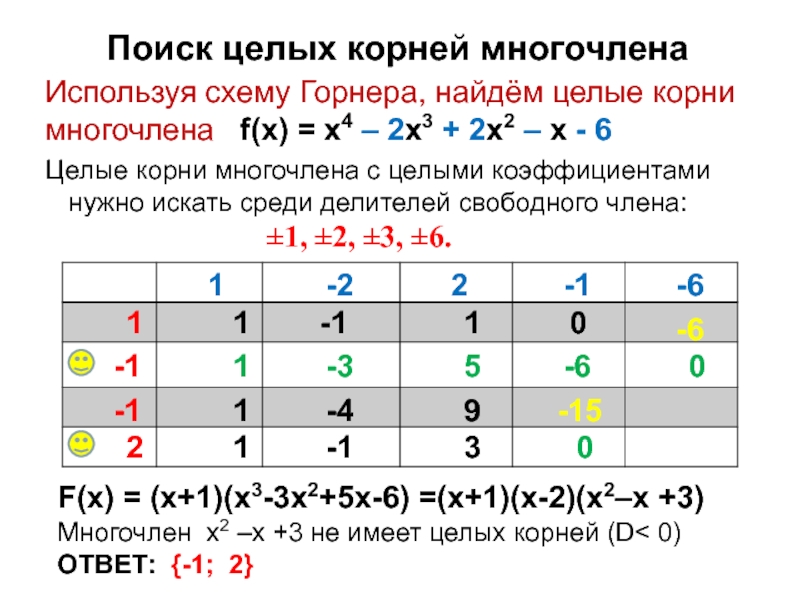
Слайд 8Поиск целых корней многочлена
Используя схему Горнера, найдём целые корни многочлена
f(x) = x4 – 2x3 + 2x2 – x
- 6Целые корни многочлена с целыми коэффициентами нужно искать среди делителей свободного члена:
±1, ±2, ±3, ±6.
F(x) = (x+1)(x3-3x2+5x-6) =(x+1)(x-2)(x2–x +3)
Многочлен x2 –x +3 не имеет целых корней (D< 0) ОТВЕТ: {-1; 2}
1
-1
-1
2
1
1
1
1
-1
-3
-4
-1
1
5
9
3
0
-6
-15
0
-6
0
1
-2
2
-1
-6
Слайд 9Решение алгебраических уравнений
Решить уравнение : 4x5+4x4-13x3-6x2+9x+2=0
1. Найдём целый корень
уравнения из делителей свободного члена 2: ±1,±2
ПОДСКАЗКИ
2. Найдём целый корень
второго многочлена из делителей его свободного члена 1: ±1.4x5+4x4-13x3-6x2+9x+2=
(x+2)(4x4-4x3-5x2+4+1)
4x5+4x4-13x3-6x2+9x+2=
(x+2)(x-1)(4x3-5x-1)
3. Найдём целый корень третьего многочлена.
4x5+4x4-13x3-6x2+9x+2=(x+2)(x-1)(x+1)(4x2-4x-1)
4x2-4x-1=0; X1=0,5(1-√2); x2=0,5(1+√2)
ОТВЕТ: { -2; 1; -1; 0,5(1-√2); 0,5(1+√2)}
Слайд 10Самостоятельная работа
Вариант 1
Вариант 2
Решить уравнение:
х3-4х2+х+6=0
Решить уравнение:
х3-3х2+6х-4=0
Слайд 11Список используемых ресурсов.
Методика преподавания темы «Схема Горнера, теорема Безу и
деление уголком». Из копилки приемов репетитора по математике Колпакова А.Н.,
2010г. http://www.ankolpakov.ru/«Схема Горнера » Е.А.Максименко, Южный федеральный университет, 2007 г.
Исторические сведения: ВИКИПЕДИЯ
