Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи с параметрами в системе ЕГЭ и методика их решения
Содержание
- 1. Задачи с параметрами в системе ЕГЭ и методика их решения
- 2. Цель: формирование общих методов решения уравнений
- 3. Теоретические сведения Определение 1 Уравнение вида
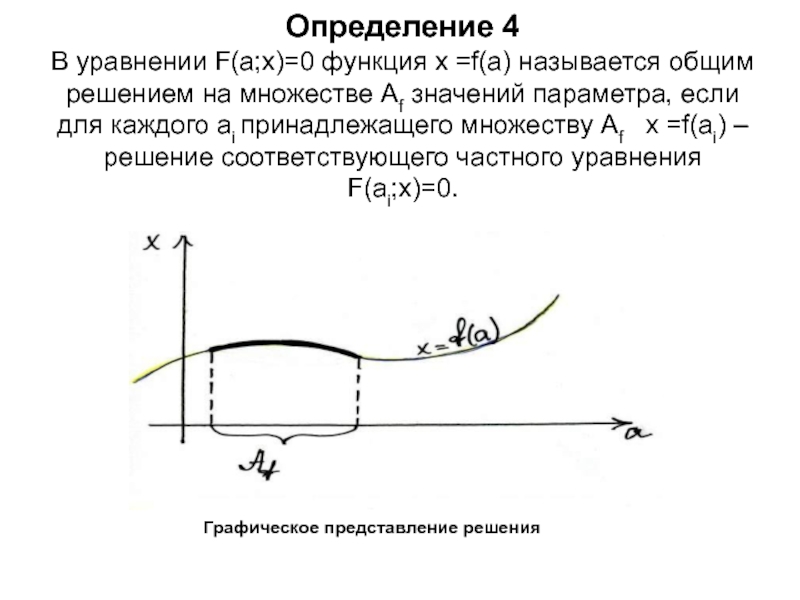
- 4. Определение 4 В уравнении F(a;x)=0 функция
- 5. Общий метод решения линейных уравнений с параметром:Найдём
- 6. Общий метод решения квадратных уравнений с параметром:Находим
- 7. Общий метод решения линейных уравнений функционально-графическим методом:В
- 8. Применение функционально-графического метода решения уравненийС5. ЕГЭ. Найдите
- 9. Решение: 1.Решим уравнение (2,5 - а)х3-2х2 +
- 10. Число общих точек пересечения линий х2 +
- 11. Модель решений:Ответ: 2,5; 8; 10.
- 12. Методика формирования общего метода решений уравнений и
- 13. СПАСИБО ЗА ВНИМАНИЕ
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Цель: формирование общих методов решения уравнений и неравенств, содержащих параметр,
в классах линейных уравнений (неравенств) и уравнений не выше второй
степени
Задачи:
1.ввести понятия уравнений(неравенств) с параметром, определить, что значит решить уравнение, содержащие параметр;
2.установить общий метод решения линейных уравнений(неравенств) и научиться его применять при решении конкурсных задач и задач ЕГЭ;
3.установить общий метод решения уравнений не выше 2 степени и использовать его при подготовке учащихся к ЕГЭ по математике;
Слайд 3Теоретические сведения
Определение 1
Уравнение вида F(a,x)=0 с двумя переменными
х и а, называется уравнением с параметром а и переменной
х, если для каждого значения переменной а = аi необходимо исследовать соответствующие частные уравнения F(ai,x)=0.Определение 2
Уравнение вида f(a)x+g(a)=0, где f(a) и g(a) – любые выражения с параметром а и х – переменная, называется линейным уравнением стандартного вида.
Определение 3
Уравнение вида f(a)x2 +g(a)x+h(a)=0 c параметром а и переменной х называется уравнением стандартного вида не выше второй степени
Слайд 4 Определение 4 В уравнении F(a;x)=0 функция х =f(a) называется общим решением
на множестве Af значений параметра, если для каждого ai принадлежащего
множеству Аf х =f(ai) – решение соответствующего частного уравнения F(ai;x)=0.Графическое представление решения
Слайд 5Общий метод решения линейных уравнений с параметром:
Найдём все значения, где
параметр не определён и запишем ОДЗП.
Выполним равносильные преобразования и запишем
уравнение в виде f(a)x+g(a)=0, который является стандартным для данного класса уравнений.Найдём КЗП, решив уравнение f(a)=0
Для каждого контрольного значения параметра решим соответствующее частное уравнение.
Находим общее решение уравнения x=-g(a)/f(a) для всех значений а, кроме КЗП.
При необходимости строим модель общих решений и записываем ответ.
Слайд 6Общий метод решения квадратных уравнений с параметром:
Находим КЗП, для которых
соответствующие частные уравнения не определены, записываем ОДЗП.
На ОДЗП исходное уравнение
при помощи равносильных преобразований приводим к стандартному виду f(a)x2+g(a)x+h(a)=0Выделяем множество КЗП, где f(a)=0 и для каждого КЗП решаем соответствующее частное уравнение, если f(a)=0 имеет конечное множество решений.
Выделяем КЗП, для которых Д=g(a)2 - 4f(a)h(a) обращается в нуль. Соответствующие частные уравнения имеют двукратный корень x= -g(a)/2f(a)
На каждом промежутке ОДЗП определяем знак дискриминанта и решаем частные уравнения.
Составляем модель решений.
Записываем ответ.
Слайд 7Общий метод решения линейных уравнений функционально-графическим методом:
В уравнении находим ОДЗП.
На
ОДЗП уравнение приведем к виду
f(a)x + g(a)=F(x).Введем функции:
а) линейную с параметром вида y=f(a)x + g(a) - бесконечное множество частных функций;
б) y=F(x) - функция со строго фиксированным графиком, где F(x)=kx+l
Из уравнения f(ai)=k находи КЗП, для которого график частной линейной функции y=f(ai)x+g(ai) параллелен графику y=kx+l.
Для остальных f(ai) ≠ k, для частных линейных функций y=f(ai)x+g(ai) и y=F(x) находим число решений уравнения.
Записываем ответ.
Слайд 8 Применение функционально-графического метода решения уравнений
С5. ЕГЭ.
Найдите значения параметра а,
при которых количество корней уравнения (2,5 – а)х3 -2х2 +
х =0 равно количеству общих точек линий х2 + у2 = а и у = 3 -|х-1|Слайд 9Решение:
1.Решим уравнение (2,5 - а)х3-2х2 + х =0 аналитическим методом.
х((2,5
– а)х2 – 2х + 1) =0 х = 0 или
(2,5 – а)х2 – 2х + 1 =0 (1)Решим уравнение (1). КЗП: а = 2,5; Для остальных значений а, не равных 2,5, исследуем уравнение (1). В зависимости от знака дискриминанта Д1 = а – 1,5 получим:
1 корень-
2 корня-
3 корня -
Слайд 10Число общих точек пересечения линий х2 + у2 = а
и
у = 3 - |х-1| найдем графически.
1)
х2 + у2 = а – это уравнение окружностей с центром в начале координат и а=R22) у = 3 - |х-1| - «уголок»
Заметим, что окружность будет касаться «уголка», если а = 2;8;10.
Таким образом:
1 точка –
2 точки –
3 точки –
4 точки –
Точек пересечения нет -
Слайд 12Методика формирования общего метода решений уравнений и неравенств с параметром
I.
Рассмотреть конкретный пример и выделить все закономерности действия в решении
уравнения (неравенства) с параметромII. Выделить общий метод решения
III. Закрепить выделенный метод решения, фиксируя действия в общей схеме и проговаривая каждый этап
IV. Представить схему общего метода решения (как правило, учащиеся выполняют это самостоятельно).