Слайд 1ТЕОРЕМА ПИФАГОРА И ЕЁ ПРИМЕНЕНИЕ В КУРСЕ ГЕОМЕТРИИ
К наиболее важным
и замечательным теоремам элементарной евклидовой геометрии относится теорема Пифагора. Геометрический
факт, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов, был известен задолго до Пифагора. Так, египетские землемеры ещё около 2000 лет до н. э. фактически пользовались обратной теоремой Пифагора, при построении прямых углов обращаясь к треугольнику со сторонами 3, 4, 5.
Значение этой темы выходит далеко за рамки элементарной геометрии. Вот почему в средней школе изучению теоремы Пифагора уделяется много внимания. Изучающему геометрию важно не только знать зависимость между отрезками, являющимися сторонами прямоугольного треугольника, но и обратно: знать аналитический критерий перпендикулярности двух отрезков (или двух прямых), когда эти отрезки (или прямые) произвольно лежать на плоскости или в пространстве.
Слайд 2БИОГРАФИЯ ПИФАГОРА
Великий ученый Пифагор родился около 570 г. до н.э.
на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным
камням. Имя же матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид же был философом и считался основателем италийской школы философии. Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной советовал видеть своего первого и главного учителя. Но как бы то ни было, неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и сделал.

Слайд 3
В 548 г. до н.э. Пифагор прибыл в Навкратис –
самосскую колонию, где было у кого найти кров и пищу.
Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принцыпов достойны подражания и сейчас.
...Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.

Слайд 4ПИФАГОРЕЙЦЫ
Союз пифагорейцев был тайным. Эмблемой или опознавательным знаком союза являлась
пентаграмма - пятиконечная звезда. Пентаграмме присваивалась способность защищать человека от
злых духов.
пифагорейцы
Слайд 5ИСТОРИЯ ТЕОРЕМЫ ПИФАГОРА
Исторический обзор начнем с древнего Китая. Здесь особое
внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится
о пифагоровом треугольнике со сторонами 3, 4 и 5: "Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Кантор (крупнейший немецкий историк математики) считает, что равенство
3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
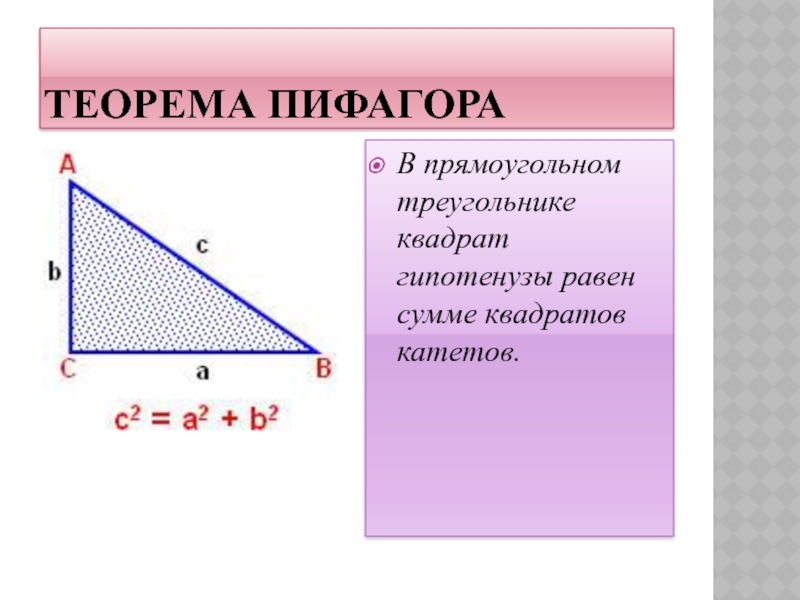
Слайд 6ТЕОРЕМА ПИФАГОРА
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 7
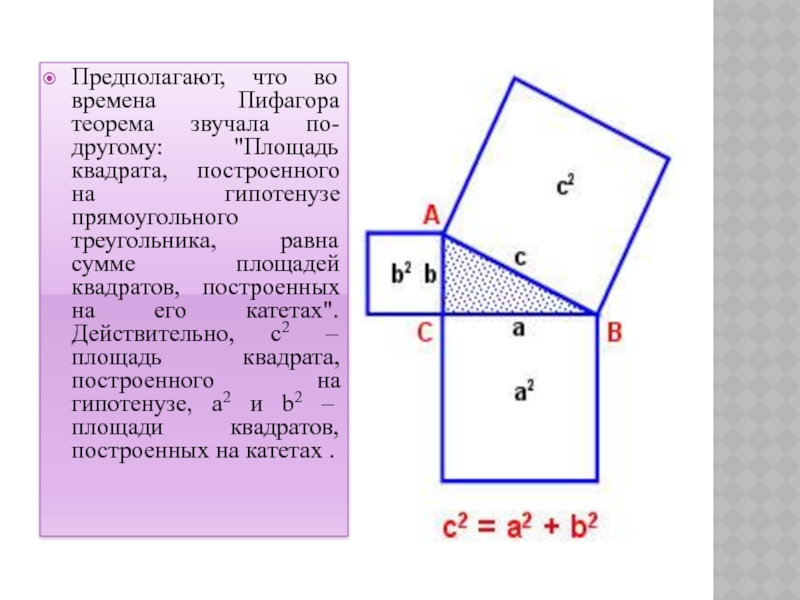
Предполагают, что во времена Пифагора теорема звучала по-другому: "Площадь квадрата,
построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных
на его катетах". Действительно, с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов, построенных на катетах .
Слайд 8
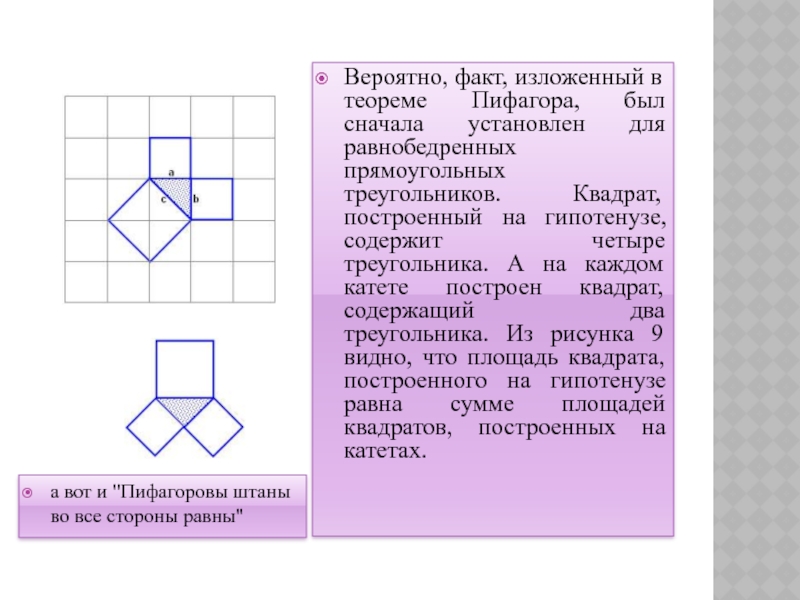
а вот и "Пифагоровы штаны во все стороны равны"
Вероятно,
факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных
прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка 9 видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.
Слайд 9А ВОТ ШАРЖИ ,КОТОРЫЕ ПРИДУМЫВАЛИ УЧАЩИЕСЯ СРЕДНИХ ВЕКОВ ПРИ ИЗУЧЕНИИ
ТЕОРЕМЫ
Слайд 10ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ В СОВРЕМЕННОЙ ФОРМУЛИРОВКЕ
Начертим треугольник АВС с прямым углом
С.
Д а н о: Δ АВС, ∠ С = 90°.
Д
о к а з а т ь: АВ2 = АС2 + ВС2.
Д о к а з а т е л ь с т в о:
Проведём высоту CD из вершины прямого угла С.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе, поэтому в Δ ACD cos A = AD / AC,
а в Δ АВС cos А = AC / AB . Так как равны левые части этих равенств, то равны и правые, следовательно,
AD / AC = AC / AB.
Отсюда, по свойству пропорции, получаем: АС2 = AD · АВ. (1)
Аналогично, в Δ ВCD cos В = BD / BC,
а в Δ АВС cos В = BC / AB.
Так как равны левые части этих равенств, то равны и правые, следовательно, BD / BC = BC / AB. Отсюда, по свойству пропорции, получаем: ВС2 = ВD · АВ. (2)
Сложим почленно равенства (1) и (2), и вынесем общий множитель за скобки:
АС2 + ВС2 = AD · AB + BD · AB = AB · (AD + BD).
Так как AD + BD = АВ, то
АС2 + ВС2 = AB · AB = AB2.
Получили, что АВ2 = АС2 + ВС2.
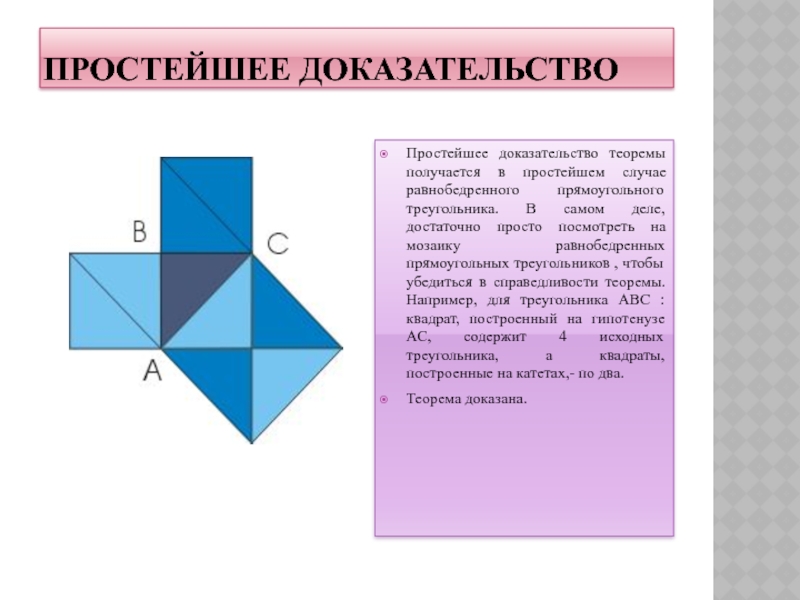
Слайд 11ПРОСТЕЙШЕЕ ДОКАЗАТЕЛЬСТВО
Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного
треугольника. В самом деле, достаточно просто посмотреть на мозаику равнобедренных
прямоугольных треугольников , чтобы убедиться в справедливости теоремы. Например, для треугольника ABC : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.
Теорема доказана.
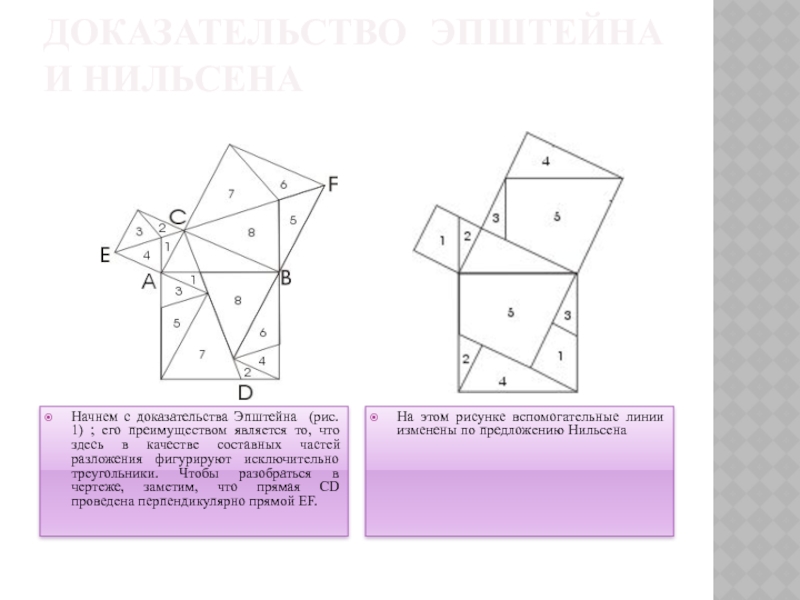
Слайд 12ДОКАЗАТЕЛЬСТВО ЭПШТЕЙНА И НИЛЬСЕНА
Начнем с доказательства Эпштейна (рис. 1) ;
его преимуществом является то, что здесь в качестве составных частей
разложения фигурируют исключительно треугольники. Чтобы разобраться в чертеже, заметим, что прямая CD проведена перпендикулярно прямой EF.
На этом рисунке вспомогательные линии изменены по предложению Нильсена
Слайд 13ТЕОРЕМА ПИФАГОРА В СТИХАХ
Итак, Если дан нам треугольник
И притом с
прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму
степеней находим
И таким простым путём
К результату мы придём.
Ч. т. д.
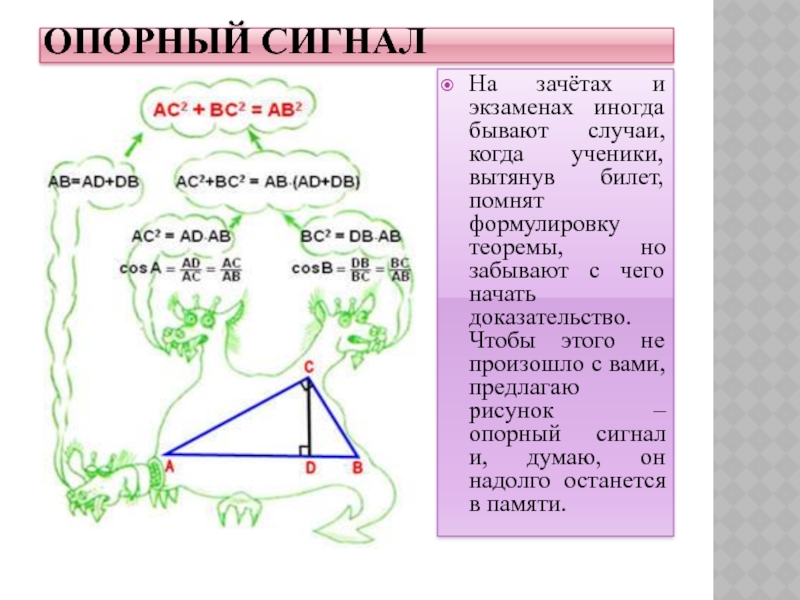
Слайд 14ОПОРНЫЙ СИГНАЛ
На зачётах и экзаменах иногда бывают случаи, когда ученики,
вытянув билет, помнят формулировку теоремы, но забывают с чего начать
доказательство. Чтобы этого не произошло с вами, предлагаю рисунок – опорный сигнал и, думаю, он надолго останется в памяти.
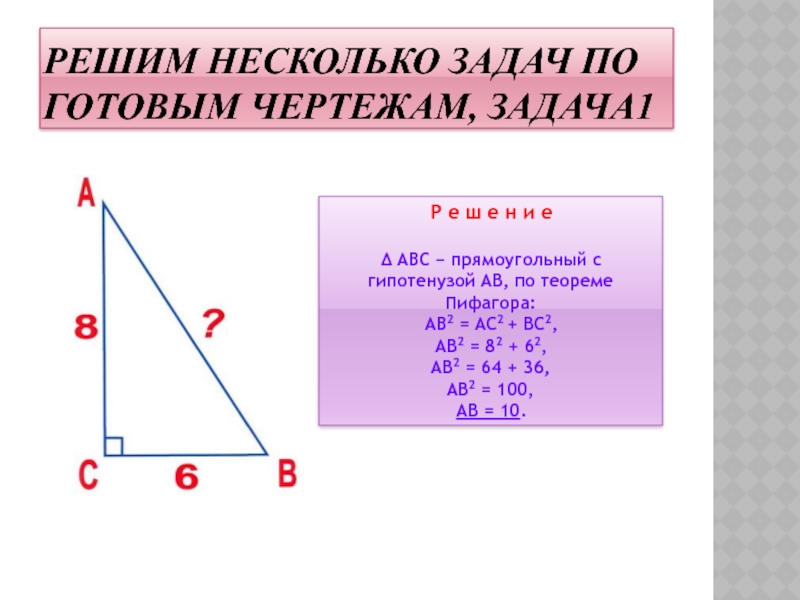
Слайд 15РЕШИМ НЕСКОЛЬКО ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ, ЗАДАЧА1
Р е ш е
н и е
Δ АВС − прямоугольный с гипотенузой АВ, по теореме Пифагора:
АВ2 = АС2 + ВС2,
АВ2 = 82 + 62, АВ2 = 64 + 36, АВ2 = 100,
АВ = 10.
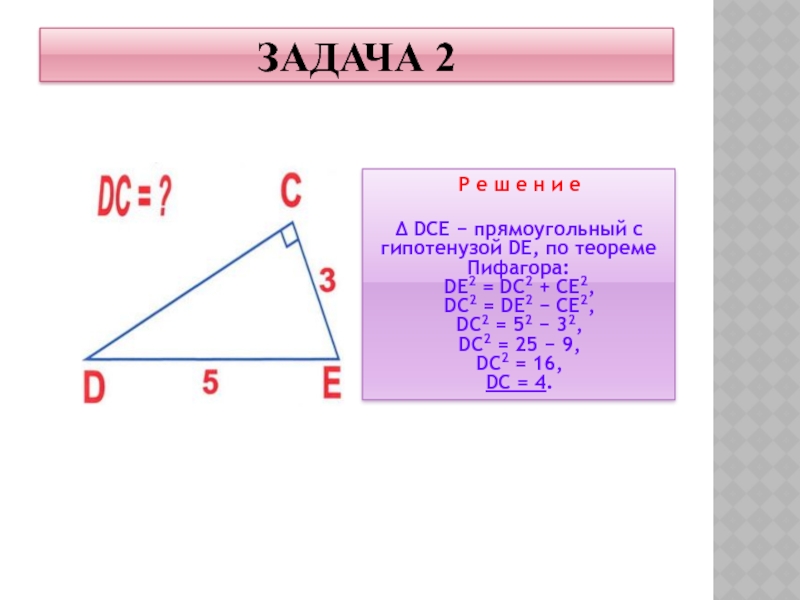
Слайд 16ЗАДАЧА 2
Р е ш е н и е
Δ DCE −
прямоугольный с гипотенузой DE, по теореме Пифагора:
DE2 = DС2
+ CE2,
DC2 = DE2 − CE2,
DC2 = 52 − 32,
DC2 = 25 − 9,
DC2 = 16,
DC = 4.
Слайд 17ЗАДАЧА 3
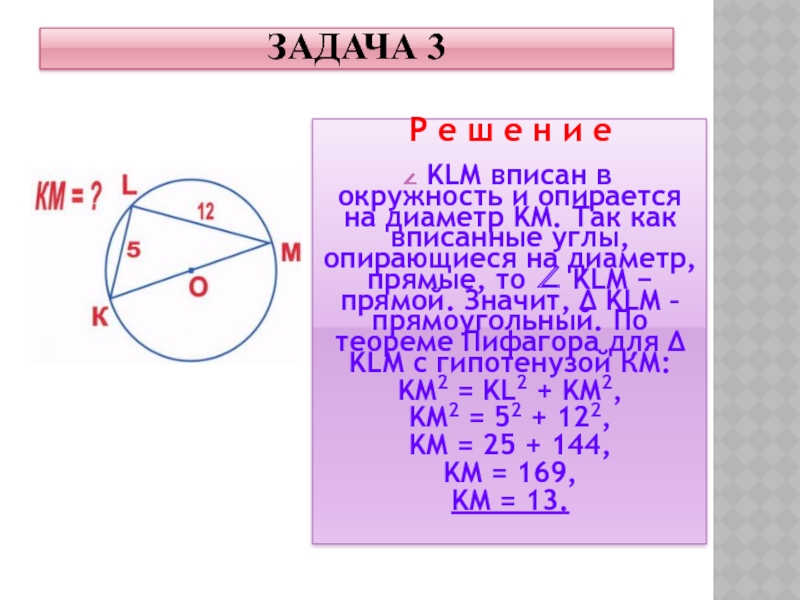
Р е ш е н и е
KLM вписан
в окружность и опирается на диаметр KM. Так как вписанные
углы, опирающиеся на диаметр, прямые, то ∠ KLM − прямой. Значит, Δ KLM – прямоугольный. По теореме Пифагора для Δ KLM с гипотенузой КМ:
KM2 = KL2 + KM2,
KM2 = 52 + 122,
KM = 25 + 144,
KM = 169,
KM = 13.
Слайд 18ПРАКТИЧЕСКАЯ ЗАДАЧА
Для крепления мачты нужно установить 4 троса. Один конец
каждого троса должен крепиться на высоте 12 м, другой на
земле на расстоянии 5 м от мачты.
Хватит ли 50 м троса для крепления мачты?
Анализируя математическую модель этой практической задачи, нужно найти гипотенузу прямоугольного треугольника по двум известным катетам.
Для решения этой проблемы можно организовать практическую работу исследовательского характера, предложив учащимся задание по рядам: построить прямоугольные треугольники с катетами 12 см и 5 см; 6 см и 8 см; 8 см и 15 см и измерить гипотенузу.
Результаты заносятся в таблицу.
а 12 6 8
b 5 8 15
с 13 10 17
Затем учащимся предлагается выразить формулой зависимость между длинами катетов и гипотенузой в прямоугольных треугольниках. Школьники выдвигают свои гипотезы, которые обсуждаются.
После установления зависимости между сторонами прямоугольного треугольника эмпирический вывод требует теоретического обоснования, т.е. доказывается теорема Пифагора.
Слайд 19ИСТОРИЧЕСКИЕ ЗАДАЧИ
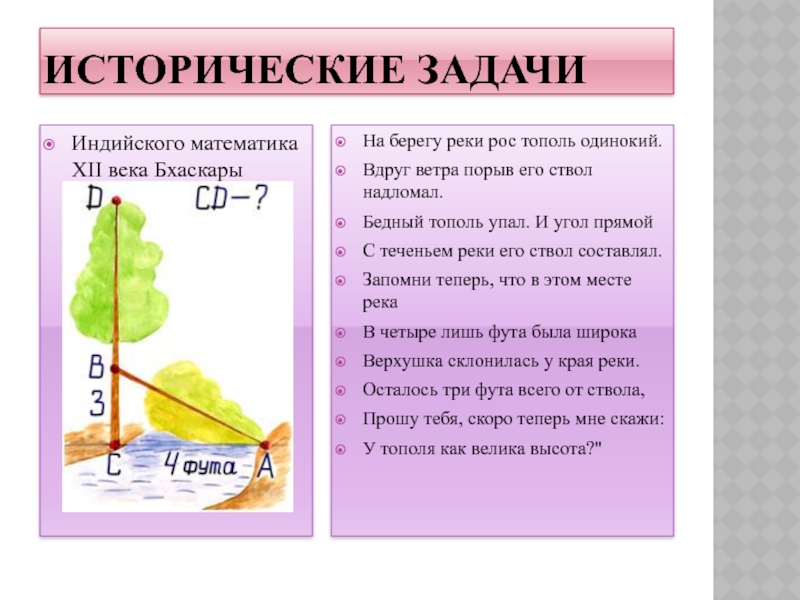
Индийского математика ХII века Бхаскары
На берегу реки рос тополь
одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол
прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?"
Слайд 20ЗАДАЧА ИЗ КИТАЙСКОЙ «МАТЕМАТИКИ В ДЕВЯТИ КНИГАХ»
"Имеется водоем со стороной
в 1 чжан = 10 чи. В центре его растет
камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его.
Спрашивается: какова глубина воды и какова длина камыша?"
Слайд 21ЗАДАЧА ИЗ УЧЕБНИКА АРИФМЕТИКИ ЛЕОНТИЯ МАГНИЦКОГО
"Случися некому человеку к стене
лестницу прибрати, стены же тоя высота есть 117 стоп. И
обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
Слайд 22ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА
Рассмотрим примеры практического применения теоремы Пифагора. Не
будем пытаться привести все примеры использования теоремы - это вряд
ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости.
Слайд 23КВАДРАТ И ПРЯМОУГОЛЬНИК
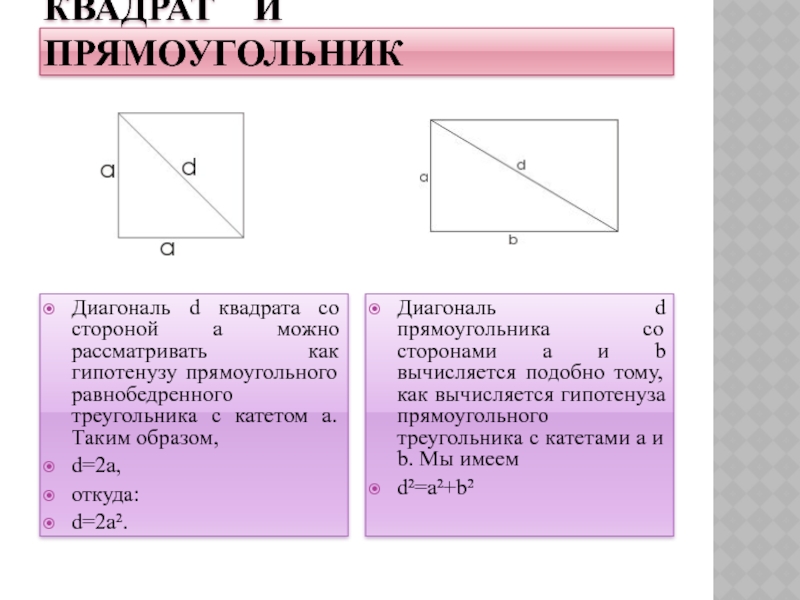
Диагональ d квадрата со стороной а
можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а.
Таким образом,
d=2a,
откуда:
d=2a².
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем
d²=a²+b²
Слайд 24ТРЕУГОЛЬНИК И КУБ
Высота h равностороннего треугольника
со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза
которого а, а другой катет a/2. Таким образом имеем
a=h+(a/2), или
h=(3/4)a.
Отсюда вытекает
???h=1/2 3a.
Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем
d=a+(2a), d=3a, d=3a.
Слайд 25ПИРАМИДА
Исследуем пирамиду, например, такую, в основании которой лежит квадрат и
высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть
сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды).
Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов - высота h, а другой - половина диагонали квадрата (1/2*2a). Вследствие этого имеем:
s=h+(1/2)a.
Затем можем вычислить высоту h1 боковых граней.
h1= h+(1/4)a.
Считать эти приложения теоремы Пифагора только теоретическими - большая ошибка. Если, например, рассматривать нашу четырехугольную пирамиду как крышу башни,
то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит:
"Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила ??? на перекрываемую площадь."

Слайд 26НЕКОТОРЫЕ ТЕОРЕМЫ И СЛЕДСТВИЯ , КОТОРЫЕ МОЖНО ВЫВЕСТИ ИЗ ТЕОРЕМЫ
ПИФАГОРА
Из теоремы Пифагора выявляются много разнообразных теорем и следствий из
них, которые изложены ниже.
Слайд 27ТЕОРЕМА 1
В прямоугольном треугольнике перпендикуляр, опущенный из вершины прямого угла
на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Слайд 28ТЕОРЕМА 2
В прямоугольном треугольнике каждый из катетов есть среднее пропорциональное
между гипотенузой и его проекцией на гипотенузу.
Слайд 29СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ПИФАГОРА
1. Квадрат стороны треугольника, лежащей против тупого
угла, больше суммы квадратов двух других его сторон.
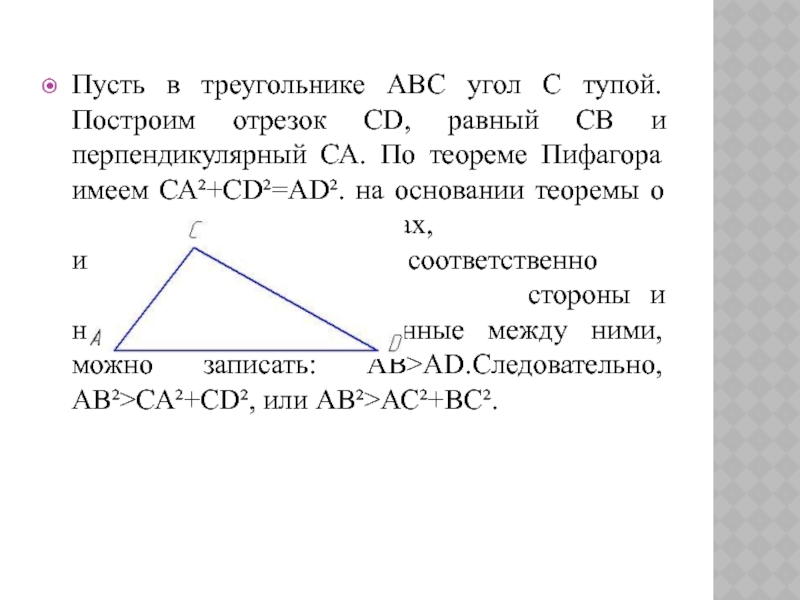
Слайд 30Пусть в треугольнике АВС угол С тупой. Построим отрезок СD,
равный СВ и перпендикулярный СА. По теореме Пифагора имеем СА²+СD²=AD².
на основании теоремы о треугольниках, имеющих соответственно по две равные стороны и неравные углы, заключенные между ними, можно записать: АВ>AD.Следовательно, АВ²>СА²+СD², или АВ²>АС²+ВС².
Слайд 312. Квадрат стороны треугольника, лежащей против острого угла, меньше суммы
квадратов двух других его сторон.
Слайд 32ТЕОРЕМА 3 (ОБРАТНАЯ ТЕОРЕМА ПИФАГОРА)
Если в треугольнике сумма квадратов двух
сторон равна квадрату третьей стороны , то треугольник прямоугольный и
третья сторона является его гипотенузой.
Слайд 33ТЕОРЕМА 4
Разность квадратов двух сторон треугольника равна разности квадратов их
проекций на третью сторону.
Слайд 34ТЕОРЕМА 5
Если на прямой даны две точки, то на этой
же прямой существует единственная точка, разность квадратов расстояний от которой
до данных двух точек равна квадрату длины данного.
Слайд 35ТЕОРЕМА 6
Если на стороне треугольника или на его продолжении дана
точка, разность квадратов расстояний от которой до вершин, определяющих эту
сторону, равна разности квадратов прилежащих сторон треугольника, то эта точка является основанием для высоты, опущенной на данную сторону треугольника.
Слайд 36ТЕОРЕМА 7
Если две прямые АВ и СD перпендикулярны, то имеет
место равенство
СА² - СВ²=DA² - DВ².
Слайд 37132=122+52
169=144+25
Задача.
Является ли треугольник прямоугольным, если его стороны 12см, 5см и
13 см.
132=122+52
169=144+25
Слайд 38ЗАКЛЮЧЕНИЕ
В заключении еще раз хочется сказать о важности теоремы. Значение
её прежде всего состоит в том, что из неё или
с её помощью можно вывести большинство теорем геометрии. К сожалению невозможно привести все доказательства теоремы, однако хочется надеяться, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера ,проявляемом по отношению к ней.