Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разбор заданий типа С1 ЕГЭ по математике
Содержание
- 1. Разбор заданий типа С1 ЕГЭ по математике
- 2. Презентация содержит разбор заданий типа С1 Единого
- 3. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение:
- 4. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 5. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 6. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуОтвет: а) б) №1
- 7. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение:
- 8. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 9. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 10. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуОтвет: а) б) №2
- 11. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение:
- 12. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение (продолжение): Вернёмся к замене:№3
- 13. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 14. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуОтвет: а) №3б)
- 15. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение:
- 16. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение (продолжение): №4
- 17. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 18. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуОтвет: №4а) б)
- 19. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение:
- 20. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение (продолжение): №5
- 21. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 22. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуОтвет: №5а) б)
- 23. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение:
- 24. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуРешение
- 25. а) Решите уравнениеб) Найти корни, принадлежащие отрезкуОтвет: а)№6б)
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Презентация содержит разбор заданий типа С1 Единого Государственного Экзамена по
математике 2014 года.
Приведенные задания могут иметь другие варианты решений!
Все задания,
представленные в презентации, взяты с сайта http://alexlarin.netСлайд 3а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение:
а) Используя формулы
приведения и синуса двойного аргумента, получим:
Вынесем общий множитель
за скобки: Произведение равно нулю, когда хотя бы один из множителей равен нулю, т.е. получаем совокупность уравнений:
№1
Слайд 4а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
Первое уравнение
совокупности представляет собой частный случай, корни которого:
Второе уравнение совокупности является
однородным. Разделив его обе части на , получим:№1
Слайд 5а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
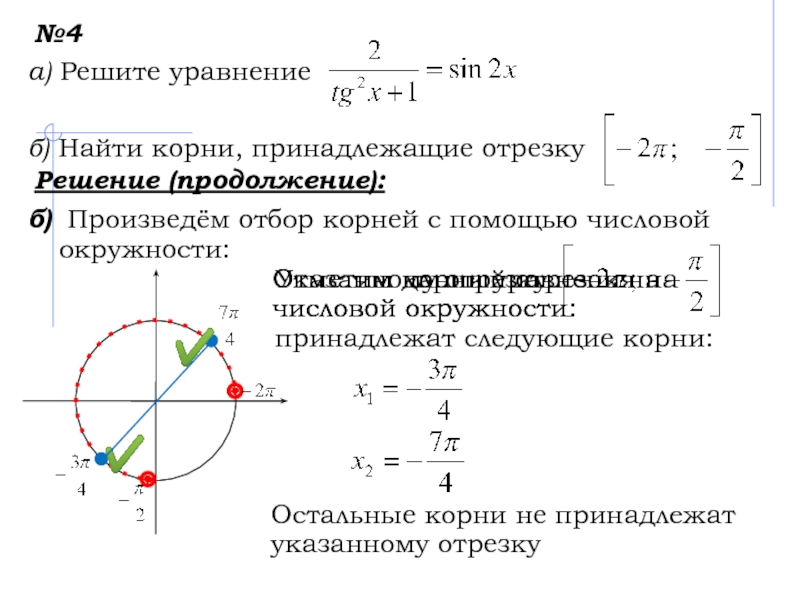
б) Произведём отбор
корней с помощью числовой окружности:
Отметим на числовой окружности данный отрезок.
Отметим
на числовой окружности первую серию корнейОтметим на числовой окружности вторую серию корней
Указанному отрезку
принадлежат следующие корни:
Остальные корни не принадлежат указанному отрезку
№1
Слайд 7а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение:
а) Используя формулы
приведения и косинуса двойного аргумента, получим:
Вынесем общий множитель
за скобки: Произведение равно нулю, когда хотя бы один из множителей равен нулю, т.е. получаем совокупность уравнений:
№2
Слайд 8а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
№2
Первое
уравнение совокупности представляет собой частный случай, корни которого:
Решение второго уравнения
совокупности:Слайд 9а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
№2
б) Произведём
отбор корней с помощью числовой окружности:
Отметим данный отрезок на числовой
окружности:Отметим первую серию корней на числовой окружности:
Отметим вторую серию корней на числовой окружности:
Указанному отрезку
принадлежат следующие корни:
Остальные корни не принадлежат указанному отрезку
Слайд 11а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение:
а) Используя основное
тригонометрическое тождество и формулы приведения, получим:
Произведём замену:
№3
, причём
– не удовлетворяет
условиюСлайд 12а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
Вернёмся к
замене:
№3
Слайд 13а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
б) Произведём
отбор корней с помощью двойного неравенства:
№3
Вычтем из обеих частей
неравенства
Разделим обе
части неравенствана
Т.к. , то полученному неравенству удовлетворяет
При
Слайд 15а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение:
а) ОДЗ уравнения:
Воспользуемся
формулой
№4
и формулой синуса двойного аргумента. Получим:
Произведение равно нулю, когда хотя
бы один из множителей равен нулю, но с учётом ОДЗ получаем однородное уравнение: Вынесем общий множитель за скобки:
Слайд 17а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
№4
б) Произведём отбор
корней с помощью числовой окружности:
Отметим данный отрезок на числовой окружности:
Отметим
корни уравнения на числовой окружности:Указанному отрезку
принадлежат следующие корни:
Остальные корни не принадлежат указанному отрезку
Слайд 19а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение:
а)
№5
В левой
части уравнения применим формулу приведения, а в правой – основное
тригонометрическое тождество. Получим:Вынесем общий множитель за скобки:
Произведение равно нулю, когда хотя бы один из множителей равен нулю, т.е. получаем совокупность уравнений:
Слайд 21а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
№5
б) Произведём отбор
корней с помощью числовой окружности:
Отметим данный отрезок на числовой окружности:
Отметим
на числовой окружности первую серию корней:Отметим на числовой окружности вторую серию корней:
Указанному отрезку
принадлежат следующие корни:
Остальные корни не принадлежат указанному отрезку
Слайд 23а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение:
а) Сгруппируем 1-е
слагаемое со 2-м, 3-е – с 4-м:
№6
Т.к.
, то (более того, ).Слайд 24а) Решите уравнение
б) Найти корни, принадлежащие отрезку
Решение (продолжение):
б) Произведём
отбор корней с помощью числовой окружности:
№6
Отметим данный отрезок на числовой
окружности:
Отметим на числовой окружности корни уравнения:
Указанному отрезку
принадлежат следующие корни:
Остальные корни не принадлежат указанному отрезку