Тела вращения

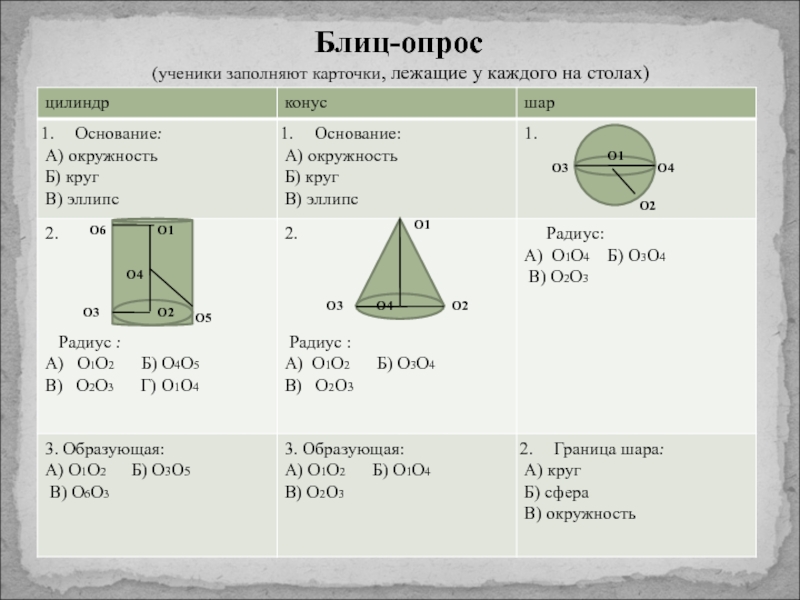
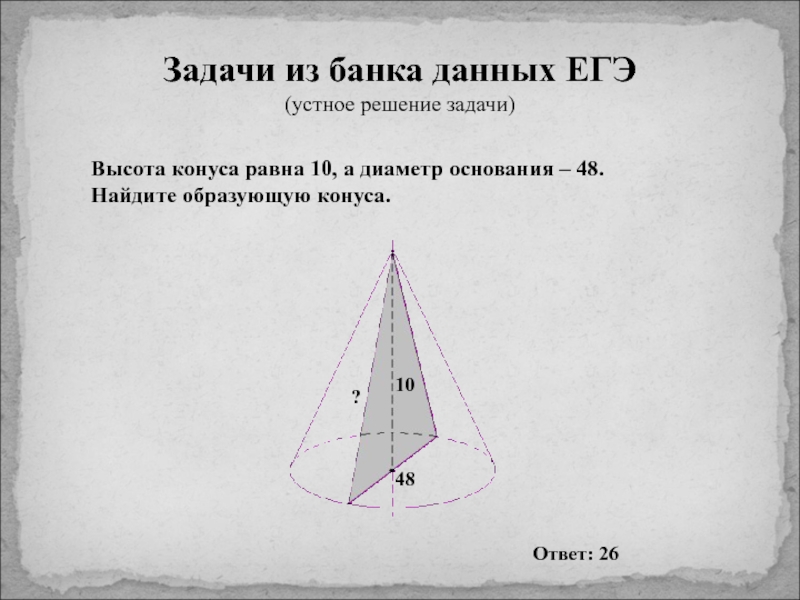
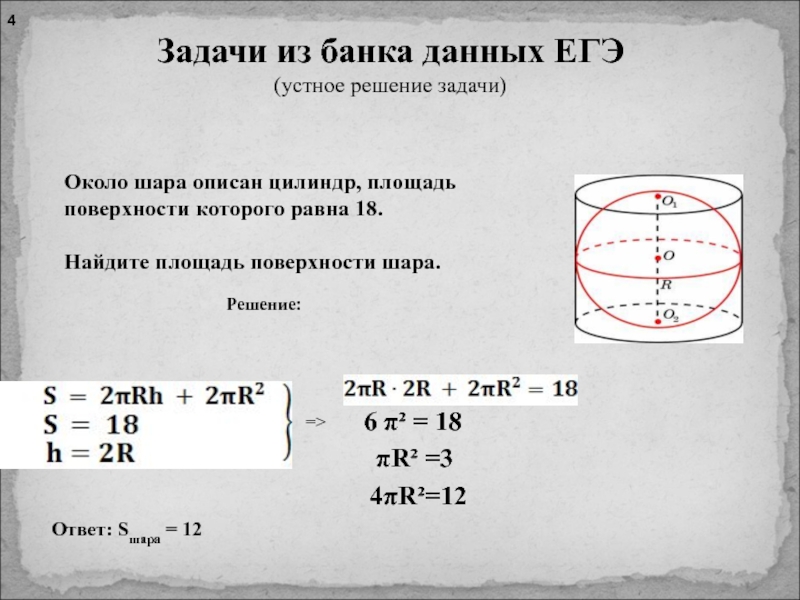
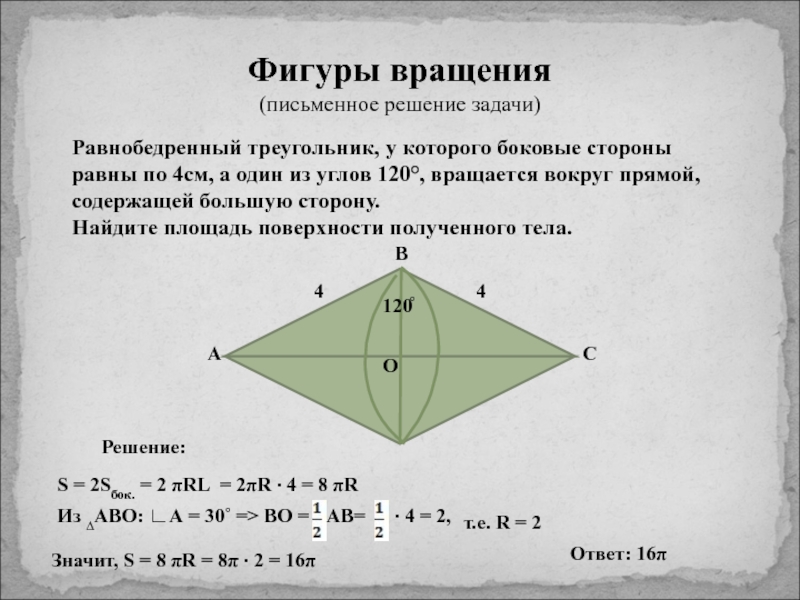
элементов фигур, площади поверхности.
Закрепление навыков решения задач уровня ЕГЭ.

Развитие самостоятельности при решении задач.
Развитие алгоритмического мышления.
Развитие пространственного воображения.
Воспитание контроля и самоконтроля.

правильно мыслить и рассуждать»
Г. Галилей

Шаром принято называть тело,
ограниченное сферой, т.е. шар и сфера –
это разные геометрические тела.

Однако оба слова «шар» и «сфера» происходят от одного и того же
греческого слова «сфайра» - мяч. При этом слово «шар» образовалось
от перехода согласных сф в ш.

В ХI книге «Начала» Евклид определяет шар как фигуру, описанную
вращающимся около неподвижного диаметра полукругом.

В древности сфера была в большом почёте. Астрономические
наблюдения над небесным сводом неизменно вызывали образ сферы.
Сфера всегда широко применялась в различных областях науки и техники.

слова 
Конус в переводе с греческого “konos” означает
«сосновая

шишка».
С конусом и цилиндром люди знакомы с глубокой древности.
Архимед решил задачу об объеме общей части
пересекающихся цилиндров.
Демокрит получил формулу для вычисления объема
пирамиды и конуса.
Школе Платона принадлежит:
а) исследование свойств цилиндра и конуса;
б) изучение конических сечений.
Большой трактат о конических сечениях был написан
Аполлонием Пергским – учеником Евклида

, что означает «валик», «каток».

Это форма рельефа,
образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными
горными

реками на предгорную равнину или в более плоскую широкую долину.

В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.

«Конусами» называется семейство морских
моллюсков. Раковина коническая (2–16 см),
ярко окрашенная.

По статистике на Земле ежегодно гибнет от разрядов
молний 6 человек на 1000 000 жителей .
Этого бы не случалось, если бы везде были громоотводы,
так как образуется конус безопасности. Чем выше
громоотвод, тем больше объем такого конуса.

а диаметр основания – 48.
Найдите образующую конуса.



10
48
?
Ответ: 26

диаметр основания конуса
6
10
Задачи из банка данных ЕГЭ (устное решение задачи)
?
Ответ: 16

8. Найдите высоту цилиндра.

8
S = 2πR h
S = 16π
→ 16π

= 8πh
h = 2

2R =8

Задачи из банка данных ЕГЭ (устное решение задачи)

Ответ: 2

Решение:

площадь сферы равна 16π


S = 4πR²
S = 16π
R

= 2

16π =

4πR²

→

Ответ: 2

Решение:

площадь боковой поверхности конуса, если его образующую увеличить в 3

раза?

S = πRL

S1 = πR(3L) = 3 (πRL) = 3 S

R

L

Ответ: в 3 раза

3L

R

Решение:

площадь
поверхности которого равна 18.

Найдите площадь поверхности шара.

Решение:

=>

Ответ: Sшара = 12

6 π² = 18

4

4πR²=12

πR² =3

единичной сферы.

Найдите его площадь поверхности.
Решение:
Т.к. сфера вписана в параллелепипед,

то ABCDA1B1C1D1 является кубом, в котором а = 2R = 2 ∙ 1 = 2
Значит, S = 6a² = 6 ∙ 2²= 24

Ответ: 24

4см, а один из углов 120°, вращается вокруг прямой,
содержащей большую

сторону.
Найдите площадь поверхности полученного тела.

4

4

120̊

Решение:

A

B

C

O

т.е. R = 2

Значит, S = 8 πR = 8π ∙ 2 = 16π

Ответ: 16π

S = 2Sбок. = 2 πRL

= 2πR ∙ 4 = 8 πR

Из ∆АВО: ∟А = 30˚ => ВО =

АВ=

∙ 4 = 2,

вращается
вокруг большей стороны. Найдите площадь поверхности тела вращения.






A
D
B
C
Решение:

S = Sбок. + 2Sосн.
S = 2πRh + 2πR2
Из прямоугольника ABCD : S = AB ∙ BC = 15
P = 2 (AB +BC) = 16
Или, Rh = 15
R + h = 8,



Ответ: 48π см2

значит, R = 3, h = 5

Таким образом,

S = 2π ∙15 + 2π ∙ 32 =

48π (см2)

2 вариант – 24π; 5√2

данным условиям задач и решите их:

Дан шар,

радиус которого 2см.
Длина окружности основания цилиндра 8π см, а диагональ
осевого сечения 17см.
Прямоугольная трапеция с основаниями 2 и 5 см и меньшей боковой стороной 4 см вращается вокруг большего основания.

2. Рефлексия (бланки опроса лежат на столах учащихся).
Поставьте «плюс» или «минус» напротив каждого утверждения

Я знаю формулы для нахождения площадей поверхностей тел вращения.
Я понял, как решать типовые задачи уровня ЕГЭ.
Я расширил свои знания о телах вращения.