Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Прямоугольная система координат в пространстве. Векторы. Действия над векторами."
Содержание
- 1. Презентация по теме "Прямоугольная система координат в пространстве. Векторы. Действия над векторами."
- 2. Если через точку пространства проведены три попарно
- 3. Прямые с выбранными на них направлениями называются
- 4. Три плоскости, проходящие через оси координат Ох
- 5. Точка О разделяет каждую из осей координат
- 6. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами.
- 7. Точка лежитна осиОу (0; у; 0)Ох (х;
- 8. Слайд 8
- 9. Слайд 9
- 10. Начертить прямоугольную трехмерную систему координат и отметить
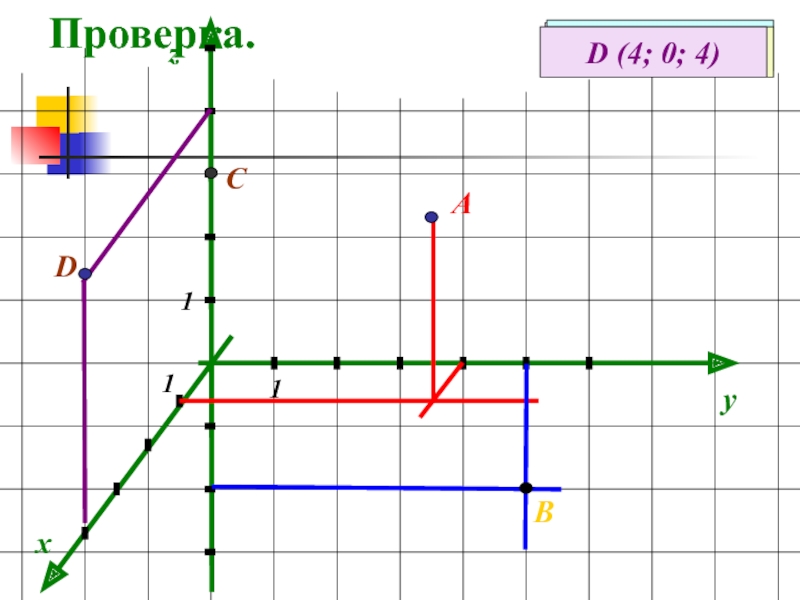
- 11. Проверка.xyzА (1; 4; 3)АВ (0; 5; -2)111ВС (0; 0; 3)СD (4; 0; 4)D
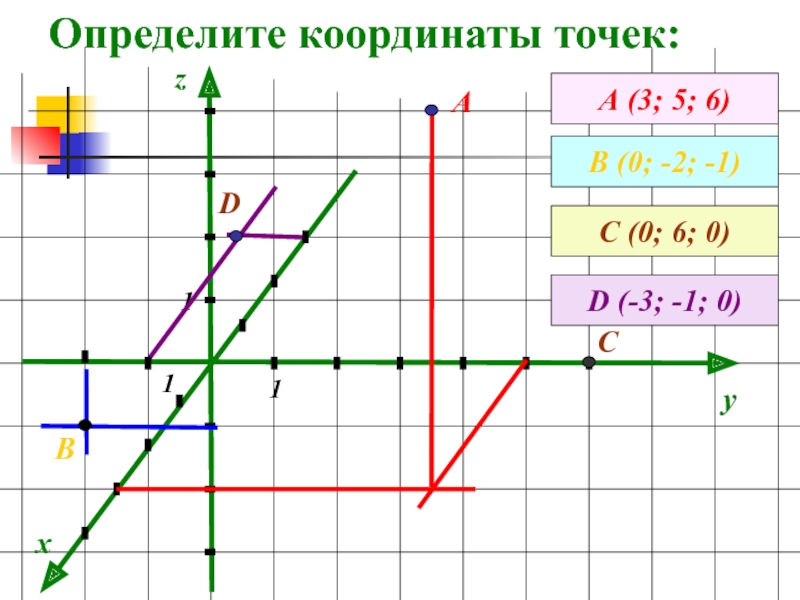
- 12. Определите координаты точек:xyzА (3; 5; 6)АВ (0; -2; -1)111ВС (0; 6; 0)СD (-3; -1; 0)D
- 13. Векторы. Действия над векторами.
- 14. АВВектором называется направленный отрезок, имеющий определеннуюдлину.
- 15. Координаты вектораВекторы (i. j. k) единичные векторыЛюбой вектор можно разложить по координатным векторамНазад
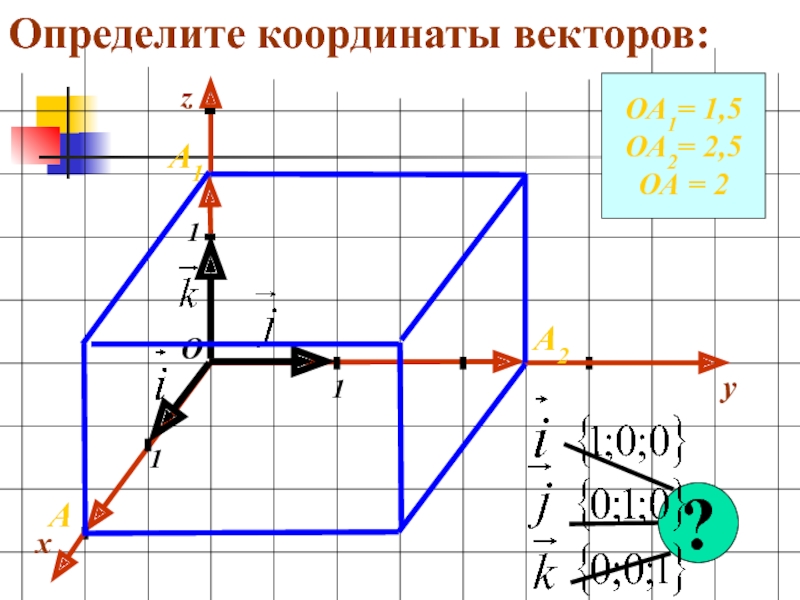
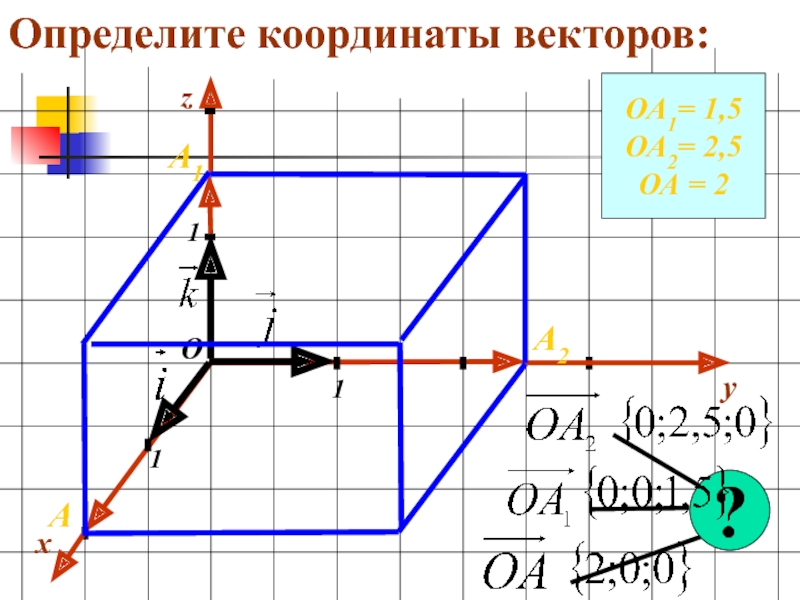
- 16. Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?
- 17. Определите координаты векторов:xy111ОzОА1= 1,5ОА2= 2,5ОА = 2А1А2А?
- 18. Коэффициенты х, у и z в разложении
- 19. Правила действий над векторами с заданными координатами.1.
- 20. Правила действий над векторами с заданными координатами.2.
- 21. Правила действий над векторами с заданными координатами.3.
- 22. Правила действий над векторами с заданными координатами.4.
- 23. Абсолютная величинаНазад
- 24. Скачать презентанцию
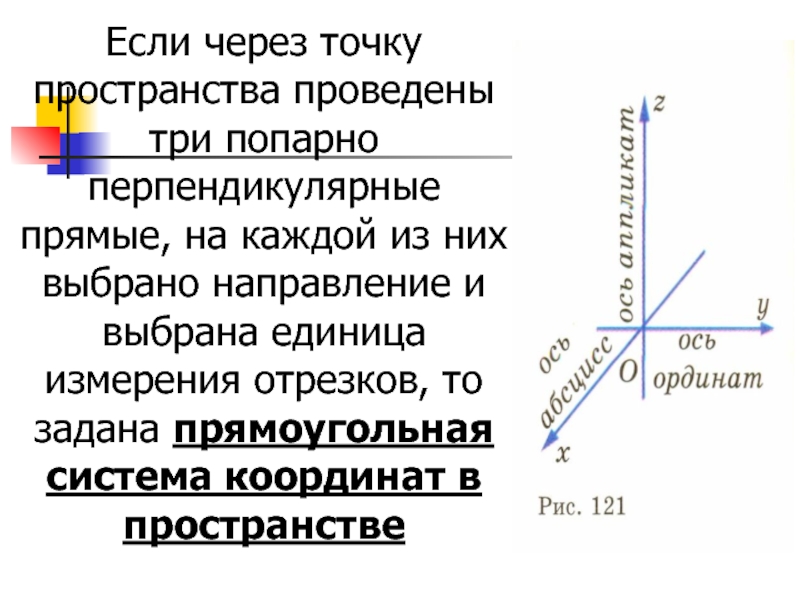
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то задана прямоугольная система координат в пространстве
Слайды и текст этой презентации
Слайд 2Если через точку пространства проведены три попарно перпендикулярные прямые, на
каждой из них выбрано направление и выбрана единица измерения отрезков,
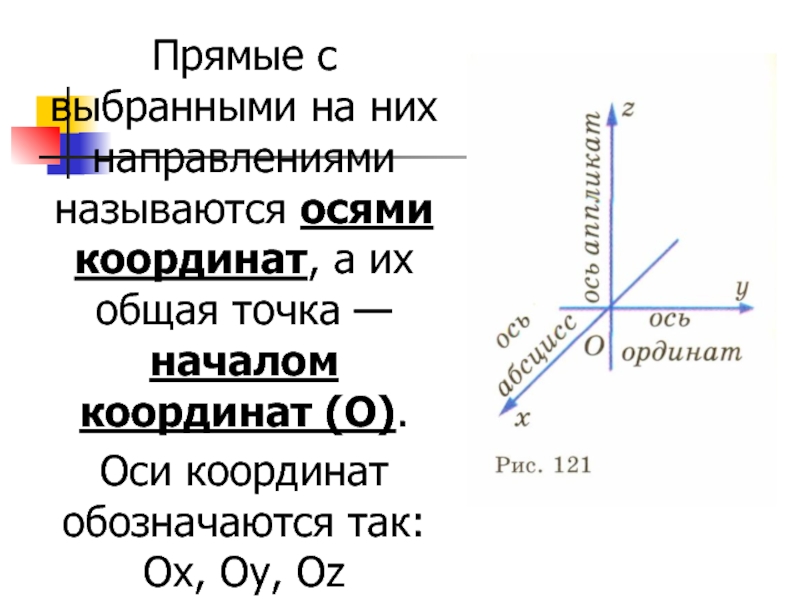
то задана прямоугольная система координат в пространстве
Слайд 3Прямые с выбранными на них направлениями называются осями координат, а
их общая точка — началом координат (О).
Оси координат обозначаются
так: Ох, Оу, Оz
Слайд 4Три плоскости, проходящие через оси координат Ох и Оу, Оу
и Оz, Оz и Ох, называются координатными плоскостями: Оху, Оуz,
Оzх.
Слайд 5Точка О разделяет каждую из осей координат на два луча.
Луч, направление которого совпадает с направлением оси, называется положительной полуосью,
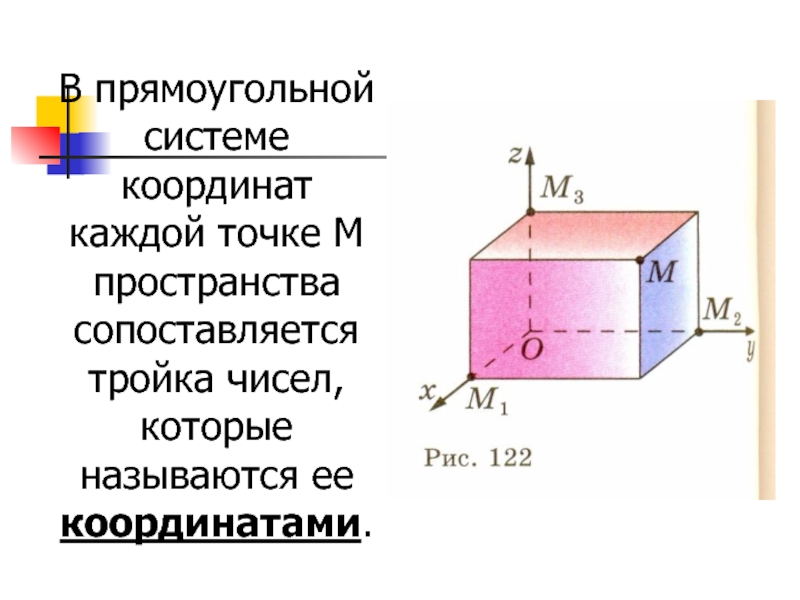
а другой луч отрицательной полуосью.
Слайд 6В прямоугольной системе координат каждой точке М пространства сопоставляется тройка
чисел, которые называются ее координатами.
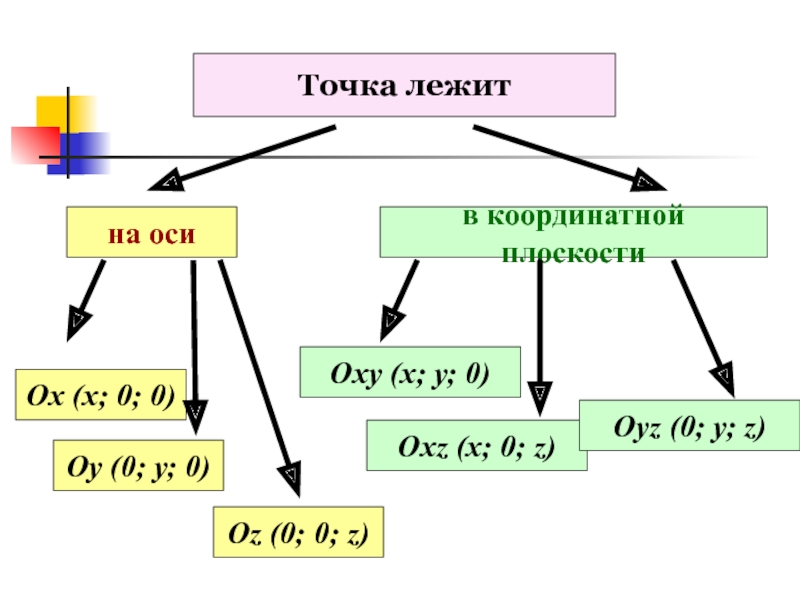
Слайд 7Точка лежит
на оси
Оу (0; у; 0)
Ох (х; 0; 0)
Оz (0;
0; z)
в координатной плоскости
Оху (х; у; 0)
Охz (х; 0; z)
Оуz
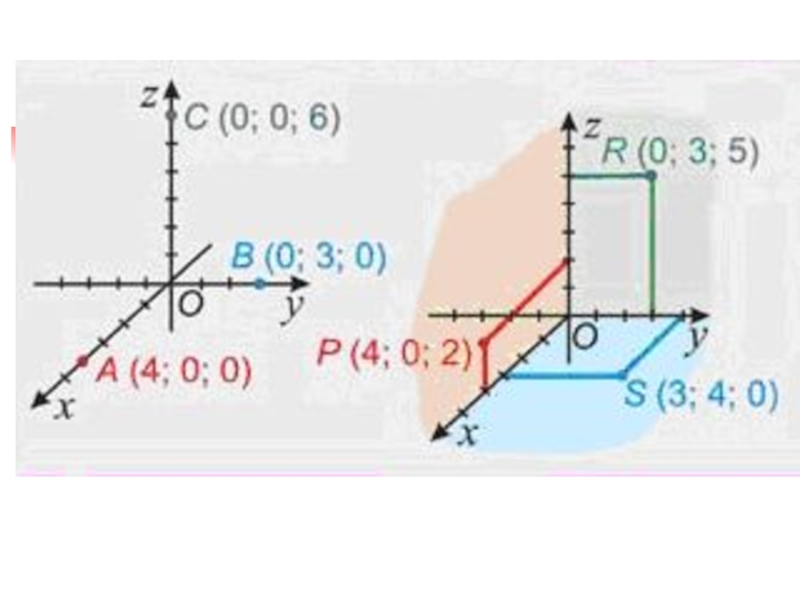
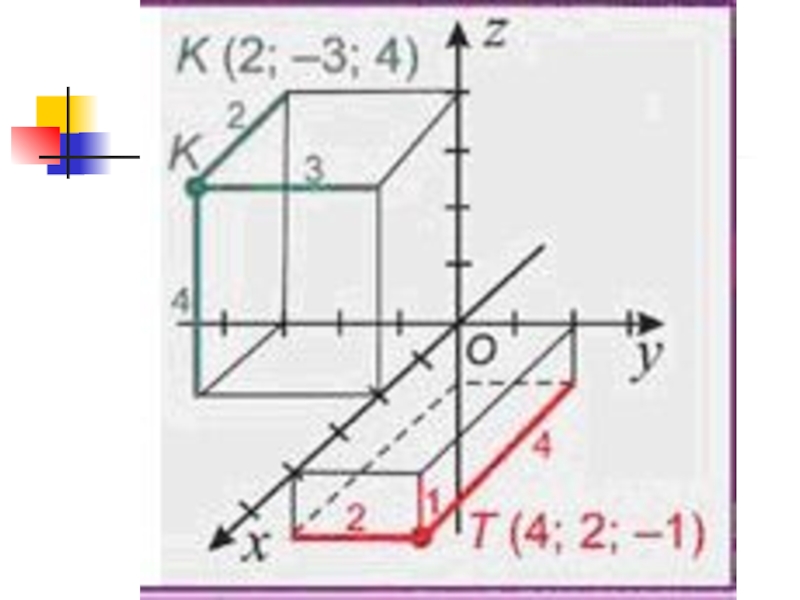
(0; у; z)
Слайд 10Начертить прямоугольную трехмерную систему координат и отметить в ней точки:
А (1; 4; 3); В (0; 5; -2);
С (0;
0; 3) и D (4; 0; 4)
Слайд 15Координаты вектора
Векторы (i. j. k) единичные векторы
Любой вектор можно разложить
по координатным векторам
Назад
Слайд 18Коэффициенты х, у и z в разложении вектора a по
координатным векторам называются координатами вектора a в данной системе координат.
Слайд 19Правила действий над векторами с заданными координатами.
1. Равные векторы имеют
равные координаты.
Пусть
х1 = х2; у1 = у2; z1 = z2
Слайд 20Правила действий над векторами с заданными координатами.
2. Каждая координата суммы
двух (и более) векторов равна сумме соответствующих координат этих векторов.
Слайд 21Правила действий над векторами с заданными координатами.
3. Каждая координата произведения
вектора на число равна произведению соответствующей координаты на это число.
α
– произв.число
Слайд 22Правила действий над векторами с заданными координатами.
4. Каждая координата разности
двух векторов равна числу разности соответствующих координат на этих векторов.
