Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по теме "Прямоугольная система координат в пространстве"
Содержание
- 1. Презентация по теме "Прямоугольная система координат в пространстве"
- 2. Задание прямоугольной системы координат в пространствеОyОy
- 3. Нахождение координат точек (Работа с учебником по
- 4. Даны точки:А (2; -1; 0)В (0; 0;
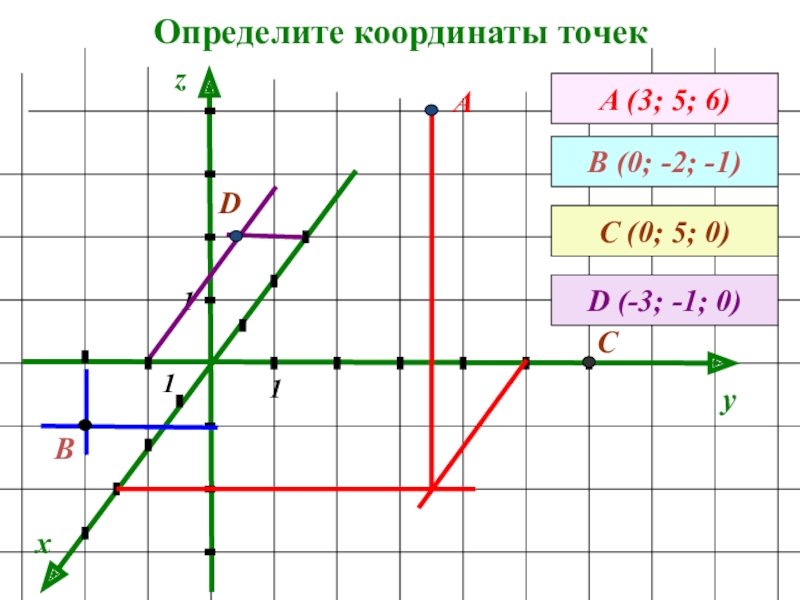
- 5. Определите координаты точекxyzА (3; 5; 6)АВ (0; -2; -1)111ВС (0; 5; 0)СD (-3; -1; 0)D
- 6. Координаты вектора x
- 7. Координаты вектораxy111Оz
- 8. Правила действий над векторами с заданными координатами1.
- 9. 2. Каждая координата суммы двух (и более) векторов равна сумме соответствующих координат этих векторовДано:Следовательно
- 10. 3. Каждая координата произведения вектора на
- 11. Выполнить задание устно:Даны векторы:Найти вектор равный:
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Прямоугольная система координат в пространстве
Геометрия – 11 класс
Белоброва Татьяна Валерьевна
учитель
математики высшей категории
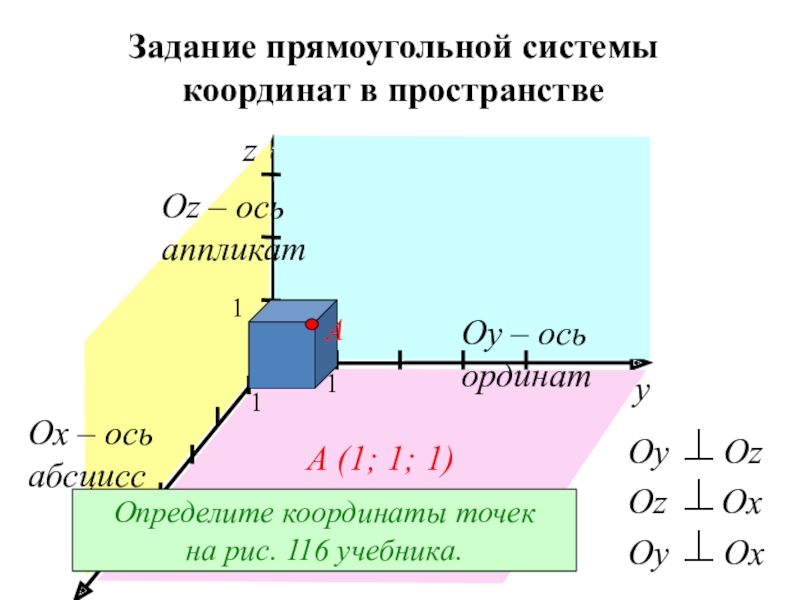
Слайд 2Задание прямоугольной системы
координат в пространстве
О
y
Оy Оz
Оz
Оx
Оy Оx
x
z
1
1
1
A
A (1; 1; 1)
Ох – ось
абсциссОу – ось ординат
Оz – ось аппликат
Определите координаты точек
на рис. 116 учебника.
Слайд 3Нахождение координат точек
(Работа с учебником по рис 116)
Точка лежит
на оси
Оу
(0; у; 0)
Ох (х; 0; 0)
Оz (0; 0; z)
в координатной
плоскостиОху (х; у; 0)
Охz (х; 0; z)
Оуz (0; у; z)
№ 400 – устно.
Слайд 4 Даны точки:
А (2; -1; 0)
В (0; 0; -7)
С (2; 0;
0)
D (-4; -1; 0)
Е (0; -3; 0)
F (1; 2; 3)
Р
(0; 5; -7)К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz
Назовите точки, лежащие
в плоскости Охz
Назовите точки, лежащие
в плоскости Оху
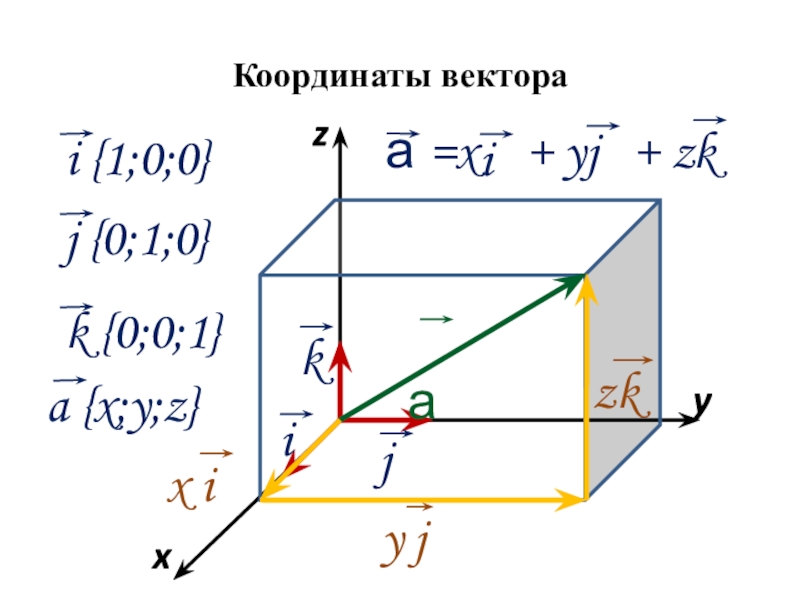
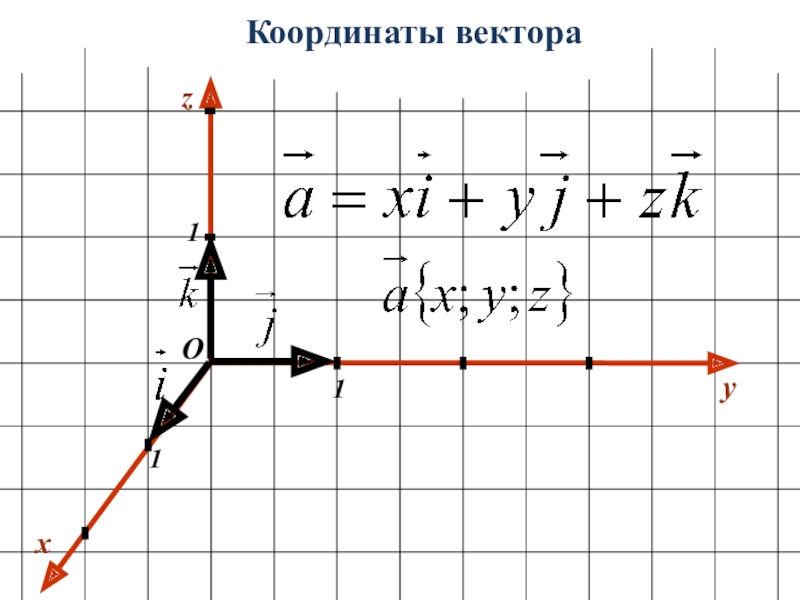
Слайд 6Координаты вектора
x
y
z
а
i
k j
а =x + y + z
i
j
k
x i
y j
zk
i {1;0;0}
j {0;1;0}
k {0;0;1}
a {x;y;z}
Слайд 8Правила действий над векторами с заданными координатами
1. Равные векторы имеют
равные координаты
Пусть
, тогда
х1 = х2; у1 = у2; z1 =
z2 Слайд 9
2. Каждая координата суммы двух (и более) векторов равна
сумме соответствующих координат этих векторов
Дано:
Следовательно
Слайд 10
3. Каждая координата произведения вектора на число равна произведению
соответствующей координаты на это число.
4. Каждая координата разности двух векторов
равна разности соответствующих координат на этих векторов.Дано: