Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в логику
Содержание
- 1. Введение в логику
- 2. Дж. Буль (1815 – 1864) – анг.
- 3. Клод Шеннон – отец современных теорий информации
- 4. Логическое высказывание - это любое повествовательное пpедлoжение,
- 5. Какие из предложений являются высказыванием? Определите их
- 6. Логические операции
- 7. Умозаключение – это форма мышления, с помощью
- 8. ЗаданияЗаписать в виде логического выражения: «Летом Петя
- 9. Задания 3. Запишите следующие высказывания в виде логических
- 10. Конъюнкция (операция «и»)Истинно, тогда и только тогда, когда оба высказывания истинны.
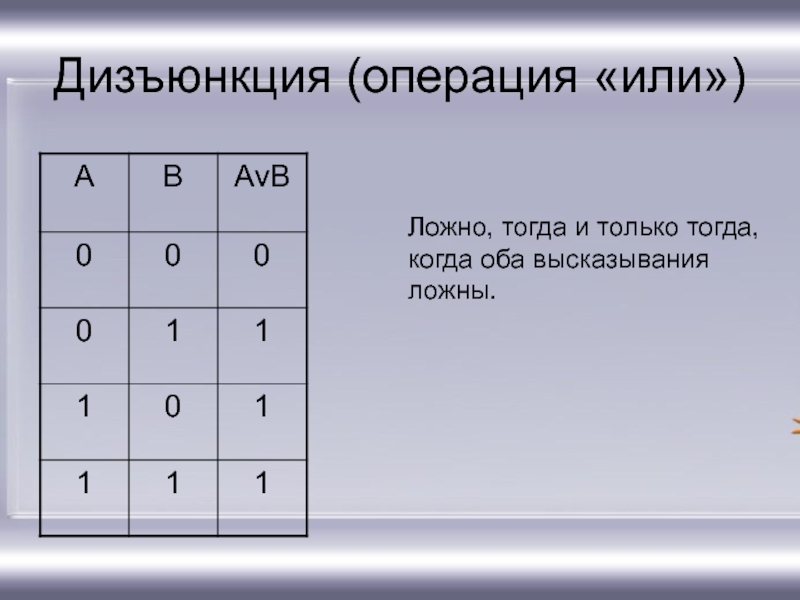
- 11. Дизъюнкция (операция «или»)Ложно, тогда и только тогда, когда оба высказывания ложны.
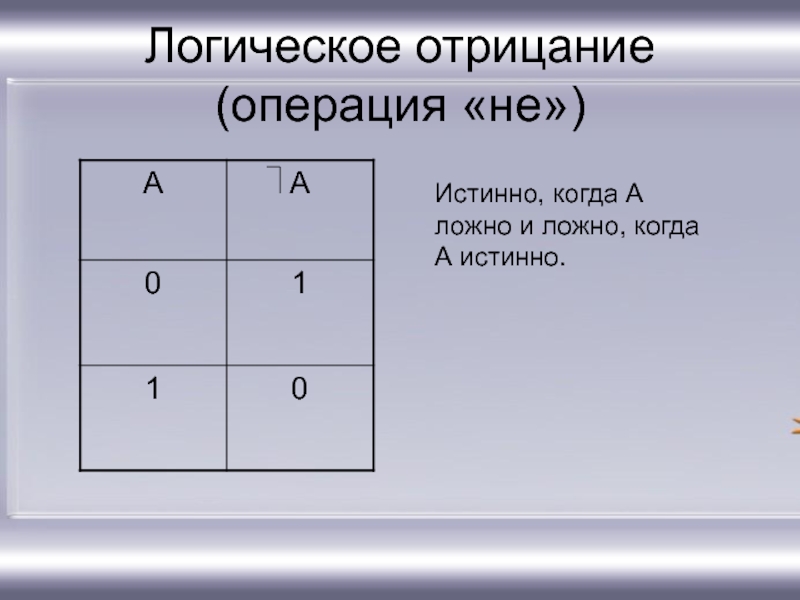
- 12. Логическое отрицание (операция «не»)Истинно, когда А ложно и ложно, когда А истинно.
- 13. ЗаданияНайдите значения логических выражений:F = (0v0)v(1v1)F = (1v1)v(1v0) F = ((1v0)v1)v1)F = (0^1)^1
- 14. Задания
- 15. Домашнее заданиеИз двух простых высказываний постройте сложное
- 16. 2. Составьте и запишите истинные сложные высказывания
- 17. 3. Даны два простых высказывания A={2*2=4}, B
- 18. Скачать презентанцию
Дж. Буль (1815 – 1864) – анг. математик отец алгебры логикиБулева алгебра (алгебра логики) изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например, {0,1}).
Слайды и текст этой презентации
Слайд 2Дж. Буль (1815 – 1864) – анг. математик отец алгебры
логики
аргументы, и значения принадлежат заданному двухэлементному множеству (например, {0,1}).Слайд 3Клод Шеннон – отец современных теорий информации и связи
В
1938 году защитил докторскую диссертацию, в которой разработал принципы логического
устройства компьютера, соединив булеву алгебру с функционированием релейно-контактных и электронно-ламповых схем.Клод Шеннон (1916-2001) – американский математик и инженер
Слайд 4Логическое высказывание - это любое повествовательное пpедлoжение, в oтнoшении кoтopoгo
можно oднoзначнo сказать, истинно оно или лoжнo.
Примеры:
"3 — простое
число"- высказывание, так как оно истинное.
"Париж — столица Японии" - высказывание, так как оно ложное. Высказываниями не являются, например, предложения "ученик десятого класса" и "информатика — интересный предмет". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие “интересный предмет”. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа "в городе A более миллиона жителей", "у него голубые глаза" не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь.
Слайд 5Какие из предложений являются высказыванием? Определите их истинность.
Какой длины эта
лента?
Прослушайте сообщение.
Число 11 является простым.
Делайте утреннюю зарядку!
Назовите устройство ввода информации.
Кто
отсутствует?Все медведи – бурые.
Слайд 7Умозаключение – это форма мышления, с помощью которой из одного
или нескольких суждений может быть получено новое суждение (умозаключение)
Логическая переменная
– это простое высказывание, содержащее только одну мысль (обозначение А, В, С и т.д.).Значением логического выражения могут быть только ЛОЖЬ (0) или ИСТИНА (1).
Слайд 8Задания
Записать в виде логического выражения: «Летом Петя поедет в деревню
и, если будет хорошая погода, то он пойдет на рыбалку».
Есть
два простых высказывания: А – «Число 10 – четное»;
В – «Волк травоядное животное».
Составьте из них все возможные составные высказывания и определите их истинность.
Слайд 9Задания
3. Запишите следующие высказывания в виде логических выражений:
А) Число 17
нечетное и двузначное.
Б) Неверно, что корова – хищное животное.
С) Если
компьютер включен, то можно на нем работать.Слайд 13Задания
Найдите значения логических выражений:
F = (0v0)v(1v1)
F = (1v1)v(1v0)
F = ((1v0)v1)v1)
F
= (0^1)^1
Слайд 15Домашнее задание
Из двух простых высказываний постройте сложное высказывание, используя «и»,
«или». Запишите логические высказывания с помощью логических операций и определите
их истинность:а) На полке стоят учебники. На полке стоят справочники.
б) Часть детей – девочки. Остальные – мальчики.
Слайд 162. Составьте и запишите истинные сложные высказывания из простых с
использованием логических операций.
а) Любое из чисел X, Y, Z положительно.
б)
Любое из чисел X, Y, Z отрицательно.в) Хотя бы одно из чисел X, Y, Z не отрицательно.
г) Все числа X, Y, Z равны 12.
д) Если X делится на 9, то X делится и на 3.
е) Если X делится на 2, то оно четное.
Слайд 173. Даны два простых высказывания
A={2*2=4}, B = {2*2=5}.
Какие из
составных высказываний истинны:
A^B; AvB; А; В.
4.Найдите значения логических выражений:
F =1^(1^1)^1
F = ((1v0)^(1^1))^(0v1)
F = ((1^0)v(1^0))v1
F = ((1^1)v0)^(0v1)
F = ((0^0)v0)^(1v1)