Слайд 1Комбинаторные задачи
в геометрии
Слайд 2В последнее время интерес к комбинаторике в школьном курсе математики
заметно возрос. Элементы комбинаторики, статистики и теории вероятностей включены в
новые стандарты по математике для основной и профильной школ. Формирование комбинаторных представлений и развитие комбинаторного мышления школьников входит в число основных целей обучения математике.
Обычно, когда говорят об элементах комбинаторики, имеют в виду задачи алгебраического содержания. Однако и комбинаторными задачами можно заниматься и на уроках геометрии, начиная с 7 по 11 класс.
Слайд 3Точки и прямые
на плоскости
Одной из первых аксиом геометрии, относящейся
к взаимному расположению точек и прямых на плоскости, является аксиома
о том, что через любые две точки плоскости проходит единственная прямая. Учащимся можно предложить следующие задачи, идущие с нарастанием сложности.
Слайд 4Точки и прямые
на плоскости
Сколько прямых проходит через различные пары
из трех точек, не лежащих на одной прямой?
Ответ:
3.
Сколько прямых проходит через различные пары из четырех точек, никакие три из которых не лежат на одной прямой?
Ответ: 6.
Сколько прямых проходит через различные пары из пяти точек, никакие три из которых не лежат на одной прямой?
Ответ: 10.
Слайд 5Точки и прямые
на плоскости
Сколько прямых проходит через различные пары
из n точек, никакие три из которых не лежат на
одной прямой? Укажите способ построения таких точек.
Решение. Пусть А1 …, Аn — n точек, никакие три из которых не лежат на одной прямой. Для построения таких точек достаточно отметить их на окружности.
Выясним, сколько прямых проходит через точку А1 и оставшиеся точки. Так как число оставшихся точек равно n – 1 и через каждую из них и точку А1 проходит одна прямая, то искомое число прямых будет равно n - 1. Заметим, что рассуждения, проведенные для точки А1, справедливы для любой точки. Поскольку всего точек n и через каждую из них проходит n - 1 прямая, то число посчитанных прямых будет равно n (n -1).
При указанном подсчете мы каждую прямую посчитали дважды и поэтому число прямых, проходящих через различные пары из n данных точек, равно n (n -1).
2
Слайд 6Точки и прямые
на плоскости
Какое наибольшее число точек попарных пересечений
могут иметь три прямые?
Ответ: 3.
Какое
наибольшее число точек попарных пересечений могут иметь четыре прямые?
Ответ: 6.
Какое наибольшее число точек попарных пересечений могут иметь пять прямых?
Ответ: 10.
Слайд 7Окружности
Вместо прямых на плоскости можно рассмотреть окружности и выяснить количество
их точек пересечения.
Какое наибольшее число точек пересечения могут иметь две
окружности?
Учащиеся изображают в тетради две окружности и выясняют, что наибольшее число точек пересечения
равно 2.
Какое наибольшее число точек попарных пересечений могут иметь три окружности?
Ответ: 6.
Слайд 8Многоугольники
Сколько диагоналей имеет четырехугольник?
Решение. Непосредственной проверкой убеждаемся, что
число диагоналей равно 2.
Сколько диагоналей имеет пятиугольник?
Ответ: число диагоналей равно
5.
Сколько диагоналей имеет шестиугольник?
Ответ: число диагоналей равно 9.
Слайд 9Многоугольники
Сколько диагоналей имеет n-угольник?
Решение. Зафиксируем какую-нибудь вершину
n-угольника. Учитывая, что диагональю является отрезок, соединяющий несоседние вершины многоугольника,
получаем, что через данную вершину проходит n - 3 диагонали. Поскольку общее число вершин равно n, через каждую из них проходит n - 3 диагонали, и при таком подсчете каждая диагональ считается дважды, получаем, что общее число диагоналей равно n(n-3)
2 .
Может ли многоугольник иметь:
а) 10 диагоналей;
б) 20 диагоналей;
в) 30 диагоналей.
Решение. По результатам предыдущей задачи шестиугольник имеет 9 диагоналей, семиугольник — 14, восьмиугольник — 20, девятиугольник — 27, десятиугольник — 35. Ясно, что многоугольники с большим числом сторон имеют большее число диагоналей. Поэтому многоугольник может иметь 20 диагоналей и не может иметь 40 или 30 диагоналей.
Слайд 10Многоугольники
Может ли прямая пересекать все стороны 2n-угольника?
Решение. Пример
приведен на рисунке.
Ответ: да.
Слайд 11Многоугольники
Какое наибольшее число точек самопересечения может иметь замкнутая
ломаная с пятью сторонами?
Решение. Каждая сторона ломаной может
пересекаться только с несоседними сторонами. Таких сторон у пятисторонней ломаной две. Значит, число точек самопересечения не превосходит 5x2 = 5.
2
Пример замкнутой пятисторонней
ломаной с пятью точками
самопересечения дает пентаграмма.
Слайд 12Многоугольники
Какое наибольшее число точек самопересечения может иметь замкнутая ломаная с
(2n + 1)-й стороной? Приведите примеры для n = 3,
n = 4.
Решение аналогично решению предыдущей задачи; примеры ломаных приведены на рисунке.
Ответ: (2n + 1)(n - 1).
Слайд 13Задачи на разрезание
Греческий крест (рис. 1) разрежьте на несколько частей
и составьте из них квадрат.
Решение. Заметим, что
если стороны квадратов, из которых составлен греческий крест, равны 1, то сторона искомого квадрата равна 5 . Требуемое разрезание показано на рисунке 2.
Рис. 1
Рис. 2
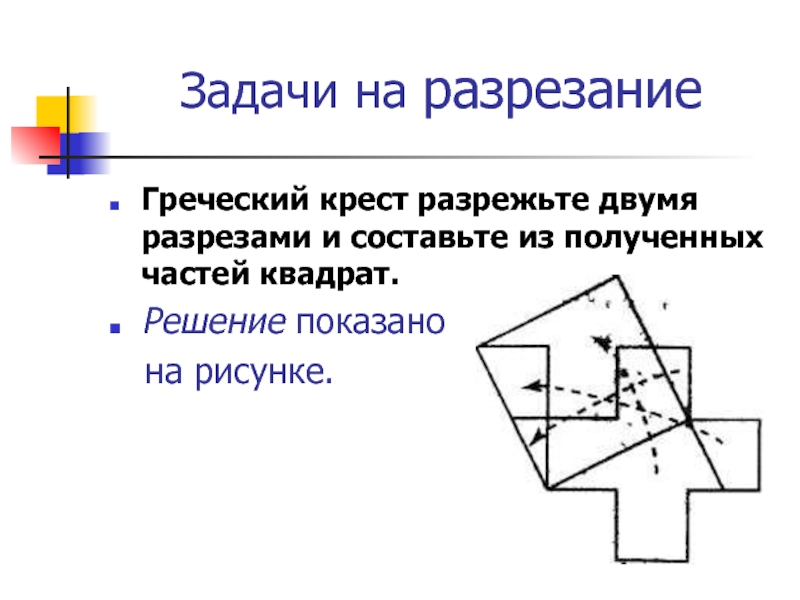
Слайд 14Задачи на разрезание
Греческий крест разрежьте двумя разрезами и составьте из
полученных частей квадрат.
Решение показано
на рисунке.
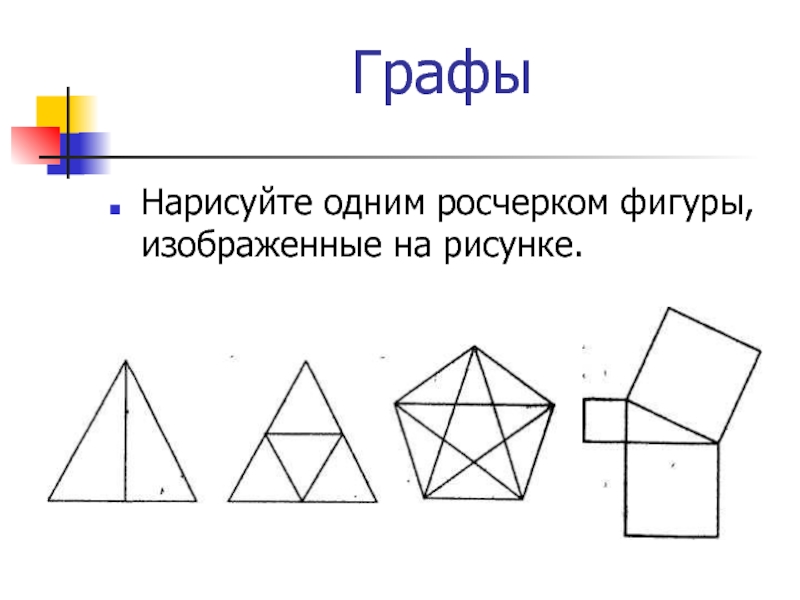
Слайд 15Графы
Нарисуйте одним росчерком фигуры, изображенные на рисунке.
Слайд 16Графы
Сможет ли экскурсовод провести посетителей по выставке, план которой
приведен на рисунке, так, чтобы они побывали в каждом зале
только один раз?
Вершины графа — это вход, выход, двери, соединяющие залы, перекрестки, а ребра — залы и коридоры. Где на выставке следовало бы сделать вход и выход, чтобы можно было провести, экскурсию по всем залам, побывав в каждом из них в точности один раз?
Слайд 17Теорема Эйлера
для многоугольников
Два соседа имеют:
а) три общих колодца;
б) четыре общих колодца.
Можно ли провести непересекающиеся
дорожки от каждого дома
к каждому
колодцу?
Слайд 18Прямые и плоскости
в пространстве
В пространстве даны n точек, никакие
четыре из которых не лежат в одной плоскости. Сколько плоскостей
проходит через различные тройки из этих точек?
Решение. Поскольку плоскость однозначно задается тремя точками, не лежащими на одной прямой, то число плоскостей равно числу сочетаний из n по три, то есть равно
n(n - 1)(n – 2)
6 .
Слайд 19Многогранники
Может ли в пирамиде быть 21 ребро?
Ответ:
нет, в пирамиде число ребер четно.
Может ли в призме быть
16 ребер?
Ответ: нет, в призме число ребер делится на три.
Чему равна число диагоналей в n-угольной призме?
Ответ: n (n - 3).
Сколько осей симметрии имеет куб?
Слайд 20Многогранники
Сколько имеется различных движений, переводящих в себя:
а) правильный
тетраэдр; б) куб;
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
Ответ: а) 24; б) 48; в) 48; г) 120; д) 120.
Может ли у многогранника быть семь ребер?
Решение. В вершинах такого многогранника не может сходиться четыре ребра, так как в этом случае число ребер многогранника было бы больше семи. Если же в каждой вершине многогранника сходится по три ребра, то число ребер многогранника должно делиться на три.
Ответ: нет.
Слайд 21Теорема Эйлера
для многогранников
Решение большого класса комбинаторных задач по геометрии
основывается на теореме Эйлера о числе вершин, ребер и граней
выпуклого многогранника.
Гранями выпуклого многогранника являются только треугольники. Сколько у него вершин и граней, если он имеет:
а) 12 ребер; б) 15 ребер?
Ответ: а) В = 6, Г = 8; б) В = 7, Г = 10.
Из каждой вершины выпуклого многогранника выходит три
ребра. Сколько он имеет вершин и граней, если число ребер равно:
а) 12; б) 15?
Ответ: а) В = 8, Г = 6; б) В - 10, Г = 7.