TheSlide.ru

Презентация урока математики 6 класс "Осевая симметрия"

Содержание

1. Презентация урока математики 6 класс "Осевая симметрия"
2. СодержаниеСимметрияОсевая симметрияСимметрия в геометрии, природе, архитектуре, поэзииЗаключение
3. ОпределениеСимметрия (от греч. Symmetria – соразмерность), в
4. Осевая симметрияДве точки, лежащие на одном перпендикуляре
5. Фигура называется симметричной относительно прямой a, если
6. Фигуры, обладающие одной осью симметрииУголРавнобедренный треугольникРавнобедренная трапеция
7. Фигуры, обладающие двумя осями симметрииПрямоугольникРомб
8. Фигуры, имеющие более двух осей симметрииРавносторонний треугольникКвадратКруг
9. Фигуры, не обладающие осевой симметриейПроизвольный треугольникПараллелограммНеправильный многоугольник
10. Построениеточки, симметричной даннойотрезка, симметричного данномутреугольника, симметричного данному
11. Построение точки, симметричной даннойАсА’Определение1. АО⊥сО2. АО=ОА’
12. Построение отрезка, симметричного данномуАсА’ВВ’ОпределениеOO'АА’⊥с, АО=ОА’.ВВ’⊥с, ВО’=О’В’.3. А’В’ – искомый отрезок.
13. Построение треугольника, симметричного данномуАсА’ВВ’DD’Определение1. AA’⊥c AO=OA’2. BB’⊥c BO’=O’B’3. DD’⊥c DO”=O”D’4. ΔA’B’D’ – искомый треугольник.OO”O’
14. 1. Для каждого из случаев, представленных на
15. 2. Для каждого из случаев, представленных на
16. с3. Постройте треугольники, симметричные данным, относительно прямой с.сс
17. с4. Постройте треугольники, симметричные данным, относительно прямой с.сс
18. 11. Начертите две прямые а и b
19. ПодсказкаДля решения задачи рекомендуется сначала отметить точку
20. Симметрия в природе
21. В архитектуре
22. Пушкин А.С. «Медный всадник»…В гранит оделася Нева;Мосты повисли над водами;Темнозелеными садамиЕе покрылись острова…Симметрия в поэзии
23. Заключение Симметрию можно обнаружить почти везде, если знать,
24. Скачать презентанцию

СодержаниеСимметрияОсевая симметрияСимметрия в геометрии, природе, архитектуре, поэзииЗаключение

Главная
Математика
Презентация урока математики 6 класс "Осевая симметрия"

Слайды и текст этой презентации

Слайд 1Осевая симметрия

Осевая симметрия

Слайд 2Содержание
Симметрия
Осевая симметрия
Симметрия в геометрии, природе, архитектуре, поэзии
Заключение

СодержаниеСимметрияОсевая симметрияСимметрия в геометрии, природе, архитектуре, поэзииЗаключение

Слайд 3Определение
Симметрия (от греч. Symmetria – соразмерность), в широком смысле –

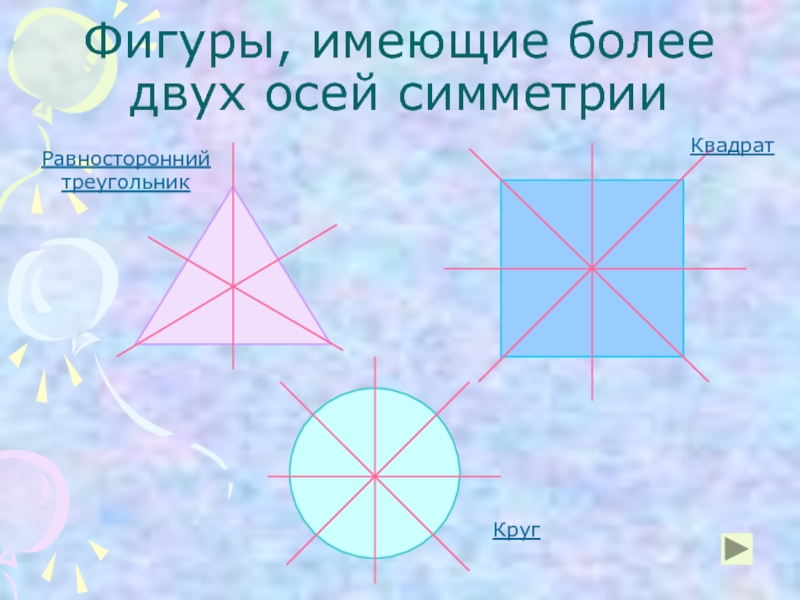
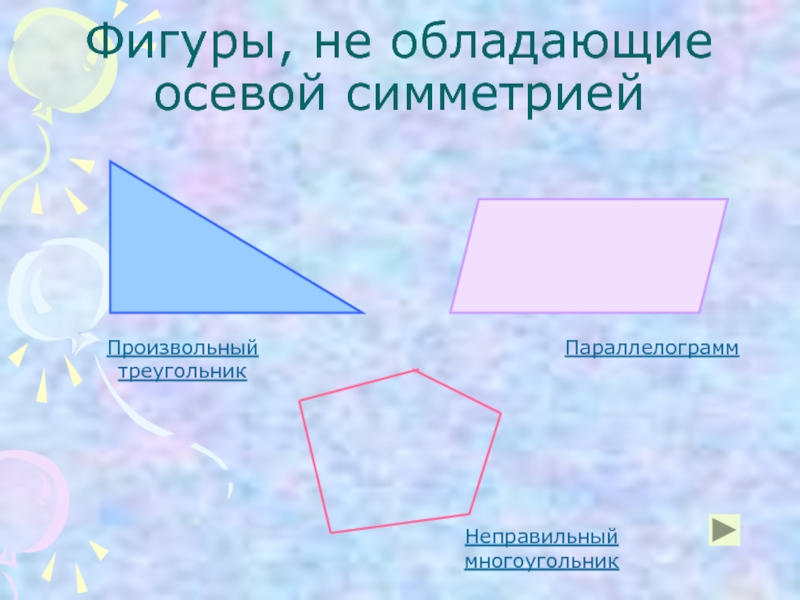
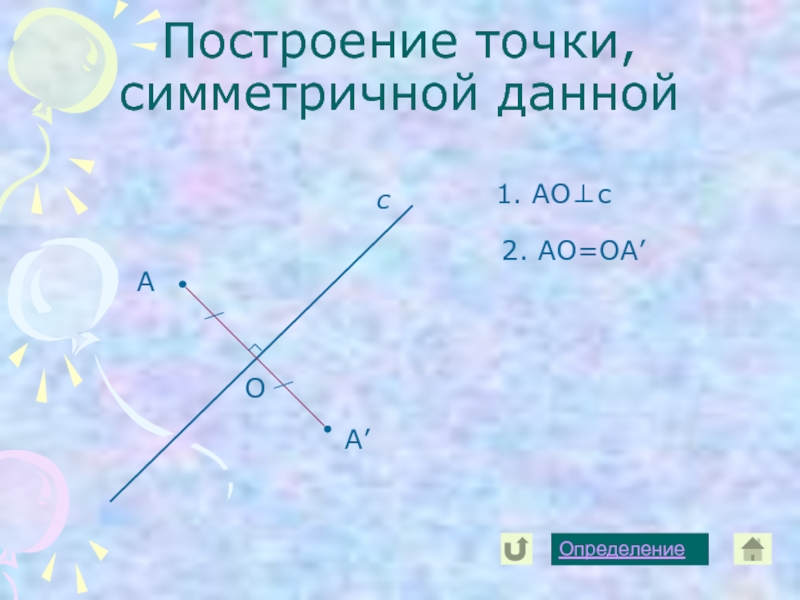
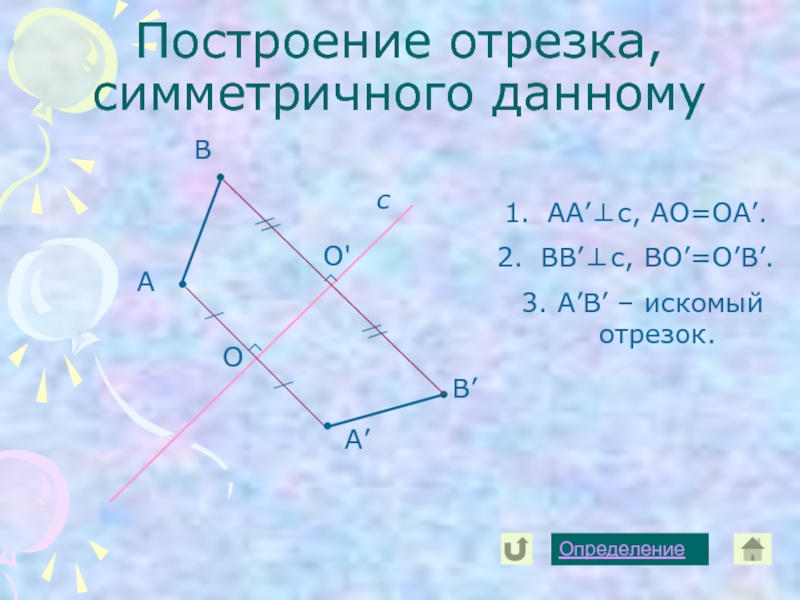
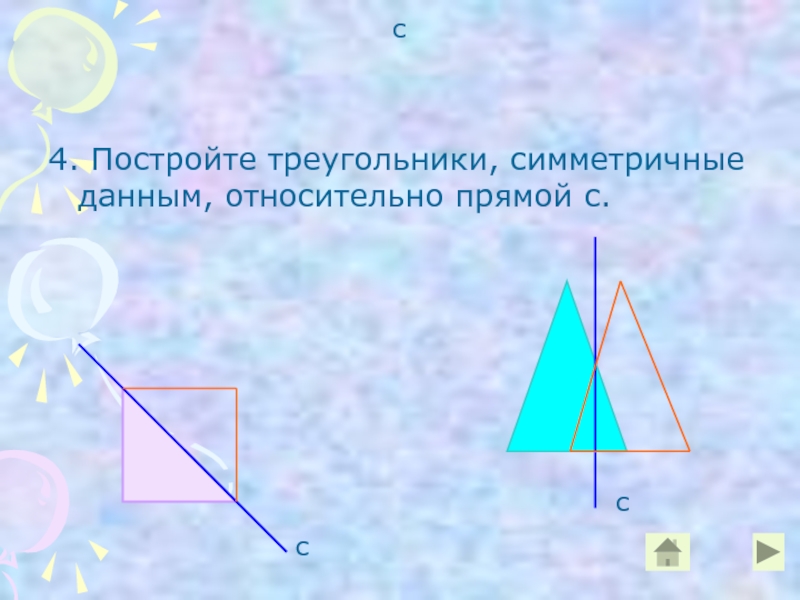
неизменность структуры материального объекта относительно его преобразований. Симметрия играет огромную

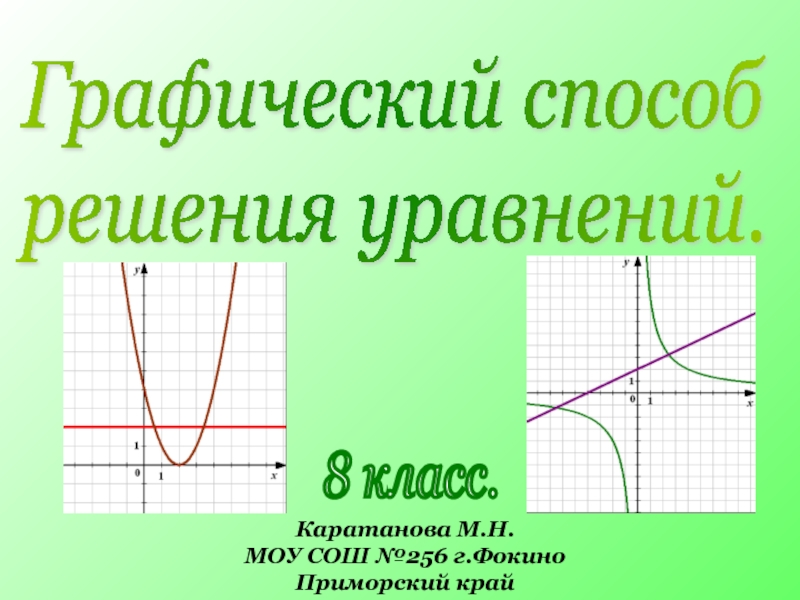
роль в искусстве и архитектуре. Но ее можно заметить и в музыке, и в поэзии. Симметрия широко встречается в природе, в особенности у кристаллов, у растений и животных. Симметрия может встретиться и в других разделах математики, например при построении графиков функций.

ОпределениеСимметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность структуры материального объекта относительно его преобразований.

Слайд 4Осевая симметрия
Две точки, лежащие на одном перпендикуляре к данной прямой

по разные стороны и на одинаковом расстоянии от нее, называются

симметричными относительно данной прямой.

Осевая симметрияДве точки, лежащие на одном перпендикуляре к данной прямой по разные стороны и на одинаковом расстоянии

Слайд 5Фигура называется симметричной относительно прямой a, если для каждой точки

фигуры симметричная ей точка относительно прямой а также принадлежит этой

фигуре.

а

Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой а

Слайд 6Фигуры, обладающие одной осью симметрии

Угол
Равнобедренный
треугольник
Равнобедренная трапеция

Фигуры, обладающие одной осью симметрииУголРавнобедренный треугольникРавнобедренная трапеция

Слайд 7Фигуры, обладающие двумя осями симметрии

Прямоугольник
Ромб

Фигуры, обладающие двумя осями симметрииПрямоугольникРомб

Слайд 8Фигуры, имеющие более двух осей симметрии

Равносторонний треугольник
Квадрат
Круг

Фигуры, имеющие более двух осей симметрииРавносторонний треугольникКвадратКруг

Слайд 9Фигуры, не обладающие осевой симметрией

Произвольный треугольник
Параллелограмм
Неправильный многоугольник

Фигуры, не обладающие осевой симметриейПроизвольный треугольникПараллелограммНеправильный многоугольник

Слайд 10Построение
точки, симметричной данной
отрезка, симметричного данному
треугольника, симметричного данному

Построениеточки, симметричной даннойотрезка, симметричного данномутреугольника, симметричного данному

Слайд 11Построение точки, симметричной данной

А
с

А’

Определение

1. АО⊥с
О
2. АО=ОА’

Построение точки, симметричной даннойАсА’Определение1. АО⊥сО2. АО=ОА’

Слайд 12Построение отрезка, симметричного данному
А
с

А’

В
В’
Определение

O
O'
АА’⊥с, АО=ОА’.
ВВ’⊥с, ВО’=О’В’.
3. А’В’ – искомый отрезок.

Построение отрезка, симметричного данномуАсА’ВВ’ОпределениеOO'АА’⊥с, АО=ОА’.ВВ’⊥с, ВО’=О’В’.3. А’В’ – искомый отрезок.

Слайд 13Построение треугольника, симметричного данному
А
с

А’

В
В’
D

D’
Определение

1. AA’⊥c AO=OA’
2. BB’⊥c BO’=O’B’
3. DD’⊥c

DO”=O”D’
4. ΔA’B’D’ – искомый треугольник.
O
O”
O’

Построение треугольника, симметричного данномуАсА’ВВ’DD’Определение1. AA’⊥c AO=OA’2. BB’⊥c BO’=O’B’3. DD’⊥c DO”=O”D’4. ΔA’B’D’ – искомый треугольник.OO”O’

Слайд 141. Для каждого из случаев, представленных на рисунке, постройте точки

А' и В', симметричные точкам А и В относительно прямой

с.

В

А

с

А

В

с

А

В

с

1. Для каждого из случаев, представленных на рисунке, постройте точки А' и В', симметричные точкам А и

Слайд 152. Для каждого из случаев, представленных на рисунке, постройте точки

А' и В', симметричные точкам А и В относительно прямой

с.

В

В'

А

А'

с

А

А'

В

В'

с

А

В

с

А'

В'

2. Для каждого из случаев, представленных на рисунке, постройте точки А' и В', симметричные точкам А и

Слайд 16с
3. Постройте треугольники, симметричные данным, относительно прямой с.

с

с

с3. Постройте треугольники, симметричные данным, относительно прямой с.сс

Слайд 17с
4. Постройте треугольники, симметричные данным, относительно прямой с.

с

с

с4. Постройте треугольники, симметричные данным, относительно прямой с.сс

Слайд 1811. Начертите две прямые а и b и отметьте две

точки А и В так, чтобы точка С была симметрична

точке А относительно прямой а, а точке В относительно прямой b.

11. Начертите две прямые а и b и отметьте две точки А и В так, чтобы точка

Слайд 19Подсказка
Для решения задачи рекомендуется сначала отметить точку С, а лишь

потом отмечать точки А и В.

ПодсказкаДля решения задачи рекомендуется сначала отметить точку С, а лишь потом отмечать точки А и В.

Слайд 20Симметрия в природе

Симметрия в природе

Слайд 21В архитектуре

В архитектуре

Слайд 22Пушкин А.С. «Медный всадник»
…В гранит оделася Нева;
Мосты повисли над водами;
Темнозелеными

садами
Ее покрылись острова…

Симметрия в поэзии

Пушкин А.С. «Медный всадник»…В гранит оделася Нева;Мосты повисли над водами;Темнозелеными садамиЕе покрылись острова…Симметрия в поэзии

Слайд 23Заключение
Симметрию можно обнаружить почти везде, если знать, как ее искать.

Многие народы с древнейших времен владели представлением о симметрии в

широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».

Заключение Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей