Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комбинаторика
Содержание
- 1. Комбинаторика
- 2. Усний рахунок
- 3. Задача 1. Жителі планети Кін-дза-дза обходилися для
- 4. Задача 2. У жителів планети АХО в
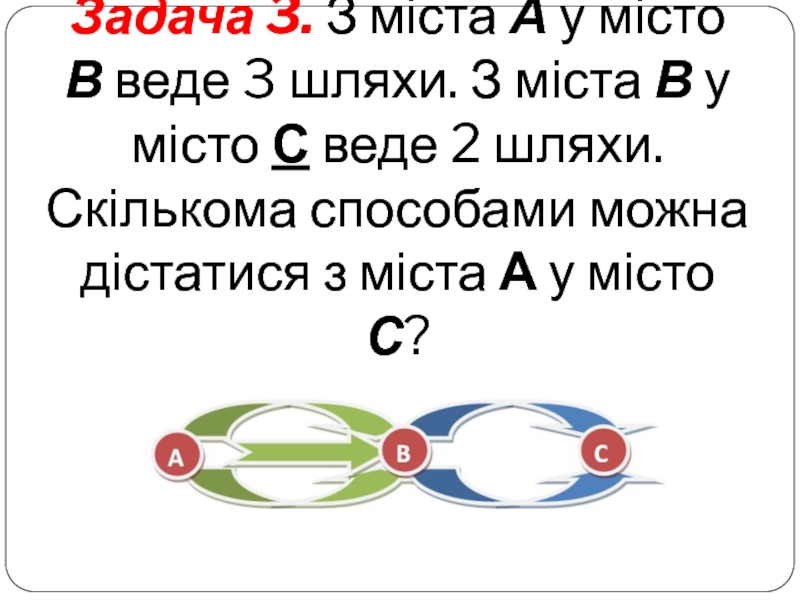
- 5. Задача 3. З міста А у місто
- 6. Основне правило комбінаторики. Нехай є дві дії,
- 7. Задача 4. На вершину гори веде 7
- 8. Задача 5. Квартет.
- 9. ФІЗКУЛЬТХВИЛИНКА
- 10. Правило множення. Кількість способів Р якими ми
- 11. Задача 6. Скільки двозначних чисел можна скласти, використовуючи цифри 1, 7, 4 (цифри можуть повторюватись)
- 12. Задача 7. Скільки двозначних чисел можна скласти, використовуючи цифри 9, 7, 0 (цифри можуть повторюватись)
- 13. Задача 8. У класі 25 учнів, скількома способами можна обрати командира класу та його заступника?
- 14. Задача 9. У розіграші першості країни з
- 15. Домашнє завдання. Конспект Творче завдання: скласти
- 16. Урок-презентацію розробила Пономаренко О.О., вчитель математики Красноармійського навчально-виховного комплексу
- 17. Скачать презентанцию
Усний рахунок
Слайды и текст этой презентации
Слайд 4Задача 2. У жителів планети АХО в алфавіті три букви:
А, О, Х. Слова в мові складаються з трьох букв.
Яку найбільшу кількість слів може бути в словнику жителів цієї планети? (Букви в словах повторюватись не повинні)
Слайд 5Задача 3. З міста А у місто В веде 3
шляхи. З міста В у місто С веде 2
шляхи. Скількома способами можна дістатися з міста А у місто С?
Слайд 6Основне правило комбінаторики. Нехай є дві дії, причому першу дію
можна виконати n способами, а другу дію можна виконати m
способами, тоді послідовність дій: спочатку першої, а потім другої можна виконати n•m способами
Слайд 7Задача 4. На вершину гори веде 7 стежок. Скількома способами
турист може піднятися і спуститися
з гори?
А якщо різними
шляхами?
Слайд 10Правило множення. Кількість способів Р якими ми можемо заповнити 1
позицію дорівнює максимальній кількості способів n, 2 позицію – n-1
(оскільки перший елемент вже займає одне місце), …, останню – одним способом. Згідно основному правилу комбінаторики перемножимо P=n(n-1)•…•1
Слайд 11Задача 6. Скільки двозначних чисел можна скласти, використовуючи цифри 1,
7, 4 (цифри можуть повторюватись)
Слайд 12Задача 7. Скільки двозначних чисел можна скласти, використовуючи цифри 9,
7, 0 (цифри можуть повторюватись)
Слайд 13Задача 8. У класі 25 учнів, скількома способами можна обрати
командира класу та його заступника?
Слайд 14Задача 9. У розіграші першості країни з футболу бере участь
16 команд. Скількома способами можуть бути розподілені золота і срібна
медалі?
Слайд 15Домашнє завдання. Конспект Творче завдання: скласти та оформити задачу з
комбінаторики з розв'язком
Дякую за роботу!
Слайд 16Урок-презентацію розробила Пономаренко О.О.,
вчитель математики Красноармійського навчально-виховного комплексу
