Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентатция "Показательная функция"
Содержание
- 1. Презентатция "Показательная функция"
- 2. *ПланВведениеОпределение показательной функцииСвойства показательной функцииПостроение графиков функцийПрименение
- 3. *ВведениеФункция - одно из основных математических и
- 4. *Определение показательной функцииФункция, заданная формулой у=а x
- 5. * Отработка определения. Почему а>0?При а
- 6. *Свойства функцииСхема:Область определения функцииОбласть значений функцииЧетность или
- 7. *Свойства показательной функцииОбласть определения: множество всех действительных
- 8. *Применение показательной функцииприродеэкономикефизикепроизводствеЗапишите в тетрадь
- 9. * Рост и размножение бактерий Рост бактериальной
- 10. *БиологияВ питательной среде бактерия кишечной палочки делится
- 11. * Примером быстрого размножения бактерий является процесс
- 12. *Легенда В древней легенде об изобретателе
- 13. *Формула сложного процентного ростаp - % годовыхS
- 14. *ЭкономикаПодсчитаем, сколько денег получит вкладчик, скажем, через
- 15. *ФизикаВсе, наверное, замечали, что если снять кипящий
- 16. *tNOРаспад большого количества ядер любого радиоактивного изотопа
- 17. *Задача:Период полураспада плутония равен 140 суткам. Сколько
- 18. *Численность популяции составляет 5 тыс. особей. За
- 19. * В производстве Лесной участок содержит 6500
- 20. *Показательные уравнения Показательным называется уравнение,
- 21. *Запишите в тетрадьМетоды решения уравнений
- 22. * Приведение степеней к одному основанию Запишите в тетрадь
- 23. *Вынесение общего множителя за скобкиЗапишите в тетрадь
- 24. * Замена переменной Запишите в тетрадь9x-4.
- 25. * Почленное деление Запишите в
- 26. *Метод группировки Запишите в тетрадь
- 27. *Графический способЗапишите в тетрадьРешить графически уравнение:2-x=3x+10.Решение.Пусть y=2-x
- 28. *Графический способЗапишите в тетрадь2) Ответ: 2.Решение.Пусть y=или
- 29. *Графический способЗапишите в тетрадь3) 2x=3-2x-x2.Решение.Построим графики функций
- 30. *Запишите в тетрадь4) 3-x=Решение.Построим графики функций при
- 31. *Показательные неравенстваЗапишите в тетрадьПростейшими показательными неравенствами являются неравенствавида:ax>ac и ax>b,a>0,a≠1,b>0. Если Если
- 32. *Показательные неравенстваЗапишите в тетрадь
- 33. *Показательные неравенстваЗапишите в тетрадь
- 34. *Показательные неравенстваЗапишите в тетрадь
- 35. *Построение графиков функцийПостроить график функции:1) .Решение.Из определения модуля следует, чтоЗапишите в тетрадь
- 36. *Построение графиков функций . Запишите в тетрадь
- 37. *Решение систем уравненийЗапишите в тетрадь
- 38. *Решение систем уравненийЗапишите в тетрадь
- 39. *Ресурсыmoumk.ucoz.rumoumk.ucoz.ru › …primenenie_pokazatelnoj_funkcii…10 school.baltinform.ruschool.baltinform.ru › files/3/documents_13266_festival.1september.rufestival.1september.ru ›
- 40. *ЛитератураН.Я. Виленкин «Алгебра и математический анализ для 11
- 41. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Бекетова Татьяна Зелимхановна, преподаватель математики
ГБПОУ «Минераловодский региональный многопрофильный колледж»
ПОКАЗАТЕЛЬНАЯ
ФУНКЦИЯ
Слайд 2*
План
Введение
Определение показательной функции
Свойства показательной функции
Построение графиков функций
Применение показательной функции
Показательные уравнения
Способы
решения показательных уравнений
Показательные неравенства
Решение систем показательных уравнений
Ресурсы
Литература
Слайд 3*
Введение
Функция - одно из основных математических и общенаучных понятий. Оно
сыграло и поныне играет большую роль в познании реального мира. Идея
функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур.Функция- это основной математический инструмент для изучения связей, зависимостей между различными величинами. Чем большим запасом функций мы располагаем, тем шире и богаче наши возможности математического описания окружающего мира. С примерами быстро растущих функций человек столкнулся очень давно. Однако лишь с конца 17 в. стали систематически рассматриваться зависимости типа у = сּg x, в которых переменная x принимает не только целые значения.
Слайд 4*
Определение показательной функции
Функция, заданная формулой у=а x (где а>0, a≠1),
называется показательной функцией с основанием а
Запишите в тетрадь
Слайд 5*
Отработка определения.
Почему а>0?
При а
не имеет смысла
выражение (-7)½.Почему а≠1?
1̽ = 1 при любом х.
Почему а ≠ 0?
0̽ = 0, 0° не имеет смысла.
Запишите в тетрадь
Слайд 6*
Свойства функции
Схема:
Область определения функции
Область значений функции
Четность или нечётность функции
Нули функции
Промежутки
знакопостоянства функции
Монотонность функции
Экстремумы
Ограниченность функции
Непрерывность
Слайд 7*
Свойства показательной функции
Область определения: множество всех действительных чисел, D (y)=R
Область
значений: множество всех положительных чисел, E (y)=R+
Функция ни четная, ни
нечетнаяНулей функции нет
Не ограничена сверху, ограничена снизу
Показательная функция у=ах является возрастающей на множестве всех действительных чисел,если а>1,и убывающей,если 0<а<1
Не имеет ни наибольшего, ни наименьшего значения
Непрерывна
Если а>1 ,то функция выпукла вниз
Запишите в тетрадь
Слайд 9*
Рост и размножение бактерий
Рост бактериальной клетки — это увеличение
объема одной особи между двумя делениями. Молодая
клетка увеличивается, удлиняется. Когда она достигает определенной длины, то образуется перегородка перпендикулярно ее длине. Перегородка расщепляется надвое, и получаются две дочерние клетки , чаще одинакового размера. При благоприятных условиях деление клеток совершается очень быстро, через каждые 20—30 минут, у термофилов, даже через 5 минут, у кислотоупорных гораздо медленнее, 1мор у туберкулезной палочки через 19 часов. Микобактерии размножаются не только делением, но и почкованием. Теоретически рассуждая бактерии могут размножаться беспредельно. Так, подсчитано, что при делении одной клетки через каждые 20 минут за 24 часа получилось бы 72 генерации и образовалось бы 472 • 1019 клеток. Если считать, что один миллиард клеток весит 1 мг, то 472ּ1019 клеток будут весить 4720 тонн. Через несколько дней микробные клетки заполнили бы все моря и океаны на Земле. Но этого не происходит, так как в природе нет соответствующих условий. Большая скорость размножения бактерий содействует сохранению их на Земле, так как у многих из них отсутствуют особые защитные приспособления, что могло бы привести их к быстрому вымираниюЗапишите в тетрадь
Слайд 10*
Биология
В питательной среде бактерия кишечной палочки делится каждую минуту. Понятно,
что общее число бактерий за каждую минуту удваивается. Если в
начале процесса была одна бактерия, то через х минут их число (N) станет равной 2х , т.е. N(х) = 2хЗапишите в тетрадь
Слайд 11*
Примером быстрого размножения бактерий является процесс изготовления дрожжей, при
котором по мере их роста производится соответствующая добавка перерабатываемой сахаристой
массы. Увеличение массы дрожжей выражается показательной функцией:где первоначальная масса дрожжей,
t – время дрожжевания в часах,
m – масса дрожжей в процессе дрожжевания.
Вычислим m, если 10 кг и t = 9 ч.
Решение. Вычислим массу дрожжей в процессе дрожжевания:
Ответ: масса полученных дрожжей:
Задача
Запишите в тетрадь
Слайд 12*
Легенда
В древней легенде об изобретателе шахмат говорится, что
он потребовал за первую клетку шахматной доски одно пшеничное зерно,
а за каждую следующую — вдвое больше, чем за предыдущую. Человеку трудно представить себе порядок величины 2664-1 (общее число зерен, плату за изобретение шахмат). Если грубо заменить210 = 1024 на 103, то 264 = 24 . 260=16. 1018=1,6.1019. Достаточно сказать, что расстояние от Земли до Солнца в миллиметрах приблизительно равно 1,5ּ1014 , так что, считая диаметр зерна за 1 мм, можно этим зерном 100 тысяч раз уложить путь до Солнца.
Запишите в тетрадь
Слайд 13*
Формула сложного процентного роста
p - % годовых
S - внесенная сумма
Sn
- сумма, которая будет на счёте через n лет
Запишите в
тетрадьСлайд 14*
Экономика
Подсчитаем, сколько денег получит вкладчик, скажем, через 3 года, если
он положил на счёт в банк 1500 р. И ни
разу не будет брать деньги со счёта, а тем временем сумма будет ежегодно увеличиваться на 10%:10% от этой суммы составляют 0,1 *1500 = 150р
через год на счёте будет
1500 + 150 = 1650 р.
10% от новой суммы составляют 0,1 * 1650 = 165 р.,
через два года на счёте будет
1650 + 165 = 1815 р.
10% от новой суммы составляют 0,1 * 1815 = 181,5 р.,
через три года на счёте будет
1815 + 181,5 = 1996,5 р.
Запишите в тетрадь
Слайд 15*
Физика
Все, наверное, замечали, что если снять кипящий чайник с огня,
то сначала он быстро остывает, а потом остывание идет гораздо
медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой:T=(T1-T0)e-kt+T1,
где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.
Запишите в тетрадь
Слайд 16*
t
N
O
Распад большого количества ядер любого радиоактивного изотопа подчиняется одному закону,
который может быть выражен в следующей математической форме:
N=N0. 2Это уравнение носит название закона радиоактивного распада. В нем N0 означает начальное количество радиоактивных ядер в момент времени, с которого начинаются наблюдения (t=0). Число ядер, не испытавших распада до некоторого произвольного момента времени t, обозначено N. Символом Tобозначена постоянная величина, зависящая от типа радиоактивного изотопа. Эта постоянная называется периодом полураспада. Через промежуток времени, равный периоду полураспада (t=T), исходное количество радиоактивных ядер убывает вдвое. На рисунке по оси ординат отложено количество радиоактивных ядер в момент времени t, время отсчитывается по оси абсцисс.
T
2T
Закон радиоактивного распада
Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.
Запишите в тетрадь
Слайд 17*
Задача:
Период полураспада плутония равен 140 суткам. Сколько плутония останется через
10 лет, если его начальная масса равна 8г ?
m =
?Ответ: 1,13•10-7 (г).
Запишите в тетрадь
Слайд 18*
Численность популяции составляет 5 тыс. особей. За последнее время в
силу разных причин (браконьерство, сокращение ареалов обитания) она ежегодно сокращалась
на 8%. Через сколько лет (если не будут предприняты меры по спасению данного вида и сохранятся темпы его сокращения) численность животных достигнет предела – 2 тыс. особей, за которым начнётся вымирание этого вида?Решение. Применим для вычисления времени формулу сложных процентов:
где
2 тыс. – численность животных по истечению искомого времени;
5 тыс. – численность животных в начальный момент времени;
p = 8 - % сокращения численности животных.
Предварительно разделив обе части уравнения на 1000, получим:
лет.
Ответ: приблизительно через 11 лет.
В производстве
Запишите в тетрадь
Слайд 19*
В производстве
Лесной участок содержит 6500 м3 древесины.
Сколько будет древесины
на этом участке через 10
лет, если ежегодный прирост леса
составляет в среднем 2% ?
Найдем, сколько древесины будет в лесу через 10
лет по формуле сложных процентов:
S – результат;
A – исходное кол-во товара;
p – процент увеличения;
n – кол-во лет.
S = A· (1 + p/100)n
S = 6500· (1 +2/100)10 ≈ 7923,46 м3
Запишите в тетрадь
Слайд 20*
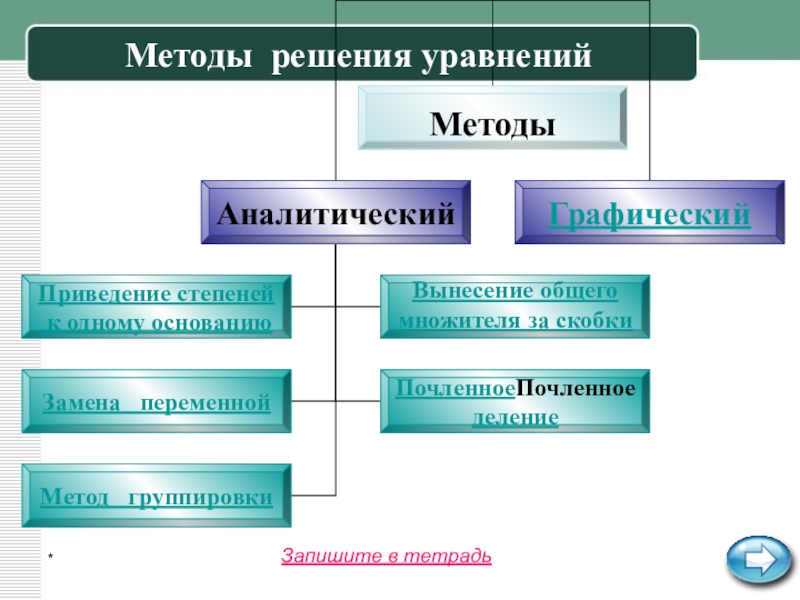
Показательные уравнения
Показательным называется уравнение, содержащее переменную в показателе
степени.
Простейшими показательными уравнениями являются уравнения вида:
ax=ac и ax=b,a>0,a≠1,b>0.
Если
ax=ac, то x=c является решением этого уравнения, его корнем.Если ax=b, то x=logab- корень этого уравнения.
Запишите в тетрадь
Слайд 24*
Замена переменной
Запишите в тетрадь
9x-4. 3x+3=0.
Решение.
9x-4. 3x+3=0,
32x-4.
3x+3=0,
Уравнение квадратное оносительно 3x=y.
Имеем уравнение y2-4y+3=0.
Корни y1=1; y2=3.
Перейдем к переменной
x.При y1=1 имеем 3x=1, 3x=30,x1=0,
при y2=3 имеем 3x=3, x2 =1.
Ответ: 0; 1.
Слайд 25*
Почленное деление
Запишите в тетрадь
5x = 8x.
Решение.
Разделим обе
части уравнения на 8x
0
x=0.
Ответ: 0.
Слайд 27*
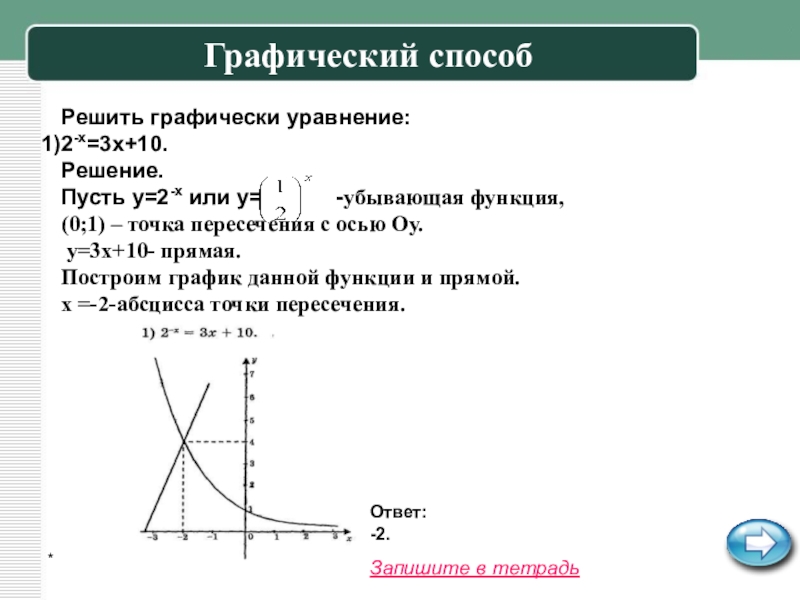
Графический способ
Запишите в тетрадь
Решить графически уравнение:
2-x=3x+10.
Решение.
Пусть y=2-x или y=
-убывающая функция,
(0;1) – точка пересечения
с осью Oy.y=3x+10- прямая.
Построим график данной функции и прямой.
x =-2-абсцисса точки пересечения.
Ответ: -2.
Слайд 28*
Графический способ
Запишите в тетрадь
2)
Ответ: 2.
Решение.
Пусть y=
или y=3x -возрастающая
функция, (0;1)- точка пересечения с осью Oy,
y=2x+5-прямая. Построим график
данной функции и прямой.x=2- абсцисса точки пересечения.
Слайд 29*
Графический способ
Запишите в тетрадь
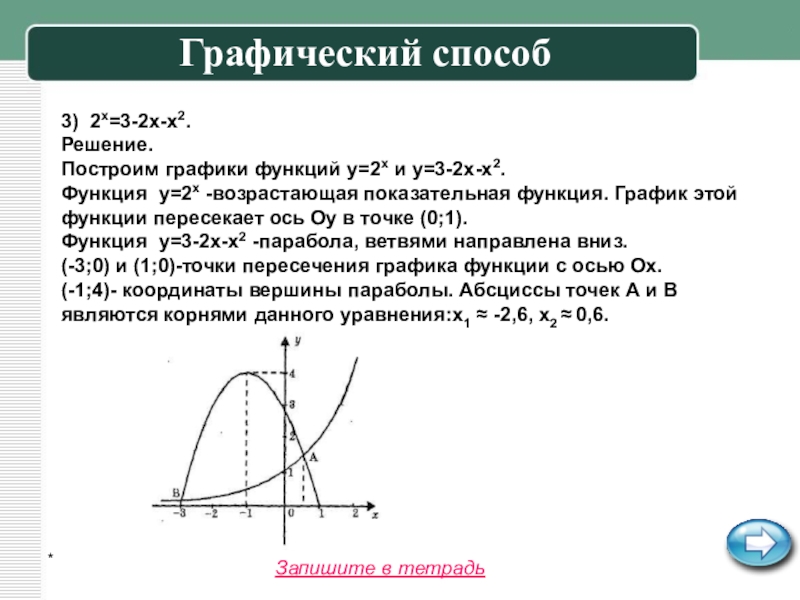
3) 2x=3-2x-x2.
Решение.
Построим графики функций y=2x и y=3-2x-x2.
Функция y=2x -возрастающая показательная функция. График этой функции пересекает ось
Oy в точке (0;1). Функция y=3-2x-x2 -парабола, ветвями направлена вниз.
(-3;0) и (1;0)-точки пересечения графика функции с осью Ox.
(-1;4)- координаты вершины параболы. Абсциссы точек А и В являются корнями данного уравнения:x1 ≈ -2,6, x2 ≈ 0,6.
Слайд 30*
Запишите в тетрадь
4) 3-x=
Решение.
Построим графики функций
при
Абсцисса точки
пересечения этих графиков x=
- корень данного уравнения.
Графический способ
Слайд 31*
Показательные неравенства
Запишите в тетрадь
Простейшими показательными неравенствами являются неравенства
вида:
ax>ac и ax>b,a>0,a≠1,b>0.
Если
Если
Слайд 35*
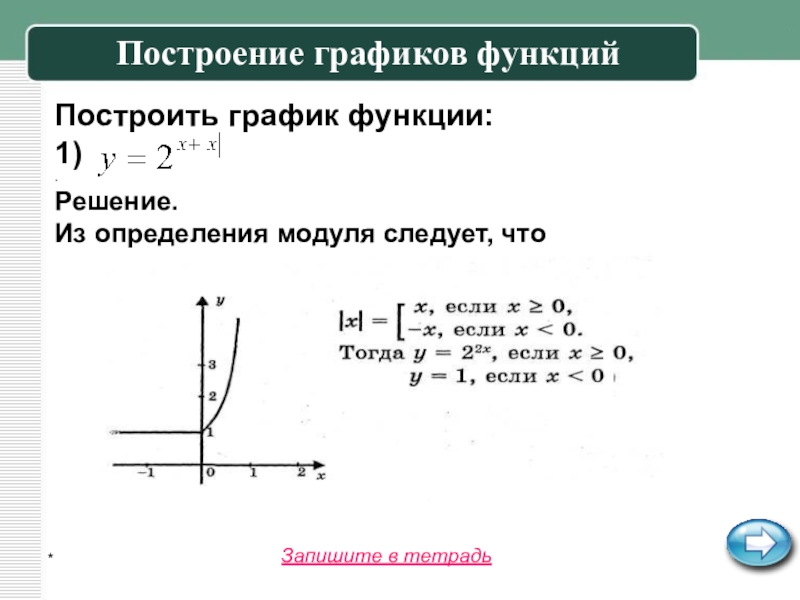
Построение графиков функций
Построить график функции:
1)
.
Решение.
Из определения модуля следует, что
Запишите
в тетрадь
Слайд 39*
Ресурсы
moumk.ucoz.rumoumk.ucoz.ru › …primenenie_pokazatelnoj_funkcii…10
school.baltinform.ruschool.baltinform.ru › files/3/documents_13266_
festival.1september.rufestival.1september.ru › articles/567461/
revolution.allbest.rurevolution.allbest.ru›Педагогикаrevolution.allbest.ru›Педагогика›00181238_0.html
musoch50.narod.rumusoch50.narod.ru
› otkr_uroki/morojoba_2.doc
lawrencenko.rulawrencenko.ru › files/calc1-l13-lawrencenko.pdf
mathem.by.rumathem.by.ru › kompl6.html
sh10-borisov.narod.rush10-borisov.narod.ru ›
urok/matem8.pdf zavuch.infozavuch.info › component/mtree/tochnie/algebra/…
Слайд 40*
Литература
Н.Я. Виленкин «Алгебра и математический анализ для 11 класса»,М., «Просвещение», 1990
г.
Севрюков П.Ф. Тригонометрические, показательные и логарифмические уравнения и неравенства: учебное
пособие. Изд. 2 доп./П.Ф. Севрюков, А.Н. Смоляков.-М.: Илекса;Народное образование;Ставрополь:Сервисшкола,2010.-396с.-(Серия «Изучение сложных тем школьного курса математики»).А.Н. Колмогоров «Алгебра и начала анализа, 10–11», М., «Просвещение», 2001 г.
Мордкович А.Г. «Алгебра и начала анализа. 10–11 класс», М., «Мнемозина», 2001г.
Алимов Ш.А., Колягин Ю.М. Сидоров Ю.В, «Алгебра и начала анализа», учебник для 10–11 классов общеобразовательных, Просвещение 2003г.
Р.А. Погосьян «Алгебра и начала анализа. 10 кл.».-Ростов н/Д.:Изд-во «Феникс», 1996г.



 0, a≠1), называется" alt="*Определение показательной функцииФункция, заданная формулой у=а x (где а>0, a≠1), называется показательной функцией с основанием аЗапишите в">
0, a≠1), называется" alt="*Определение показательной функцииФункция, заданная формулой у=а x (где а>0, a≠1), называется показательной функцией с основанием аЗапишите в"> 0?При а" alt="* Отработка определения. Почему а>0?При а">
0?При а" alt="* Отработка определения. Почему а>0?При а">





















 ac и ax>b,a>0,a≠1,b>0. Если Если" alt="*Показательные неравенстваЗапишите в тетрадьПростейшими показательными неравенствами являются неравенствавида:ax>ac и ax>b,a>0,a≠1,b>0. Если Если">
ac и ax>b,a>0,a≠1,b>0. Если Если" alt="*Показательные неравенстваЗапишите в тетрадьПростейшими показательными неравенствами являются неравенствавида:ax>ac и ax>b,a>0,a≠1,b>0. Если Если">