Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применения производной к исследованию функций
Содержание
- 1. Применения производной к исследованию функций
- 2. ОглавлениеСхема исследования функций;Признак возрастания (убывания) функции:Достаточный признак
- 3. Схема исследования функцийНайти области определения и значений
- 4. Признак возрастания (убывания) функции
- 5. Достаточный признак возрастания функции. Если f´ (x)
- 6. Доказательство признака возрастания (убывания) функции Доказательство проводится на основании формулы Лагранжа: f´
- 7. Пример нахождения промежутков возрастания (убывания) функцииДано: f
- 8. Критические точки функции, максимумы и минимумы
- 9. Необходимое условие экстремума (теорема Ферма) Если
- 10. Теорема Ферма есть лишь необходимое условие экстремума.
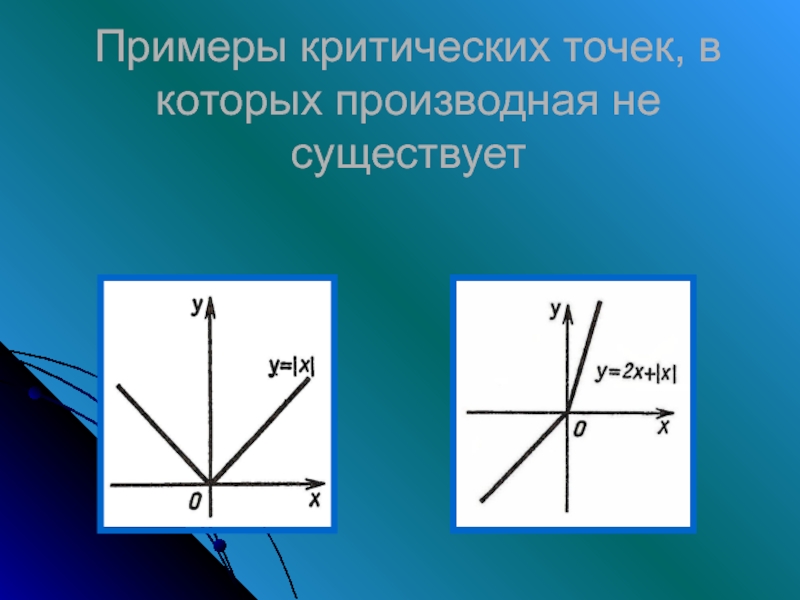
- 11. Примеры критических точек, в которых производная не существует
- 12. Признак максимума функции Если функция f
- 13. Признак минимума функции Если функция f
- 14. Пример нахождения точек экстремума функцииДано:f (x) =
- 15. Проект выполняла Сергеева Вероника, ученица 11 класса,
- 16. Скачать презентанцию
ОглавлениеСхема исследования функций;Признак возрастания (убывания) функции:Достаточный признак возрастания функции;Достаточный признак убывания функции;Критические точки функции:Необходимое условие экстремума;Признак максимума функции;Признак минимума функции.
Слайды и текст этой презентации
Слайд 2Оглавление
Схема исследования функций;
Признак возрастания (убывания) функции:
Достаточный признак возрастания функции;
Достаточный признак
убывания функции;
Слайд 3Схема исследования функций
Найти области определения и значений данной функции f.
Выяснить,
обладает ли функция особенностями, облегчающими исследование.
Вычислить координаты точек пересечения графика
с осями координат.Найти промежутки знакопостоянства функции f.
Выяснить, на каких промежутках функция f возрастает, а на каких убывает.
Найти точки и вид экстремума и вычислить значения f в этих точках.
Исследовать поведение функции f в окрестности характерных точек, не входящих в область определения.
Слайд 5Достаточный признак возрастания функции. Если f´ (x) > 0 в
каждой точке интервала I, то функция возрастает на I.
Достаточный признак
убывания функции. Если f´ (х) < 0 в каждой точке интервала I, то функция убывает на I.Слайд 6Доказательство признака возрастания (убывания) функции
Доказательство проводится на основании
формулы Лагранжа:
f´
Слайд 7Пример нахождения промежутков возрастания (убывания) функции
Дано:
f (x) = -2x
+ sin x
Найти:
промежутки возрастания (убывания) функции
Решение
Функция определена на всей числовой
прямой.Найдем f´ (x). f´ (x) = -2 + cos x.
| cos x | ≤ 1 => f´ (x) < 0 для всех действительных х.
Вывод: f (x) = -2x + sin x убывает на всей числовой прямой
Слайд 9Необходимое условие экстремума (теорема Ферма)
Если точка х0 является
точкой экстремума функции f и в этой точке существует производная
f´, то она равна нулю: f´(х0) = 0Слайд 10 Теорема Ферма есть лишь необходимое условие экстремума. Из того, что
производная в точке х0 обращается в нуль, необязательно следует, что
в этой точке функция имеет экстремум.Слайд 12Признак максимума функции
Если функция f непрерывна в точке
х0, а f´ (х) > 0 на интервале (а; х0)
и f´ (х) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f.Упрощённая формулировка признака:
Если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
Слайд 13Признак минимума функции
Если функция f непрерывна в точке
х0, f´ (х) < 0 на интервале (а; х0) и
f´ (х) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f.Упрощённая формулировка признака:
Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка максимума.
Слайд 14Пример нахождения точек экстремума функции
Дано:
f (x) = 3x – x3
Найти:
Точки
экстремума функции
Решение
Найдём производную функции: f´ (x) = 3 – 3х2
f´
(x) = 0, при х = 1 и х = -1f´ (x) < 0 при х < -1; f‘ (x) > 0 при -1 < х < 1, т.е. в точках -1 и 1 функция меняет знак.
По признакам максимума и минимума точка -1 является точкой минимума, а точка 1 — точкой максимума.