Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признак параллельности прямой и плоскости
Содержание
- 1. Признак параллельности прямой и плоскости
- 2. Это мы знаемПредстоитузнать
- 3. Это мы знаемПрямая и плоскость в пространствеКакие варианты расположения плоскости и прямой мы изучили?
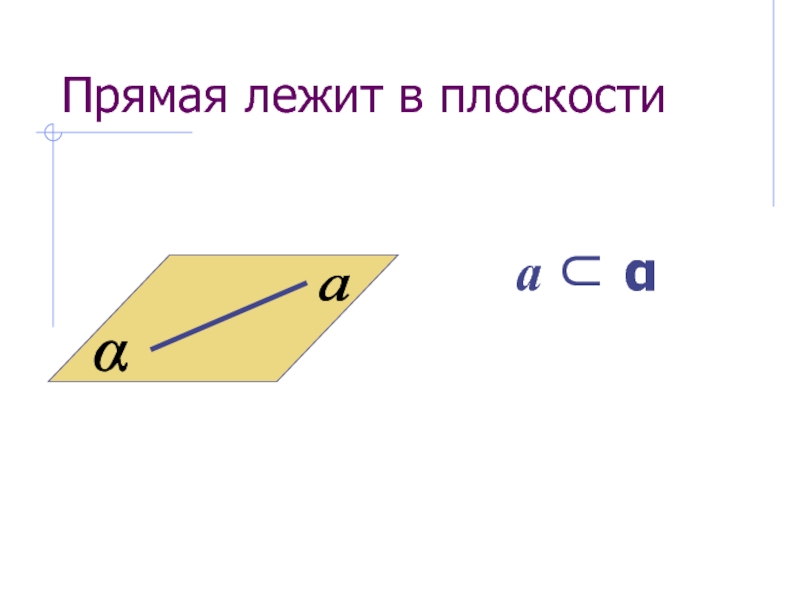
- 4. Прямая лежит в плоскостиa аα
- 5. Прямая не лежит в плоскостиa ∩ = Мααa || ааM
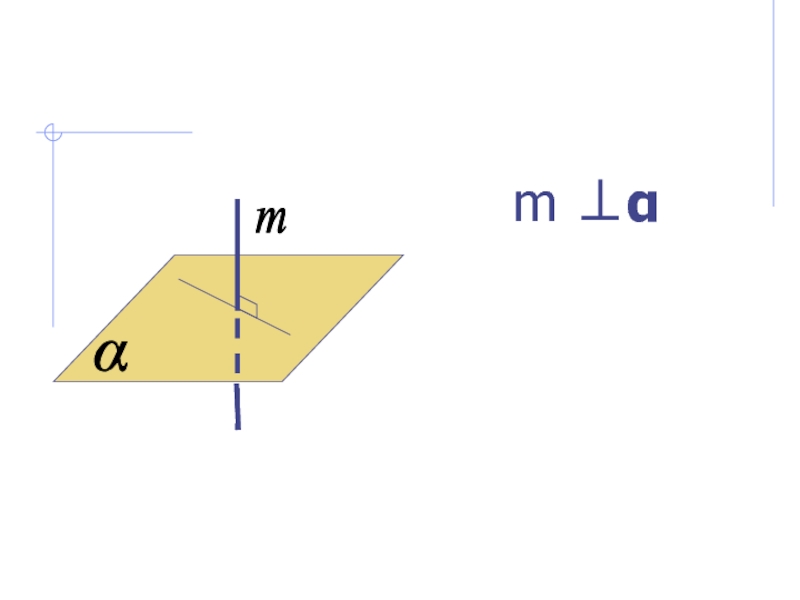
- 6. m mα
- 7. Вспомним план изучения темыОпределениеПризнакиСвойстваЗадачи на построениеПрименение к решению задач разного типа
- 8. Каково взаимное расположение двух плоскостей в пространстве?
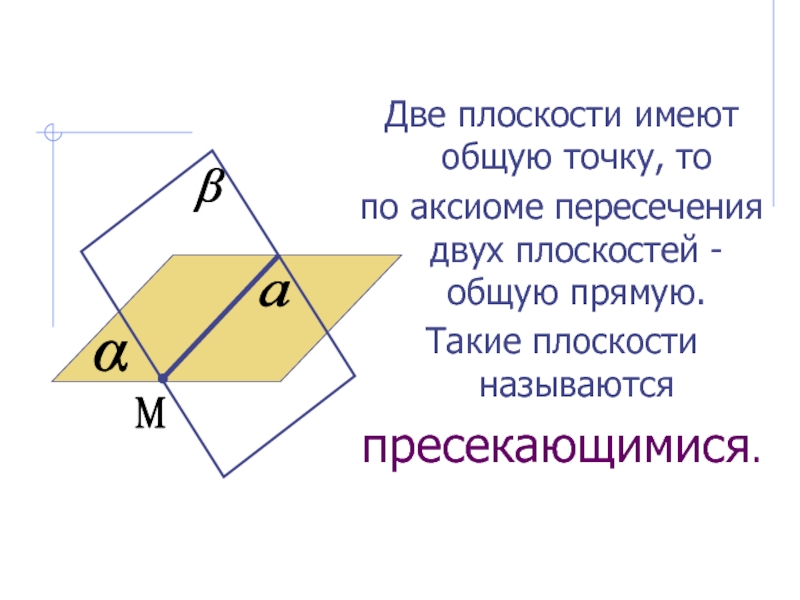
- 9. Две плоскости имеют общую точку, то по
- 10. Две плоскости не имеют общей точки. Такие плоскости называются параллельными. ||β αβ
- 11. Это мы изучим сегодняПараллельность плоскостей
- 12. План изучения темы:Определение параллельных плоскостейПризнакиСвойства параллельных плоскостейПрименение при решении задач
- 13. Определение.Две плоскости, не имеющие общей точки, называются параллельными. ||β
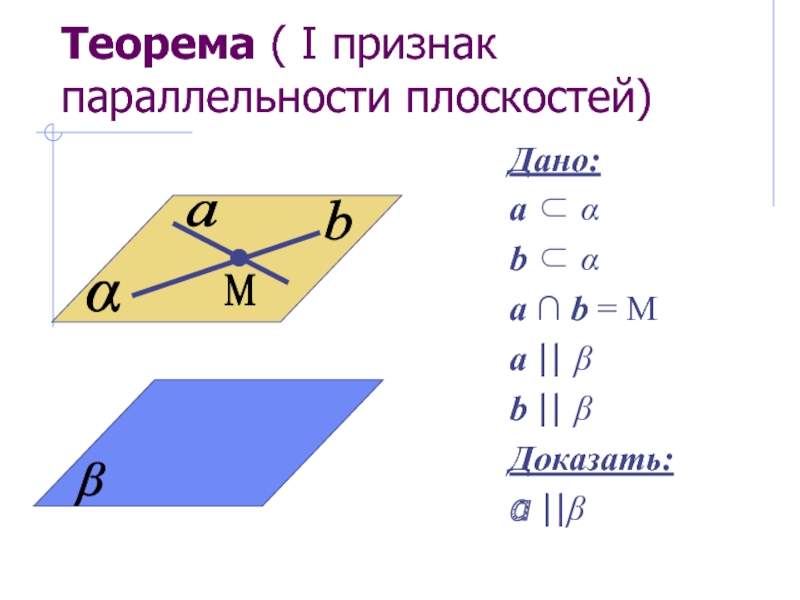
- 14. Теорема ( I признак параллельности плоскостей)Если каждая
- 15. Теорема ( I признак параллельности плоскостей)Дано:a
- 16. Идея:Рассуждаем методом от противногоПусть ∩ β = c,т.е. c и c β.
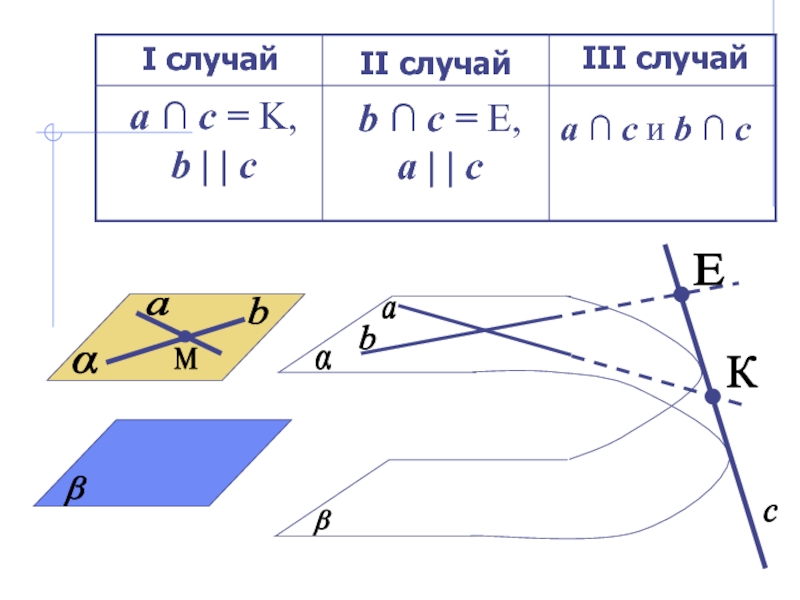
- 17. αβаbсЕКI случайII случайIII случайa ∩ c =
- 18. Пусть ∩ β = c,
- 19. Вывод:Наше предположение, что ∩ β неверно, следовательно, ||β.Теорема доказана.
- 20. Теорема ( II признак параллельности плоскостей)Если две
- 21. Затребованная помощь I карточка: условие и заключения
- 22. I карточка: условие и заключения
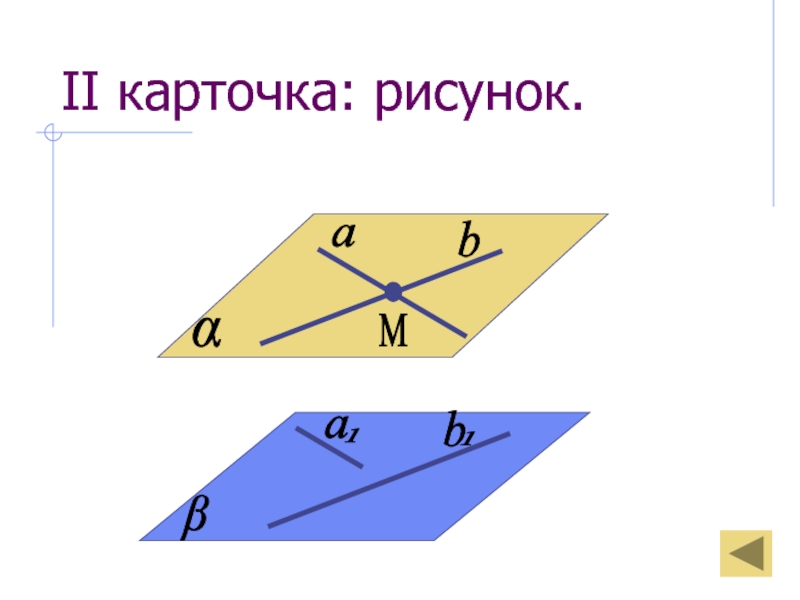
- 23. II карточка: рисунок.αβаMb
- 24. III карточка: идея доказательства.Используй предыдущую теорему I признак параллельности плоскостей
- 25. IV карточка: I этап доказательства.a ||
- 26. V карточка: II этап доказательства.Т.к. a
- 27. Идея: Использовать при доказательствеI признак параллельности плоскостей.I
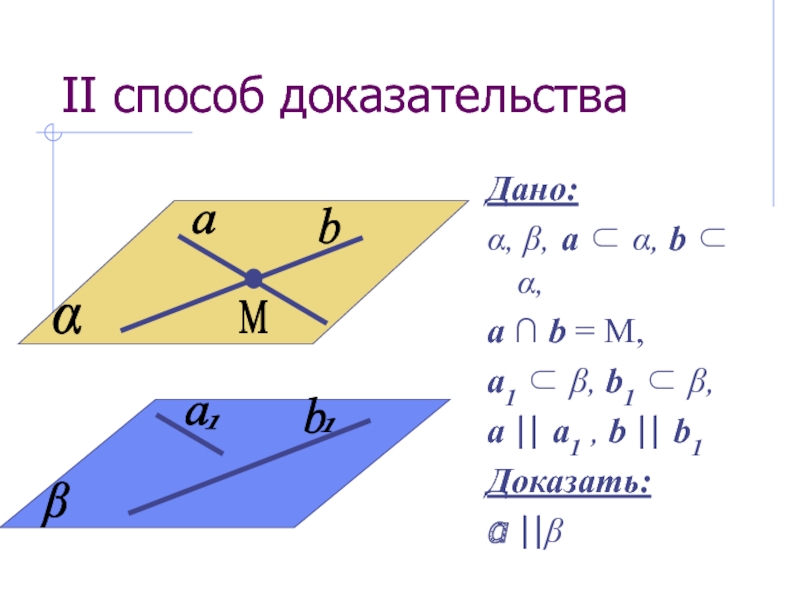
- 28. II способ доказательстваДано:, β, a ,
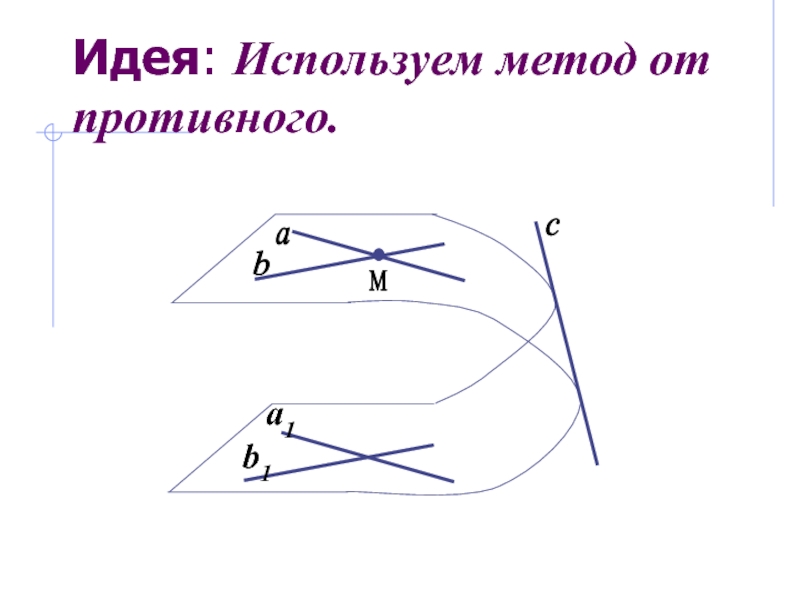
- 29. Идея: Используем метод от противного.
- 30. Доказательство:Идея: Используем метод от противного.Допустим ∩
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Это мы знаем
Прямая и плоскость в пространстве
Какие варианты расположения плоскости
и прямой мы изучили?
Слайд 7Вспомним план изучения темы
Определение
Признаки
Свойства
Задачи на построение
Применение к решению задач разного
типа
Слайд 9Две плоскости имеют общую точку, то
по аксиоме пересечения двух
плоскостей -общую прямую.
Такие плоскости называются
пресекающимися.
а
α
β
M
Слайд 12План изучения темы:
Определение параллельных плоскостей
Признаки
Свойства параллельных плоскостей
Применение при решении задач
Слайд 14Теорема ( I признак параллельности плоскостей)
Если каждая из двух пересекающихся
прямых одной плоскости параллельна другой плоскости, то данные плоскости параллельны.
Слайд 15Теорема ( I признак параллельности плоскостей)
Дано:
a
b
a
∩ b = M
a || β
b || β
Доказать:
||β
α
β
а
M
b
Слайд 18Пусть ∩ β = c, т.е. c
и c β.
a ∩ c = K, то
b ∩
c = E, тоa ∩ c и b ∩ c, то
К a ,
К β, т.к.
a ∩ β , что противоречит условию
a || β
Е b ,
Е β, т.к.
Е c и c β.
b ∩ β, что противоречит условию
b || β
К a, К β
a ∩ β
Е b, Е β
b ∩ β ,
что противоречит условию
a || β и b || β
К c и c β.
Слайд 20Теорема ( II признак параллельности плоскостей)
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости
параллельны.Докажите самостоятельно.
Слайд 21Затребованная помощь
I карточка: условие и заключения теоремы.
II карточка:
рисунок.
III карточка: идея доказательства.
IV карточка: I этап доказательства.
V карточка: II этап доказательства.Слайд 22 I карточка:
условие и заключения теоремы.
Дано:
, β, a
, b , a ∩ b = M,
a1
β, b1 β, a || a1 , b || b1
Доказать:
||β
Слайд 24 III карточка:
идея доказательства.
Используй предыдущую теорему
I признак параллельности
плоскостей
Слайд 25IV карточка:
I этап доказательства.
a || a1 , a1
β a || β (по признаку параллельности прямой и
плоскости)b || b1 , b1 β b || β (по признаку параллельности прямой и плоскости)
Слайд 26V карточка:
II этап доказательства.
Т.к. a || β и b
|| β, a ∩ b = M,
согласно I признаку
||β.
Слайд 27Идея: Использовать при доказательстве
I признак параллельности плоскостей.
I этап: доказать, что
a || β и b || β.
a || a1 ,
a1 β a || βb || b1 , b1 β b || β
(по признаку параллельности прямой и плоскости)
II этап: согласно I признаку.
a || β и b || β, a ∩ b = M, то
Вывод: ||β
Дано:
, β, a , b , a ∩ b = M,
a1 β, b1 β, a || a1 , b || b1
Доказать: ||β
Доказательство:
Слайд 28II способ доказательства
Дано:
, β, a , b ,
a ∩ b = M,
a1 β, b1 β,
a || a1 , b || b1
Доказать:
||β
Слайд 30Доказательство:
Идея: Используем метод от противного.
Допустим ∩ β = с,
т.е. с β и с
I этап:
a
|| β и b || β по признаку параллельности прямой и плоскости, то a и b не пересекают с, т.к. с β а || с и b || с, т.к. они лежат в одной плоскости.
II этап: получили противоречие с аксиомой параллельных: через точку М можно провести только одну прямую, параллельную данной прямой.
Вывод: предположение, что ∩ β неверно, т.е.
||β