Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки параллельности прямых
Содержание
- 1. Признаки параллельности прямых
- 2. Цель урока Вспомнить, какие прямые называются
- 3. Какие прямые называются параллельными? Посмотрим на схемуУкажите
- 4. Доказательство:Пусть при пересечении двух прямых a и
- 5. Второй признак параллельности прямыхЕсли при пересечении двух
- 6. ЗадачаΔАВС р/бВС основание ΔАВСДоказать, что α ׀׀bТак
- 7. Выполнить самостоятельно34Углы 3 и 4 односторонние ив
- 8. Подведение итогов урокаВ чем заключается первый признак
- 9. Математическое доминоL1 и L4L2 и L5L1 и L2L3 и L2L4 и L3
- 10. Домашнее заданиеРабочая тетрадь № 88, 89,90,91
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Признаки параллельности прямых
Открытый урок по геометрии в 7 классе, учителя
математики ГБОУ школы №212 Одабашян Марианны Степановны
Слайд 2Цель урока
Вспомнить, какие прямые называются параллельными.
Какие
пары углов образуют две прямые пересеченные
третьей секущейИзучить признаки параллельности прямых
Слайд 3Какие прямые называются параллельными?
Посмотрим на схему
Укажите накрест лежащие углы
и вспомните свойство этих углов:
Укажите односторонние углы и вспомните их
свойство:Укажите соответственные углы и вспомните свойство этих углов:
:
1
2
3
4
5
6
7
8
Две прямые на плоскости называются параллельными, если они не пересекаются
Слайд 4Доказательство:
Пусть при пересечении двух прямых a и b секущей f
накрест лежащие углы равны:
Точка О является серединой отрезка АВ, проведем
из этой точки перпендикуляр ОН к прямой а. На прямой b от точки В отложим отрезок ВН1, равный отрезку АН.Треугольник ОНА и ОН1В равны по двум сторонам и углу между ними (АО=ОВ, АН=ВН1, и ), следовательно
Из равенства углов 3 и 4 следует, что точка Н1 лежит на продолжении прямой ОН. А из равенства углов 5 и 6 следует, что ∟6 – прямой (т.к. ∟5-прямой).
Таким образом прямые a и b перпендикулярны прямой НН1, поэтому параллельны.
Для доказательства параллельности прямых необходимо знать 3 признака:
Первый признак параллельности прямых
Если при пересечении двух прямых секущей накрест лежащие углы равны. То эти прямые параллельны
a
b
f
О
Н
Н1
В
А
1
2
3
4
5
6
Слайд 5Второй признак параллельности прямых
Если при пересечении двух прямых секущей соответственные
углы равны. То эти прямые параллельны.
Доказательство:
Пусть при пересечении двух прямых
a и b секущей f соответственные углы равны:Так как углы 2 и 3 вертикальные, то они равны ∟2=∟3, то ∟1 =∟2= ∟3, а ∟1= ∟3 накрест лежащие, Следовательно прямые a и b параллельны
Третий признак параллельности прямых
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то эти прямые параллельны.
Доказательство:
Пусть при пересечении двух прямых a и b секущей f сумма односторонних углов ∟1+∟4=1800. Так как ∟3 и ∟4 смежные, то ∟3+∟4= 1800, из этих равенств следует, накрест лежащие углы 1 и 3 равны:∟1=∟3, а рас накрест лежащие углы равны, то прямые a и b параллельны.
a
b
f
1
2
3
4
Слайд 6
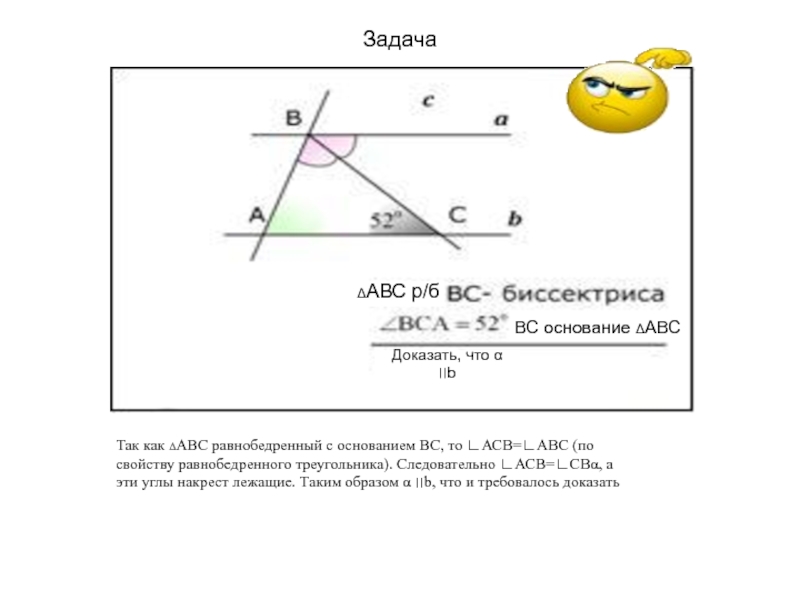
Задача
ΔАВС р/б
ВС основание ΔАВС
Доказать, что α ׀׀b
Так как ΔАВС равнобедренный
с основанием ВС, то ∟АСВ=∟АВС (по свойству равнобедренного треугольника). Следовательно
∟АСВ=∟СВα, а эти углы накрест лежащие. Таким образом α ׀׀b, что и требовалось доказатьСлайд 7Выполнить самостоятельно
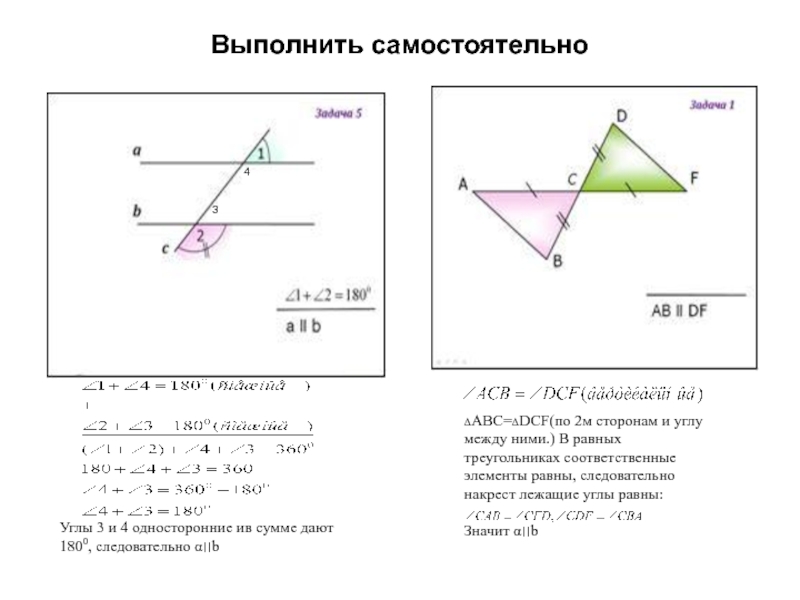
3
4
Углы 3 и 4 односторонние ив сумме дают 1800,
следовательно α׀׀b
ΔАВС=ΔDCF(по 2м сторонам и углу между ними.) В равных
треугольниках соответственные элементы равны, следовательно накрест лежащие углы равны:Значит α׀׀b