Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
проект "Логарифмическая функция"
Содержание
- 1. проект "Логарифмическая функция"
- 2. СодержаниеВведениеЦели и задачиИстория возникновенияПонятие логарифмической функции и
- 3. ВведениеНа уроках алгебры в 11 классе мы
- 4. Цели и задачиЦель: Подробно изучить логарифмическую функцию.
- 5. История возникновения В XVI в. резко возрос
- 6. Джон Непер
- 7. Йост Бюрги
- 8. Первые таблицы десятичных логарифмов (1617 г.) были
- 9. Логарифмическая линейкаЧерез 10 лет после появления
- 10. Понятие логарифмической функции, ее свойства и график
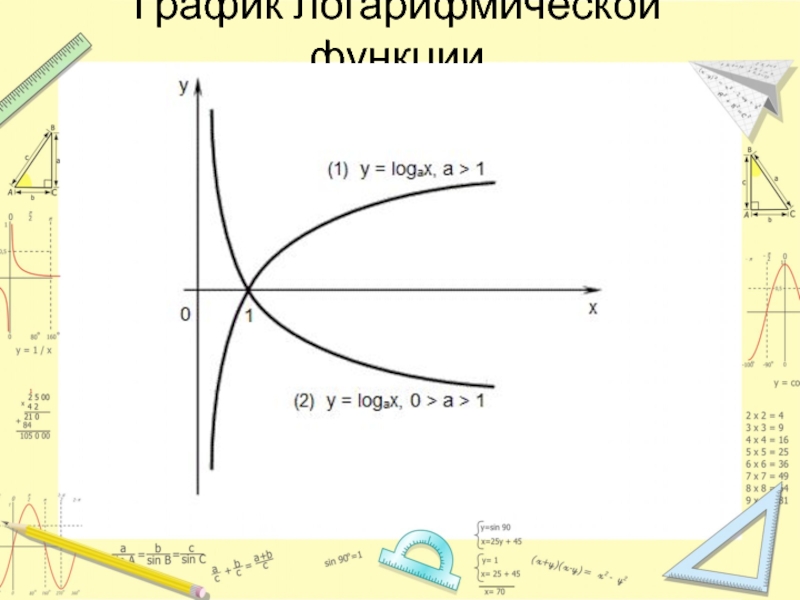
- 11. График логарифмической функции
- 12. СвойстваОбласть определения (0; +∞) Область значений: у
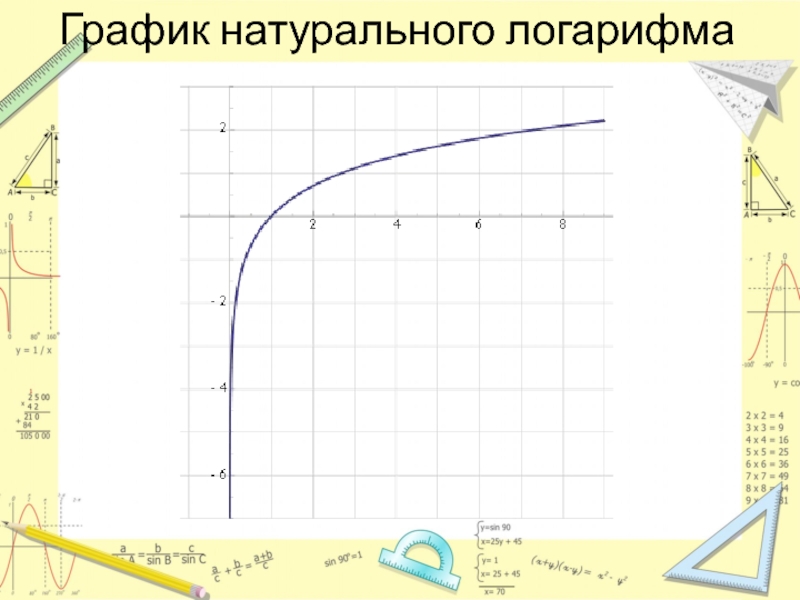
- 13. Натуральный логарифмНатуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная
- 14. График натурального логарифма
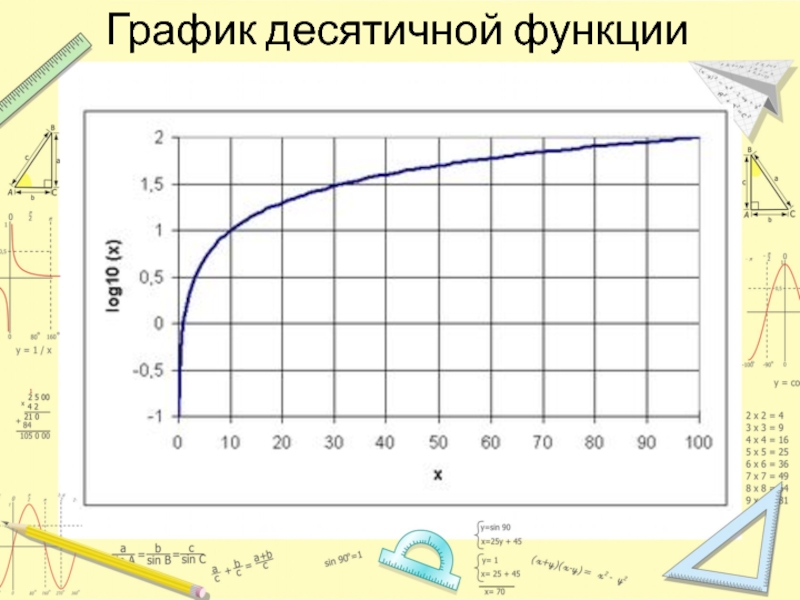
- 15. Десятичный логарифм Десятичный логарифм — логарифм по основанию 10.
- 16. График десятичной функции
- 17. Логарифмическая спиральСпираль называется логарифмической, таккак её уравнение
- 18. В математике логарифмическая спираль впервые упоминается в
- 19. Логарифмы в жизниПсихология и физиологияЧеловеческое восприятие многих явлений хорошо
- 20. Логарифмы в жизниТеория музыкиЧтобы решить вопрос о
- 21. Логарифмы в жизниБиология Ряд биологических форм хорошо
- 22. Рога архаров (горных козлов) закручены по логарифмической
- 23. АстрономияГалактики тоже кружат по спирали. Яркость звёзд
- 24. Логарифмы в ЕГЭ (примеры заданий) В5, В7, С3
- 25. ЗаключениеВ данной работе была подробно изучена логарифмическая
- 26. Применение исследовательского проектаЛогарифмическая функция крайне важна в
- 27. Скачать презентанцию
СодержаниеВведениеЦели и задачиИстория возникновенияПонятие логарифмической функции и ее графикНатуральный логарифмДесятичный логарифмЛогарифмическая спиральЛогарифмы в жизниЛогарифмы в Едином Государственном ЭкзаменеВыводЗаключениеСписок используемой литературы
Слайды и текст этой презентации
Слайд 1
Проект на тему :
«Логарифмическая функция»
Подготовили: ученики 11 «А» класса
Кашлева Татьяна,
Попова Валерия
Слайд 2Содержание
Введение
Цели и задачи
История возникновения
Понятие логарифмической функции и ее график
Натуральный логарифм
Десятичный
логарифм
Логарифмическая спираль
Логарифмы в жизни
Логарифмы в Едином Государственном Экзамене
Вывод
Заключение
Список используемой литературы
Слайд 3Введение
На уроках алгебры в 11 классе мы впервые столкнулись с
понятием логарифмической функции. Так как эта тема для нас новая
и неизведанная, мы решили исследовать ее подробнее. К тому же в заданиях ЕГЭ по математике часто встречаются задания с логарифмами. Перед нами встали вопросы: кто изобрел логарифмы? когда? Встречаются ли в повседневной жизни логарифмы?Слайд 4Цели и задачи
Цель: Подробно изучить логарифмическую функцию.
Задачи:
Изучить литературу,
интернет ресурсы.
Закрепить знания о логарифмической функции.
Оформить презентацию для защиты работы.
Слайд 5История возникновения
В XVI в. резко возрос объем работы, связанный
с вычислениями. Поэтому открытие логарифмов, сводящее умножение и деление чисел
к сложению и вычитанию их логарифмов, необычайно быстро вошли в практику.Первые таблицы логарифмов составлены
независимо друг от друга шотландским
математиком Дж. Непером (1550—1617) и
швейцарцем И. Бюрги (1552—1632).
Слайд 8Первые таблицы десятичных логарифмов (1617 г.) были составлены по совету
Непера английским математиком Г. Бриггсом (1561 —1630). Многие из них
были найдены с помощью выведенной Бриггсом приближенной формулы:Слайд 9Логарифмическая линейка
Через 10 лет после появления
логарифмических таблиц
английский математик Д .Гунтер
изобрел логарифмическую линейку.
Затем логарифмическую
линейку вытеснили калькуляторы.Но без логарифмической линейки не были бы построены ни первые компьютеры , ни калькуляторы.
Слайд 10Понятие логарифмической функции, ее свойства и график
Логарифм - определяется
как показатель степени, в которую надо возвести основание a, чтобы
получить число b.logab=x, ax=b
Слайд 12Свойства
Область определения (0; +∞)
Область значений: у R
Чётность /нечётность:
функция не является ни четной, ни
Нечетной
Нули функции: y =
0 при x = 1Промежутки знакопостоянства: если 0 < a < 1, то y > 0 при
x (0; 1), y < 0 при x (1; ) если a > 1, то y > 0 при x (1; ), y
< 0 при x (0; 1)
Монотонность:
при 0 < a < 1 функция убывает при x (0; +∞ );
при a > 1 функция возрастает при x (0; +∞ )
Экстремумов нет.
График функции проходит через точку: (1; 0)
Асимптота x = 0
Слайд 13Натуральный логарифм
Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный
логарифм обычно обозначают как ln(x), loge(x).
Натуральный логарифм числа x (записывается как ln(x)) —
это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389...) равен 2, потому что e2=7,389.... Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e0 = 1.Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный».
Слайд 15Десятичный логарифм
Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный
логарифм числа есть решение уравнения 10x=b
Десятичный логарифм числа b существует, если b>0. Принято
обозначать его lg b. Примеры:lg 1 = 0; lg 10 = 1 lg 0, = --1
Слайд 17Логарифмическая спираль
Спираль называется логарифмической, так
как её уравнение связано с
Логарифмической функцией.
Вращение
ножей в
механизмах, изгиб трубы
турбины – примеры того,
где
встречается логарифмическая спираль.
Слайд 18В математике
логарифмическая спираль
впервые упоминается в
1638 году Рене
Декартом.
Якоб Бернулли открыл
Поразительное свойство
спирали: кривая с
«твёрдым» характером.
Она
не изменяется при сжатиях, растяжениях
и поворотах .
Слайд 19Логарифмы в жизни
Психология и физиология
Человеческое восприятие многих явлений хорошо описывается логарифмическим законом.
Закон
Вебера — Фехнера — эмпирический психофизиологический закон, заключающийся в том, что интенсивность ощущения пропорциональна логарифму
интенсивности стимула — громкости звука, яркости света.Закон Фиттса: чем дальше или точнее выполняется движение организма, тем больше коррекции необходимо для его выполнения и тем дольше эта коррекция исполняется.
Время на принятие решения при наличии выбора можно оценить по закону Хикса.
Слайд 20Логарифмы в жизни
Теория музыки
Чтобы решить вопрос о том, на сколько
частей делить октаву, требуется отыскать рациональное приближение
для
. Если разложить это число в непрерывную дробь, то третья подходящая дробь (7/12) позволяет обосновать классическое деление октавы на 12 полутонов.Вредное влияние промышленных шумов на здоровье рабочих побудило выработать приёмы точной числовой оценки громкости звука «бел».
Громкость, выраженная в белах, равна десятичному логарифму величины раздражения .
Слайд 21Логарифмы в жизни
Биология
Ряд биологических форм хорошо соответствует логарифмической спирали — кривой,
у которой касательная в каждой точке образует с радиус-вектором в
этой точке один и тот же угол, то есть прирост радиуса на единицу длины окружности постоянен:Раковина наутилуса
Слайд 22Рога архаров (горных козлов) закручены по логарифмической спирали. И можно
сказать, что эта спираль является математическим символом в соотношении форм
роста.Слайд 23Астрономия
Галактики тоже кружат
по спирали.
Яркость звёзд оценивают
по логарифмической
шкале с основанием 2,5.
А величина звезды
представляет собой
логарифм её
яркостиСлайд 25Заключение
В данной работе была подробно изучена логарифмическая функция. Изучена литература
и интернет ресурсы. Знания о логарифмической функции закреплены с помощью
решения заданий.Слайд 26Применение исследовательского проекта
Логарифмическая функция крайне важна в экономике, физике, при
проведении научных, экспериментальных расчетов, астрономии и др. Форма логарифмической спирали
присуща многим природным объектам.Физика — интенсивность звука (децибелы).
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.