Простые числа

работы
Теоретическая часть: исторические сведения; свойства простых чисел
Практическая часть: нахождение простых

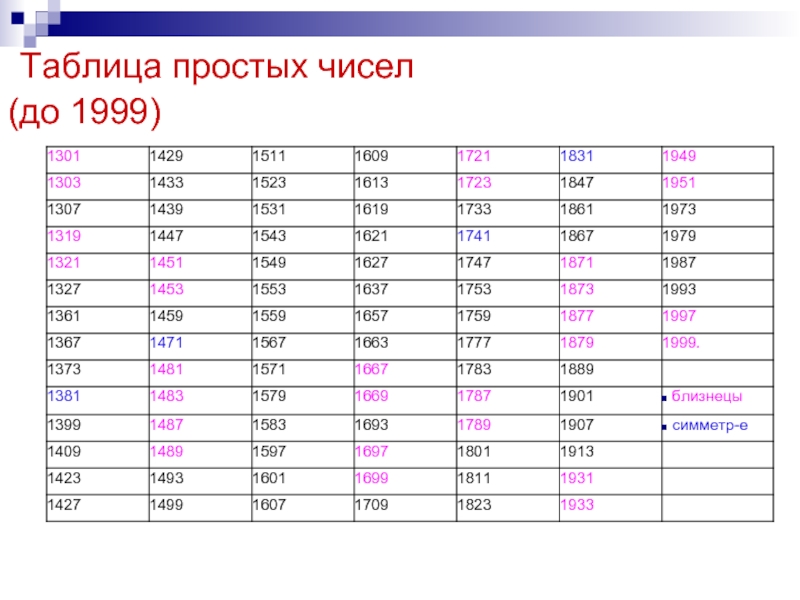
чисел, путем освоения метода «Решето Эратосфена»; составление таблицы
Заключение
Использованная литература

два делителя: единицу и само это число. Например: 3 –

простое число. Оно нацело делится на 1 и на само себя, т.е. на 3.
Если число имеет более двух делителей, то называется составным.

тему «Простые и составные числа», и меня настолько заинтересовала это

тема, что я написала в прошлом году краткую исследовательскую работу на тему «Простые числа». В этом году продолжила свое исследование.

некоторых свойств и нахождение простых чисел через освоение метода «Решето

Эратосфена».

собрать и изучить материал.
2. открыть какие-либо закономерности и свойства

в ряду чисел.
3. найти простые числа больше числа 997 методом «Решето Эратосфена».

2000 лет до н.э., составил первую таблицу простых чисел, которая

получила название «Решето Эратосфена».

А почему решето? Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето.

воском, и последовательно прокалывал составные числа. Таким образом, на доске

нетронутыми остались лишь простые числа, а составные числа исчезали, как бы просеивались. Оставив нетронутым число 2, он далее прокалывал числа 4,6,8…, т.е. все четные числа, кратные двум. Следующее простое число 3, а все числа, кратные трем, уже составные, поэтому прокалывались все числа через два в третье. Оставив число 5 как простое, прокалываются все числа, кратные 5, т.е. каждое пятое число, и т.д.

В своей книге «Начала», бывшей на протяжении двух тысяч лет

основным учебником математики, доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть ещё большее простое число.

Но предел простого числа не сумеем найти, т.к. они бесконечны

как 5 и 7, 11 и 13, 17 и 19

и т.д. получили образное название «близнецы».
Три числа, которые отличаются на 2, называются «тройняшками», 3, 5, 7.
Мы эти числа можем посмотреть в учебнике математики 6 класса

них 16 чисел – палиндромические – каждое равно обращённому Например:

11,101, 131, 151, 181, 191, 313, 353, и т.д.
симметричные себе простые числа: 107 – 701, 113 – 311, 149 – 941 и т.д.,
простые числа могут разместиться в магическом квадрате

числа вида Мр=2р-1. М2=22-1=3 т.е. М2=3, М3=7, М5=31, М7=127

Любое четное число, больше 2, можно представить в виде суммы 2-х простых чисел. Например: 4=2+2, 6=3+3, 8=5+3, 10=3+7, 12=5+7, 14=7+7, 16=11+5, 18=7+11, 20=3+17 и т.д. Но это утверждение не доказано. Такую задачу называют проблемой Варинга

суммы трех простых чисел.
Например: 7=2+3+2, 9=2+5+2, 11=5+3+3, 13=5+5+3,

15=7+5+3, 17=5+5+7, 19=5+7+7, 21=3+7+11, 23=5+7+11, 25=17+3+5 и т.д.

и составление таблицы

Отсюда сформулировала гипотезу, что указать самое большое простое число невозможно,

т.к. они бесконечны. Эту теорему доказал древнегреческий математик Евклид III в. до н.э.
В ходе работы были найдены 92 простые числа методом «Решето Эратосфена».

«Мнемозида», Москва 2007
Школьная энциклопедия «Математика. Том 11». Издательство «Аванта+»., М.

2003
Энциклопедия для детей «История Древнего мира». Издательство «Олимо-пресс Образования»., М 2003
Предметная неделя истории в школе. Составители: И.И. Варакина, С.В. Парецкова. Издательство «Корифей», Волгоград
Шамаев Иван Иванович «Учись открывать новое». Издательство «Бичик»., Якутск: 1999г
диск «Портфолио 3» Занятные стайки простых чисел