Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольный треугольник. Теорема Пифагора.
Содержание
- 1. Прямоугольный треугольник. Теорема Пифагора.
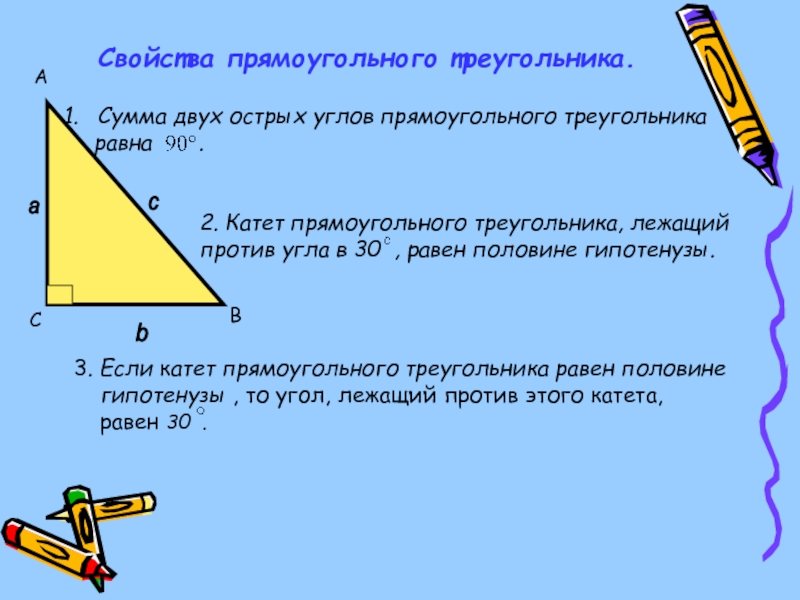
- 2. Свойства прямоугольного треугольника.
- 3. Синус, косинус и тангенс острого угла прямоугольного
- 4. Великий ученый Пифагор родился около 570 г.
- 5. Интересна история теоремы Пифагора. Хотя эта теорема
- 6. Теорема Пифагора.В прямоугольном треугольнике квадрат гипотенузы равен
- 7. доказательство(1):Пусть АВС — данный прямоугольный треугольник с
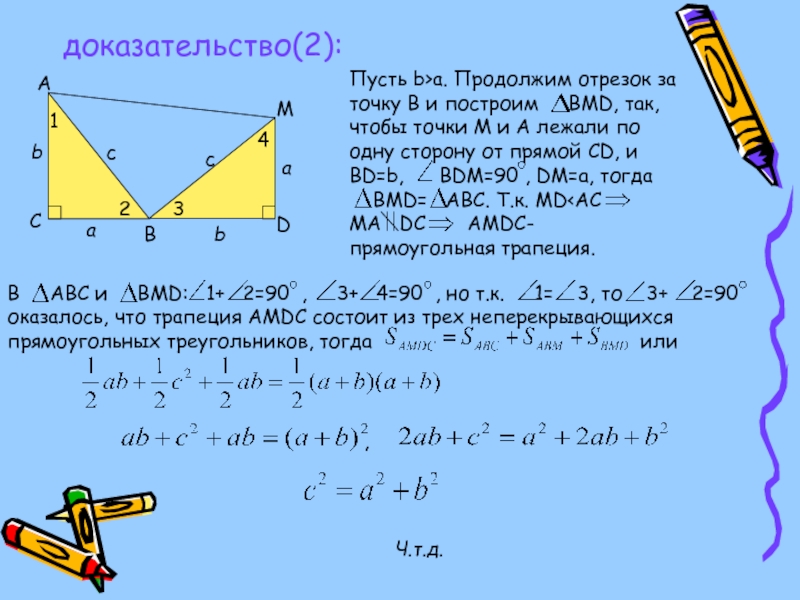
- 8. доказательство(2):Ч.т.д.
- 9. Формулировка теоремы, обратной теореме ПифагораЕсли квадрат одной
- 10. Пифагоровы тройки.Можно доказать, что катеты a, b
- 11. Египетский треугольникТреугольник со сторонами 3, 4, 5
- 12. Тополь у реки«На береге реки рос тополь
- 13. Задача 1.Решение:
- 14. Задача 2.
- 15. Задача 3.Лестницу длиной 6 м, упирающуюся одним
- 16. Домашнее задание:Возьмите лист бумаги в виде прямоугольника
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Прямоугольный треугольник. Теорема Пифагора.
Урок геометрии
8 класс
Учитель математики Будзинская
М.Ф.
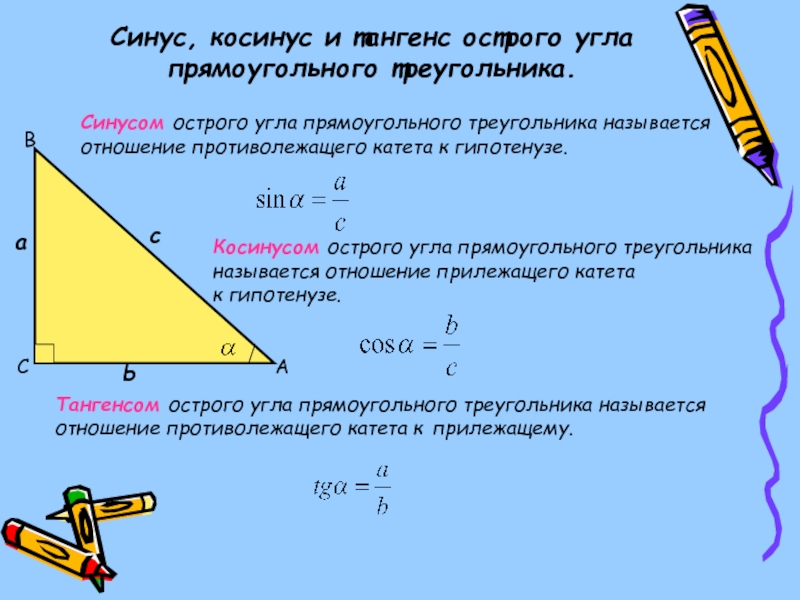
Слайд 3Синус, косинус и тангенс острого угла прямоугольного треугольника.
Синусом острого
угла прямоугольного треугольника называется
отношение противолежащего катета к гипотенузе.
Косинусом острого угла
прямоугольного треугольника называется отношение прилежащего катета
к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется
отношение противолежащего катета к прилежащему.
Слайд 4
Великий ученый Пифагор родился около 570 г. до н.э. на
острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Имя же матери Пифагора не известно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского.Пифагор
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принципов достойны подражания и сейчас.
Слайд 5Интересна история теоремы Пифагора. Хотя эта теорема и связывается
с
именем Пифагора, она была известна задолго до него. В вавилонских
текстах
она встречается за 1200 лет до Пифагора. По-видимому, он первымнашёл её доказательство. Сохранилось древнее предание, что в честь своего
открытия Пифагор принёс в жертву богам быка, по другим свидетельствам –
даже сто быков. Это, однако, противоречит сведениям о моральных и
Религиозных воззрениях Пифагора. В литературных источниках можно
прочитать, что он "запрещал даже убивать животных, а тем более ими
кормиться, ибо животные имеют душу, как и мы". В связи с этим более
правдоподобной можно считать следующую запись:
"… когда он открыл, что в прямоугольном треугольнике
гипотенуза имеет соответствие с катетами, он принес в жертву быка,
сделанного из пшеничного теста".
На протяжении последующих веков были найдены другие доказательства
теоремы Пифагора. В настоящее время их насчитывается более ста.
История теоремы Пифагора.
Слайд 6Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 7доказательство(1):
Пусть АВС — данный прямоугольный треугольник с прямым углом С.
Проведем
высоту CD из вершины прямого угла С .
Теорема доказана.
Слайд 9Формулировка теоремы, обратной теореме Пифагора
Если квадрат одной стороны треугольника
равен
сумме квадратов двух других сторон,
то треугольник прямоугольный.
Слайд 10Пифагоровы тройки.
Можно доказать, что катеты a, b и гипотенуза с
таких треугольников выражаются формулами
Где m и n- любые натуральные
числа, такие, что m>n.Слайд 11Египетский треугольник
Треугольник со сторонами 3, 4, 5 часто называют египетским
треугольником, т.к. он был известен еще древним египтянам.
Для построения прямых
углов египтяне поступали так: на веревке делали метки, делящие ее на 12 равных частей, связывали ее концы и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами 3 и 4 оказывался прямым.Слайд 12Тополь у реки
«На береге реки рос тополь одинокий.
Вдруг ветра порыв
его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки
его угол составлял.Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Слайд 15Задача 3.
Лестницу длиной 6 м, упирающуюся одним концом в стену,
а другой конец которой отстоит от стены на 3 м,
подвинули к стене на 1 м. На сколько ее верхний конец стал выше?1
Решение:
Слайд 16Домашнее задание:
Возьмите лист бумаги в виде прямоугольника и согните его
так, чтобы одна из вершин листа оказалась в середине стороны,
не содержащей ее.Как вычислить длину линии сгиба, сделав как можно меньше измерений?
2. В прямоугольном треугольнике рассмотрим такие величины:
оба катета, гипотенузу, медианы ко всем сторонам. Выберите
две из них, и считая их известными, укажите план
нахождения остальных.