Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные виды уравнения прямой
Содержание
- 1. Различные виды уравнения прямой
- 2. Общее уравнение прямойУравнение Ax+By+C=0 (где A, B
- 3. Ах+Ву+С=01) Если A=0, то уравнение представляет прямую,
- 4. Ах+Ву+С=02) Если В=0, то уравнение представляет прямую,
- 5. Ах+Ву+С=03) Когда В=0, то у=Уравнение у=кх+m, где
- 6. Ах+Ву+С=0(у=
- 7. Пример 3.Составить уравнение прямой, изображенной на рисунке.
- 8. Пример 4.Составить уравнение прямой, изображенной на рисунке.Решение.Данная
- 9. Теоремы Уравнение изображенной прямой
- 10. Теорема 2. Уравнение
- 11. Вывод уравнения прямой в отрезках.
- 12. у=кх+m Для этого перенесем
- 13. Рассмотрим следующий пример Пример 5.
- 14. Пример 5. 2)
- 15. Уравнение прямой, проходящей через две точки.
- 16. Решим эту задачу в общем виде.
- 17. Решим эту задачу в общем виде.
- 18. Преобразуем его у-у1=
- 19. (у-у1) (х2-х1)=(у2-у1) (х-х1) А
- 20. В первом случае
- 21. Пример 6. Записать уравнение прямой,
- 22. Рассмотрим задачу: «Лежат ли
- 23. Итак: «Лежат ли точки А1 (-2;5), А2
- 24. Спасибо за внимание!!!
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Различные виды уравнения прямой
презентацию подготовила
ученица 7 «Б» класса
МОУ «Гимназия №1»
Распарина
Ольга
Слайд 2Общее уравнение прямой
Уравнение Ax+By+C=0 (где A, B и C могут
принимать любые значения, лишь бы коэффициенты A, B не были
равны нулю оба сразу) представляет прямую линию.Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.
Слайд 3Ах+Ву+С=0
1) Если A=0, то уравнение представляет прямую, параллельную оси Ох
(у= ).
Пример 1.
Графиком уравнения у=-10 является прямая, параллельная
оси Ох и проходящая через точку (0;-10). Слайд 4Ах+Ву+С=0
2) Если В=0, то уравнение представляет прямую, параллельную оси Оу
(х= ).
Пример 2.
Графиком уравнения х=6 является прямая, параллельная оси
Оу и проходящая через точку (6;0).
Слайд 5Ах+Ву+С=0
3) Когда В=0, то у=
Уравнение у=кх+m, где к=
, а m= называется уравнением прямой с угловым коэффициентом
к.4) Если С=0, то есть уравнение Ах+Ву+С=0 не содержит свободного члена, то оно представляет прямую, проходящую через начало координат.
Слайд 6Ах+Ву+С=0
(у= ,
то есть у=кх – где к – угловой коэффициент прямой.
Ясно, что к= , где Х0 и У0 координаты произвольной точки прямой, Х0=0).х
у
у0
х0
1
0
1
Слайд 7Пример 3.
Составить уравнение прямой, изображенной на рисунке.
Решение.
Так как прямая проходит через начало координат, то она задается уравнением у=кх. Определим угловой коэффициент этой прямой. Возьмем к примеру точку А этой прямой, тогда к= , то есть к= . Значит, к=-2 и уравнение данной прямой имеет вид: у=-2х.
0
у
х
-1
1
1
-1
А
2
Слайд 8Пример 4.
Составить уравнение прямой, изображенной на рисунке.
Решение.
Данная прямая получена из
прямой у=кх смещением последней на 3 ед. отрезка вверх вдоль
оси Оу. Прямые у=кх и данная параллельны, следовательно, их угловые коэффициенты равны. Определив угловой коэффициент прямой у=кх (к= ), получим, что угловой коэффициент данной прямой равен -2. А так как данная прямая пересекает ось Оу в точке с ординатой 3, то в уравнении данной прямой (у=кх+m), к=-2, m=3. Искомое уравнение имеет вид у= =-2х+3.у=кх
у
х
А
Слайд 9Теоремы
Уравнение изображенной прямой можно получить и
иначе, если иметь ввиду следующие утверждения.
Теорема 1.
Если прямая отсекает на осях отрезки а и в (не равные нулю), то ее можно представить уравнением =1.Слайд 10Теорема 2.
Уравнение =1 представляет
прямую, отсекающую на осях (считая от начала координат) отрезки а
и в.Уравнение =1 называется уравнением прямой в отрезках (ясно, что а=0, в=0).
Слайд 11Вывод уравнения прямой в отрезках.
Уравнение прямой в
отрезках легко получается либо из общего уравнения прямой, либо из
уравнения прямой с угловым коэффициентом.Пусть у=кх+m – уравнение прямой с угловым коэффициентом. Приведем его к виду =1.
Слайд 12у=кх+m
Для этого перенесем слагаемое кх в
левую часть уравнения, изменив его знак на противоположный и разделим
обе части полученного равенства на m. Получим следующее уравнение =1. Перепишем это уравнение в виде =1.Учтем, что = . Следовательно, = . Обозначив буквой «а», а m – буквой «в» получим искомое уравнение прямой в отрезках =1.
Слайд 13Рассмотрим следующий пример
Пример 5.
Составить
уравнение прямой, изображенной на рисунке.
Решение.
Прямая
отсекает отрезки -2 на оси Оу и 3 – на оси Ох. Поэтому ее уравнение можно записать так:1) =1 или =1. Из последнего уравнения можно получить уравнение прямой в общем виде и уравнение прямой с угловым коэффициентом. у
Слайд 14Пример 5.
2) =1 6.
2х-3у=6. 2х-3у-6=0.
3) =1. = 1 2. у= -2.В ответе можно записать любое из уравнений 1), 2) или 3).
Кроме того, уравнение прямой в отрезках удобно использовать для построения этой прямой на чертеже.
Слайд 15Уравнение прямой, проходящей через две точки.
Теперь, допустим,
нужно записать уравнение прямой проходящей через две точки А (1;-2)
и В (-1;4). Очевидно, что для решения этой задачи надо составить и решить систему уравненийотносительно к и m, где х1=1, у1=-2,
х2=-1, у2=4. И, найдя значения к и m, подставить их в уравнение у=кх+m. Всякий раз решать подобные задачи таким способом довольно-таки нерационально.
у2=кх2+m.
у1=кх1+m,
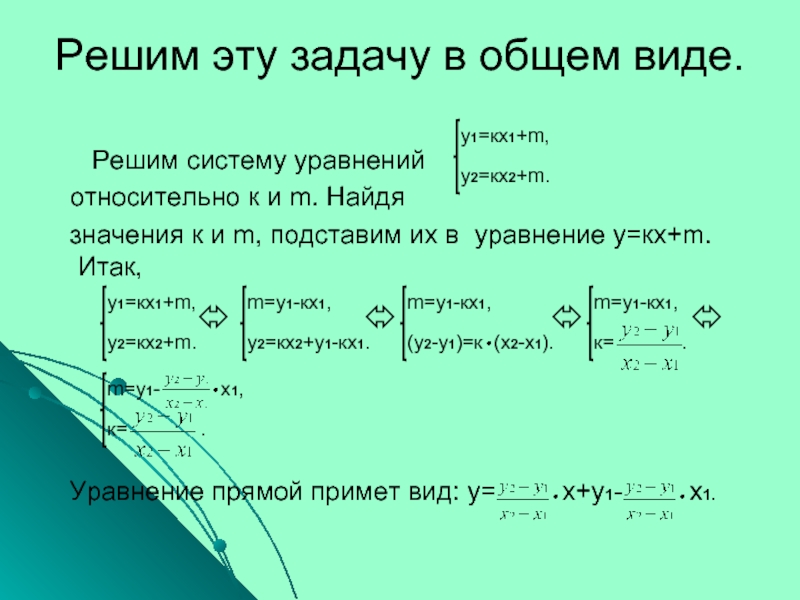
Слайд 16Решим эту задачу в общем виде.
Пусть
требуется составить уравнение прямой, проходящей через две различные точки (х1;у1)
и (х2;у2) такие, что х1=х2, у1=у2.Так как прямая проходит через эти точки, то их координаты удовлетворяют уравнению прямой у=кх+m.
Слайд 17Решим эту задачу в общем виде.
Решим систему
уравнений
относительно к и m. Найдя
значения к и m, подставим их в уравнение у=кх+m. Итак, Уравнение прямой примет вид: у= х+у1- х1.
у2=кх2+m.
у1=кх1+m,
m=у1-кх1,
у2=кх2+у1-кх1.
m=у1-кх1,
у2=кх2+m.
у1=кх1+m,
к= .
(у2-у1)=к (х2-х1).
m=у1-кх1,
m=у1- х1,
к= .
Слайд 18Преобразуем его
у-у1= х-
х1,
у-у1=
(х-х1). (у-у1) (х2-х1)=(у2-у1) (х-х1) (х2-х1) (у2-у1),
Мы получили уравнение прямой, проходящей через две различные точки (х1;у1) и (х2;у2), причем х1=х2, у1=у2.
,
,
Слайд 19(у-у1) (х2-х1)=(у2-у1) (х-х1)
А что если х2=х1
(при условии, что у2=у1) или у2=у1 (при условии, что х2=х1)?
В этом случае уравнение ( ) будет выглядеть так:
(у2-у1) (х-х1)=0 или (у-у1) (х2-х1)=0. Откуда получим уравнения: х=х1 или у=у1. То есть уравнения прямых, параллельных координатным осям.
Слайд 20 В первом случае – уравнение прямой,
параллельной оси Оу, а во втором случае – уравнение прямой,
параллельной оси Ох.у
х
Слайд 21Пример 6.
Записать уравнение прямой, проходящей через точки
А (1;-2) и В (-1;4).
Решение.
Воспользуемся уравнением
прямой, проходящей через две различные точки. Перепишем его в виде
Теперь подставим в него координаты данных точек:
Итак, у=-3х+1 – уравнение прямой, проходящей через точки А(1;-2) и В (-1;4).
Ответ: у=-3х+1
(-6)
-3(х-1)=у+2.
у=-3х+1.
Слайд 22Рассмотрим задачу:
«Лежат ли точки А1 (-2;5),
А2 (4;3), А3 (16;-1) на одной прямой?».
Решить ее можно так:1) Составить уравнение прямой, проходящей, например, через точки А1 и А2.
2) Подставить координаты точки А3 в полученное уравнение, проверив тем самым, принадлежит ли точка А3 прямой, проходящей через точки А1 и А2.
Слайд 23Итак: «Лежат ли точки А1 (-2;5), А2 (4;3), А3 (16;-1)
на одной прямой?»
Использование уравнения прямой, проходящей через
две различные точки, значительно сокращает процесс поиска решения данной задачи. Положив в уравнении х=х3, у=у3 и, подставив координаты данных точек в равенство ,получим: . Полученное равенство верное, следовательно, точки А1, А2 и А3 лежат на одной прямой .
Итак, использование различных видов уравнений прямой позволяет рационализировать поиск решения ряда задач.