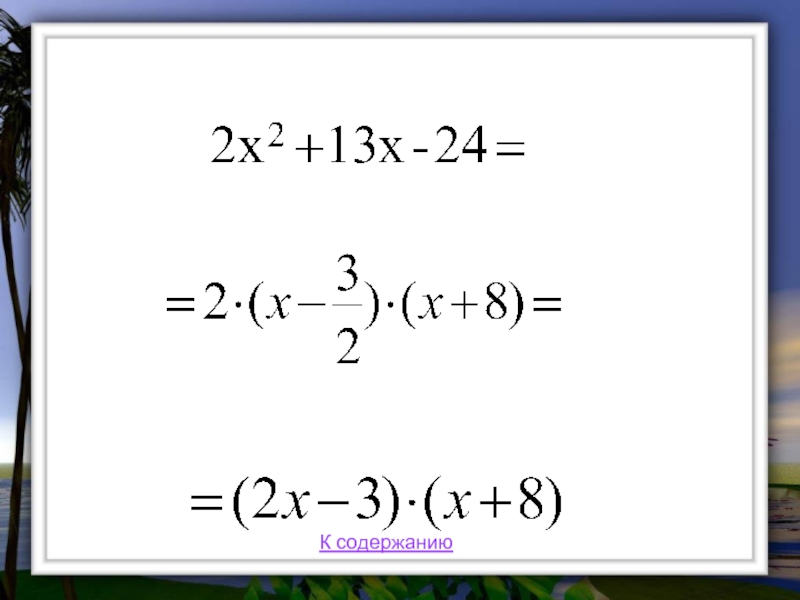Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разложение многочлена на множители с помощью комбинации различных приемов
Содержание
- 1. Разложение многочлена на множители с помощью комбинации различных приемов
- 2. СодержаниеФормулы сокращенного умноженияВынесение общего множителя за скобкиСпособ группировкиРазложение квадратного трехчлена на множителиК содержанию
- 3. Формулы сокращенного умножения
- 4. 1. Квадрат суммыДоказательство:К таблицеК содержанию
- 5. 2. Квадрат разностиК таблицеК содержаниюДоказательство:
- 6. 3. Разность квадратовК таблицеК содержаниюДоказательство:
- 7. 4. Куб суммыК таблицеК содержаниюДоказательство:
- 8. 5. Куб разностиК таблицеК содержаниюДоказательство:
- 9. 6. Сумма кубовК таблицеК содержаниюДоказательство:
- 10. 7. Разность кубовК таблицеК содержаниюДоказательство:
- 11. Вынесение общего множителя
- 12. Алгоритм нахождения общего множителя нескольких одночленовНайти наибольший
- 13. Пример Разложить на множители: x4y3 -
- 14. Способ группировки Бывает, что члены
- 15. 1. Сгруппировать его члены так, чтобы
- 16. Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители многочлен xy–6+3x–2y
- 17. xy-6+3x-2y==(xy-6)+(3x-2y).Группировка неудачна.Первый способ группировки:
- 18. Второй способ группировкиxy-6+3x-2y=(xy+3x)+(-6-2y)= =x(y+3)-2(y+3)==(y+3)(x-2).
- 19. xy-6+3y-2y=(xy-2y)+(-6+3x)= =y(x-2)+3(x-2)==(x-2)(y+3). Третий способ группировки:
- 20. Как видите, не всегда с первого раза
- 21. Разложение квадратного трехчлена на множители
- 22. К содержанию
- 23. Спасибо за внимание!Богданова А.В. г. Миасс
- 24. Скачать презентанцию
СодержаниеФормулы сокращенного умноженияВынесение общего множителя за скобкиСпособ группировкиРазложение квадратного трехчлена на множителиК содержанию
Слайды и текст этой презентации
Слайд 2Содержание
Формулы сокращенного умножения
Вынесение общего множителя за скобки
Способ группировки
Разложение квадратного трехчлена
на множители
Слайд 11 Вынесение общего множителя за скобки Из каждого слагаемого, входящего в многочлен,
выносится некоторый одночлен, входящий в качестве множителя во все слагаемые. Таким
общим множителем может быть не только одночлен, но и многочлен.Слайд 12Алгоритм нахождения общего множителя нескольких одночленов
Найти наибольший общий делитель коэффициентов
всех одночленов, входящих в многочлен, - он и будет общим
числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Слайд 13Пример
Разложить на множители:
x4y3 - 2x3y2 + 5x2.
Воспользуемся сформулированным алгоритмом.
Наибольший общий
делитель коэффициентов
–1, -2 и 5 равен 1.Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2.
Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
Вывод: за скобки можно вынести x2. Правда, в данном случае целесообразнее вынести -x2. Получим:
-x4y3-2x3y2+5x2=-x2(x2y3+2xy2-5).
К содержанию
Слайд 14Способ
группировки
Бывает, что члены многочлена не имеют общего множителя, но
после заключения нескольких членов в скобки (на основе переместительного и
сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.Слайд 15
1. Сгруппировать его члены так, чтобы слагаемые в каждой
группе имели общий множитель
2. Вынести в каждой группе общий множитель
в виде одночлена за скобки3. Вынести в каждой группе общий множитель (в виде многочлена) за скобки.
Алгоритм разложения многочлена на множители способом группировки:
Слайд 16 Для уяснения сути способа группировки рассмотрим следующий пример: разложить на множители
многочлен
xy–6+3x–2y
Слайд 20Как видите, не всегда с первого раза группировка оказывается удачной.
Если группировка оказалась неудачной, откажитесь от нее, ищите иной способ.
По мере приобретения опыта вы будете быстро находить удачную группировку.xy-6+3y-2y=(x-2)(y+3).
К содержанию
Теги