Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение комбинаторных задач
Содержание
- 1. Решение комбинаторных задач
- 2. Сколько существует вариантов покупки одной розы, если
- 3. Правило суммыЕсли некоторый элемент А можно
- 4. Задача №2.В столовой есть 2 первых
- 5. Правило произведенияЕсли некоторый элемент А можно
- 6. На блюде лежат 8 яблок, 3 груши
- 7. На блюде лежат 8 яблок, 3 груши
- 8. И пакетике драже лежат 9 красных, 10
- 9. Сколько различных двузначных чисел можно составить, используя
- 10. Сколько различных двузначных чисел можно составить, используя
- 11. Сколько различных двузначных чисел можно составить, используя
- 12. Сколько различных трехзначных чисел можно составить используя
- 13. Сколько различных двузначных чисел можно составить, используя
- 14. Сколько различных трехзначных чисел можно составить, используя
- 15. Комбинаторика – это раздел математики, посвященный решению
- 16. Рождение комбинаторики как раздела математики связано с
- 17. Смыкалова Е. В. Дополнительные главы по
- 18. Титульный лист: http://www.mathpages.com/HoME/icombina.htmСлайд 2: http://pzvezda.ru/alye-rozy-pesnya.html ; http://alfadogy.ru/dizaine/1811-fotostok-cvety-rozy-krasnye-i-alye;http://mirgif.com/malenkie-animacionnye_kartinki-cvety.htm
- 19. Скачать презентанцию
Сколько существует вариантов покупки одной розы, если продают 3 алые, 2 белые и 4 желтые розы?9способов Задача №1.Правило суммыЭто важноВажно помнить, что выбирается не просто красная, белая или желтая роза, а
Слайды и текст этой презентации
Слайд 2Сколько существует вариантов покупки одной розы, если продают
3 алые,
2 белые и 4 желтые розы?
9
способов
Задача №1.
Правило суммы
Это важно
Важно
помнить, что выбирается не просто красная, белая или желтая роза, а одна конкретная роза: эта красная или эта белая, или эта желтая роза.
Слайд 3 Правило суммы
Если некоторый элемент А можно выбрать n способами,
а элемент В – m способами, то выбор «либо А,
либо В» можно сделать n + m способами. A – n способов
В – m способов
А или В – (n + m)способов
Вернуться к решению задачи №3
Слайд 4 Задача №2.
В столовой есть 2 первых блюда и 3
вторых. Сколько различных вариантов обеда из 2 блюд можно заказать?
Первое блюдо:
Второе блюдо:
3 + 3 =
Правило произведения
2 ∙ 3 = 6 способов
2
3
Слайд 5 Правило произведения
Если некоторый элемент А можно выбрать n способами,
а элемент В – m способами, то пару А и
В можно выбрать n ∙ m способами. A – n способов
В – m способов
А и В – (n ∙ m)способов
Вернуться к решению задачи №3
Слайд 6На блюде лежат 8 яблок, 3 груши и 4 апельсина.
Задача №3.
Правило суммы
а) Сколькими способами можно взять один плод?
8 +
3 + 4 = 15 способов б) Сколькими способами можно взять:
яблоко с грушей
яблоко с апельсином
грушу с апельсином
яблоко, грушу и апельсин
Правило произведения
8 · 3 = 24 способа
8 · 4 = 32 способа
3 · 4 = 12 способов
Выбирается 1 плод.
Выбирается 2 или 3 плода.
8 · 3 · 4 = 96 способов
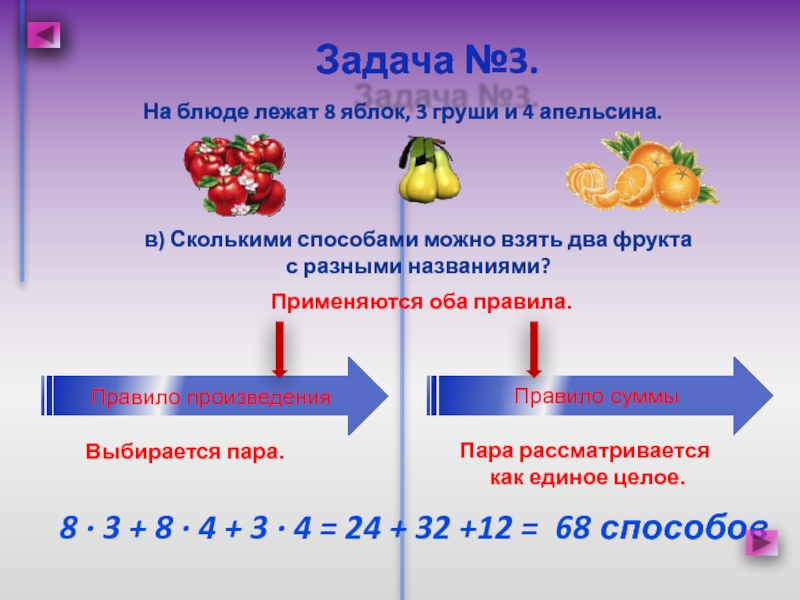
Слайд 7На блюде лежат 8 яблок, 3 груши и 4 апельсина.
Задача №3.
в) Сколькими способами можно взять два фрукта
с разными
названиями?Применяются оба правила.
Правило произведения
Правило суммы
Выбирается пара.
Пара рассматривается
как единое целое.
8 · 3 + 8 · 4 + 3 · 4 = 24 + 32 +12 = 68 способов
Слайд 8И пакетике драже лежат 9 красных, 10 синих
и 12
зеленых конфет.
Задача №4.
Самостоятельная работа.
а) Сколькими способами можно взять 1
конфету?б) Сколькими способами можно взять:
в) Сколькими способами можно взять две конфеты разного цвета?
Проверка(5)
а) 9 + 10+ 12 = 31способ
б) 9 · 10 = 90 способов
9 · 12 = 108 способов
10· 12 = 120 способов
в) 9 · 10 + 9 · 12 + 10 · 12 = 318 способов
красную и синюю конфеты
красную и зеленую конфеты
синюю и зеленую конфеты
Слайд 9Сколько различных двузначных чисел можно составить, используя цифры 1,4, и
7, если цифры могут повторяться.
Задача №5.
1 способ (перебор)
1
7
4
11
14
17
41
44
47
71
74
77
Ответ: 9
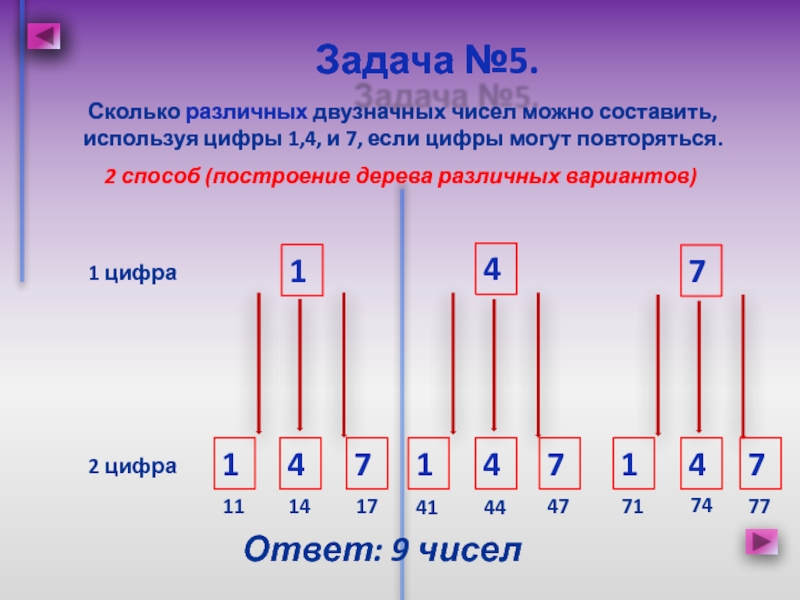
чисел
Слайд 10Сколько различных двузначных чисел можно составить, используя цифры 1,4, и
7, если цифры могут повторяться.
Задача №5.
2 способ (построение дерева
различных вариантов)4
7
4
1
1
7
1 цифра
2 цифра
4
1
7
4
1
7
Ответ: 9 чисел
11
14
17
41
44
47
71
74
77
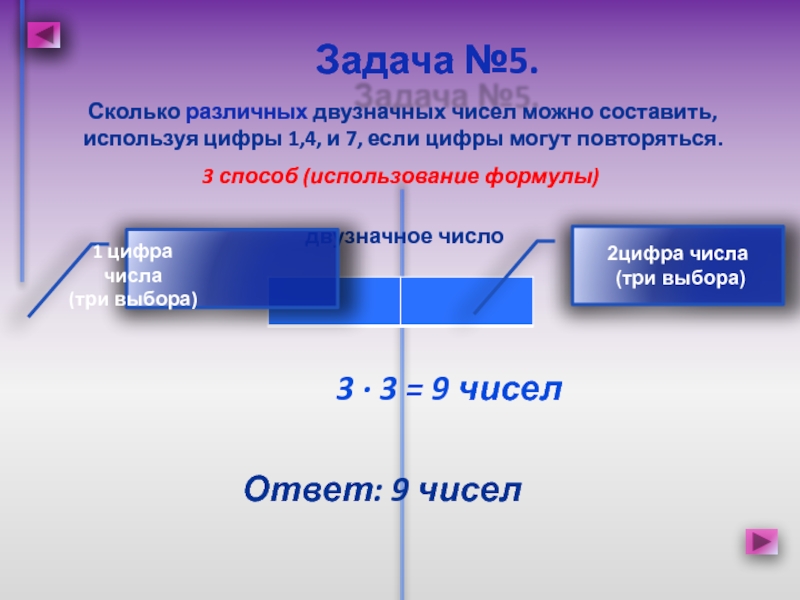
Слайд 11Сколько различных двузначных чисел можно составить, используя цифры 1,4, и
7, если цифры могут повторяться.
Задача №5.
3 способ (использование формулы)
Ответ:
9 чиселдвузначное число
3 · 3 = 9 чисел
2цифра числа
(три выбора)
1 цифра числа
(три выбора)
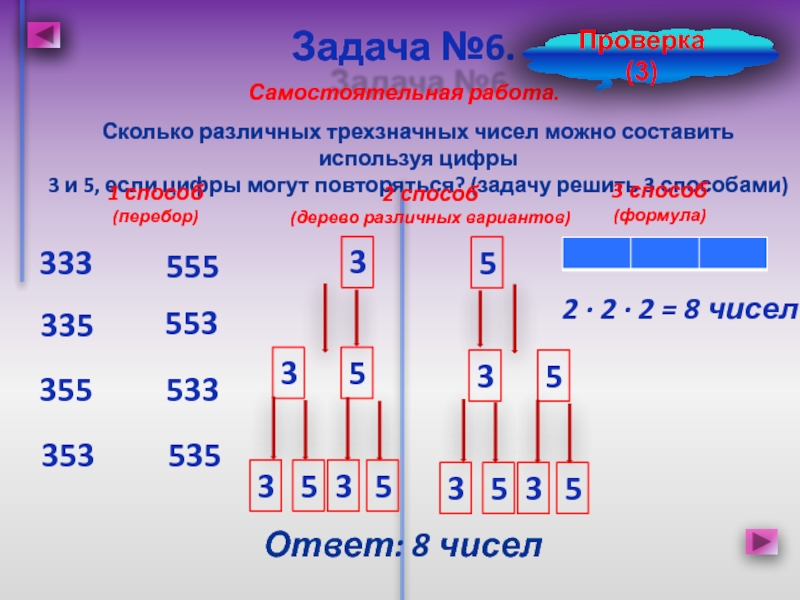
Слайд 12Сколько различных трехзначных чисел можно составить используя цифры
3 и
5, если цифры могут повторяться? (задачу решить 3 способами)
Задача
№6.Самостоятельная работа.
Проверка (3)
1 способ
(перебор)
333
335
355
555
553
533
353
535
2 способ
(дерево различных вариантов)
Ответ: 8 чисел
3
5
3
5
3
5
3
5
5
3
3
5
5
3
3 способ
(формула)
2 · 2 · 2 = 8 чисел
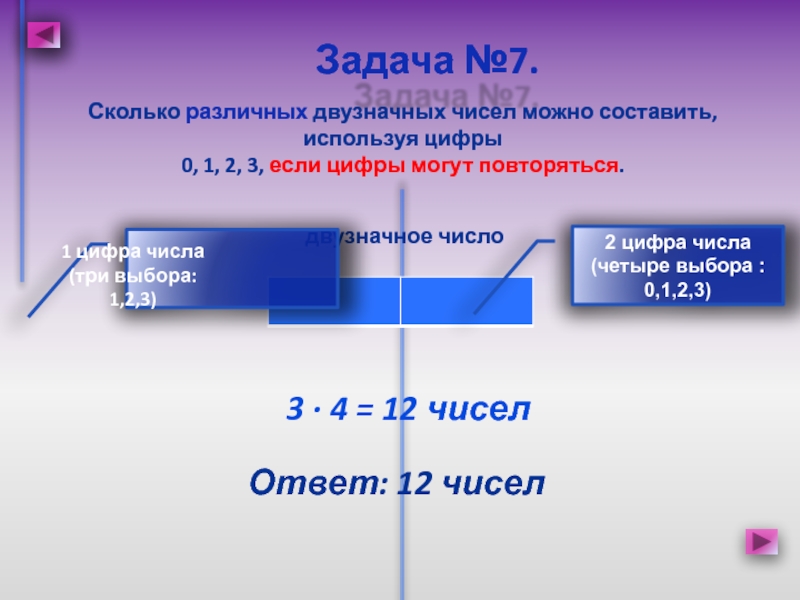
Слайд 13Сколько различных двузначных чисел можно составить, используя цифры
0, 1,
2, 3, если цифры могут повторяться.
Задача №7.
Ответ: 12 чисел
двузначное
число3 · 4 = 12 чисел
2 цифра числа (четыре выбора : 0,1,2,3)
1 цифра числа
(три выбора: 1,2,3)
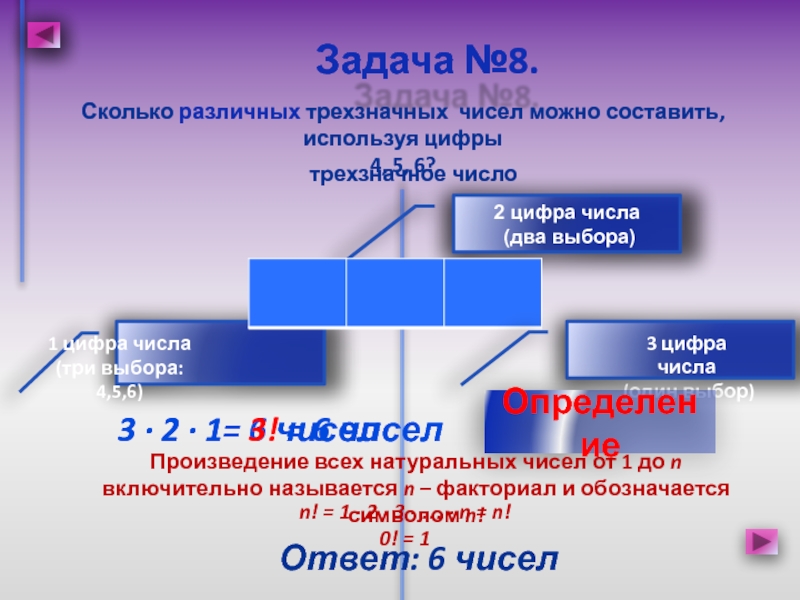
Слайд 14Сколько различных трехзначных чисел можно составить, используя цифры
4, 5,
6?
Задача №8.
Ответ: 6 чисел
трехзначное число
3 · 2 · 1=
6 чисел2 цифра числа
(два выбора)
1 цифра числа
(три выбора: 4,5,6)
3 цифра числа
(один выбор)
Определение
Произведение всех натуральных чисел от 1 до n включительно называется n – факториал и обозначается символом n!
3 · 2 · 1= 3! = 6 чисел
n! = 1 · 2 · 3 · … · n = n!
0! = 1
Слайд 15Комбинаторика – это раздел математики,
посвященный решению задач выбора и
расположения элементов некоторого множества в соответствии с заданными правилами. Комбинаторика
изучает комбинации и перестановки предметов, расположение элементов, обладающее заданными свойствами. Обычный вопрос в комбинаторных задачах: сколькими способами…К комбинаторным задачам относятся также задачи построения математических квадратов, задачи расшифровки и кодирования.
Историческая справка
Слайд 16Рождение комбинаторики как раздела математики связано с трудами великих французских
математиков XVII века Блеза Паскаля и Пьера Ферма, хотя отдельные
понятия и факты комбинаторики были известны ещё математикам античности и средневековья. С 50-х годов XX века интерес к комбинаторике возрождается в связи с бурным развитием кибернетики.Блез Паскаль
1623-1662
Пьер Ферма
1601-1665
Слайд 17 Смыкалова Е. В. Дополнительные главы по математике для учащихся
5 класса. СПб: СМИО Пресс, 2012
Книга для учителя. Сборник
уроков математики / Смыкалова Е.В., редактор составитель – СПб, СМИО Пресс, 2007Чекалина И.П. разработка урока по теме: «Комбинаторика»
Список литературы:
Слайд 18Титульный лист: http://www.mathpages.com/HoME/icombina.htm
Слайд 2: http://pzvezda.ru/alye-rozy-pesnya.html ; http://alfadogy.ru/dizaine/1811-fotostok-cvety-rozy-krasnye-i-alye;
http://mirgif.com/malenkie-animacionnye_kartinki-cvety.htm ; http://teakai.ru/photo/rozy_animacija/4-2-0-0-2 ;
http://www.liveinternet.ru/users/4702264/post235083852/
; http://www.nn-service.ru/cgi-bin/flowers.pl ;
http://www.sevdaselim.net/forums/religious-information-dini-bilgiler/52600.htm; http://blogs.germany.ru/680512/10430453.html ;
http://www.lenagold.ru/fon/clipart/r/roza/gelt.html.
Слайд 3: http://900igr.net/fotografii/matematika/Summa-i-raznost-kubov/002-Ustno.html
Слайд
4: http://capacitacionenlinea.cl/css/%D1%81%D1%83%D0%BF-%D1%81%D0%BE%D0%BB%D1%8F%D0%BD%D0%BA%D0%B0-%D0%BC%D1%8F%D1%81%D0%BD%D0%B0%D1%8F; http://allrecipe.ru/sup_view-1_8.htm ; http://rus-eda.ru/ryba-zapechennaya/ ;http://donduet.gold.dn.ua/catalog/18/16810/page17814.html ; http://veillant.ru/salaty/8487-calat-po-francuzski-s-myasom.html .
Слайд 6: blestiashky.narod.ru ; kartiny.ucoz.ru ; http://mirgif.com/animacija/apelsiny.gif .
Слайд 8: http://radikale.ru/data/upload/05615/04012/cb20f41586.gif
Слайд16: http://hoster.bmstu.ru/~fn1/?page_id=82
Список источников иллюстраций:
