Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение показательных уравнений
Содержание
- 1. Решение показательных уравнений
- 2. 11234
- 3. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯУравнения вида af(x)=ag(x),где a -
- 4. 1. Решаемые переходом к одному основанию.2. Решаемые
- 5. 54x+2 = 12554x+2 =534x+2 = 34 x
- 6. Решение путем деления Если обе части уравнения
- 7. 3х=2х разделим обе части на 2х3х: 2х=2х: 2х(1,5)х=1(1,5)х=(1,5)0 х =0Пример показательного уравнения,которое решается путем деления
- 8. Решение разложением на множителиЕсли одна из частей
- 9. Пример показательного уравнения, одна из частей которого содержит алгебраическую сумму3х+1-2*3х-2=253х-2*(3х+1-(х-2)-2)=253х-2*(33-2)=253х-2*25=253х-2=13х-2=30х-2=0х=2
- 10. Сведение показательных уравнений к квадратным
- 11. Найдите корень уравнения устно:
- 12. Найдите корень уравнения устно:
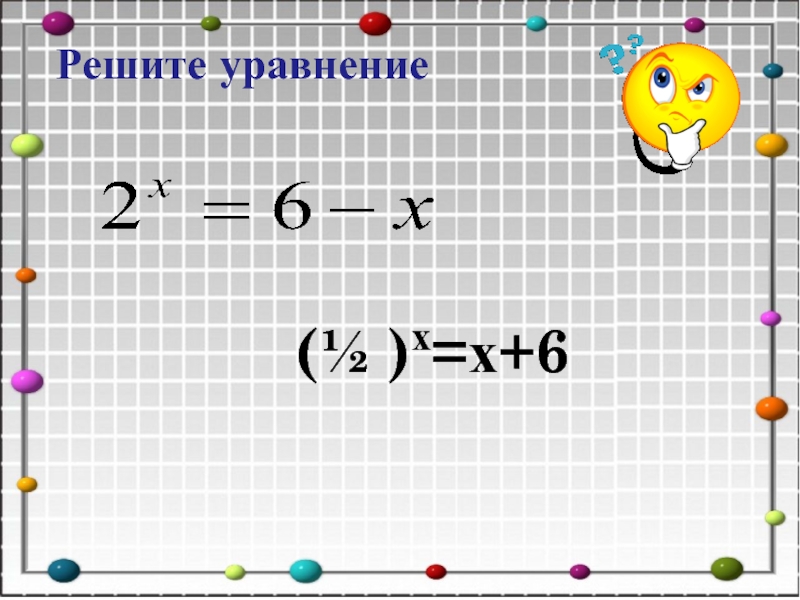
- 13. (½ )х=х+6Решите уравнение
- 14. Скачать презентанцию
11234
Слайды и текст этой презентации
Слайд 3ПОКАЗАТЕЛЬНЫЕ
УРАВНЕНИЯ
Уравнения вида af(x)=ag(x),где
a - положительное число ,
отличное
от 1,и уравнения ,
показательными.Слайд 41. Решаемые переходом к одному основанию.
2. Решаемые переходом к одному
показателю степени.
3. Решаемые вынесением общего множителя за скобку.
4. Сводимые к
квадратным или кубическим введением замены переменной.ОСНОВНЫЕ ВИДЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ
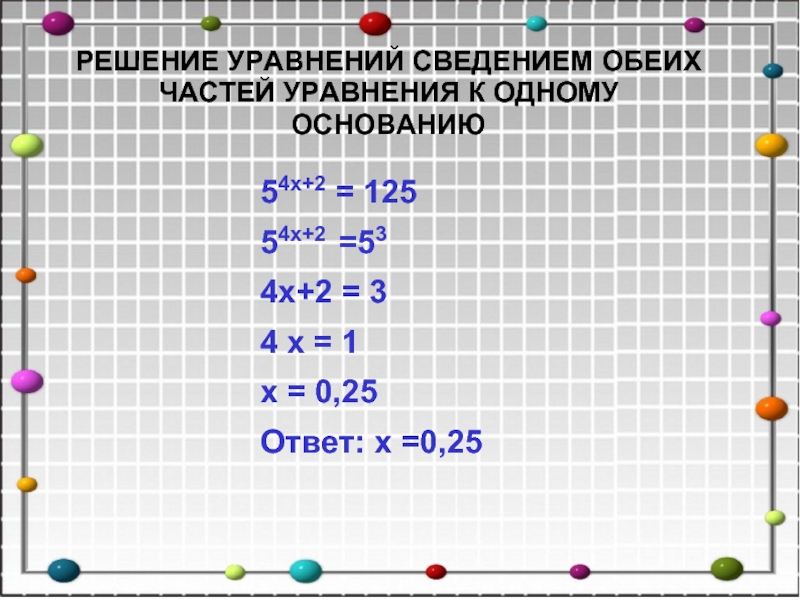
Слайд 554x+2 = 125
54x+2 =53
4x+2 = 3
4 x = 1
x =
0,25
Ответ: x =0,25
РЕШЕНИЕ УРАВНЕНИЙ СВЕДЕНИЕМ ОБЕИХ ЧАСТЕЙ УРАВНЕНИЯ К ОДНОМУ
ОСНОВАНИЮ
Слайд 6Решение путем деления
Если обе части уравнения степени
с равными
показателями ,
то уравнение решают делением
обеих частей на любую
из степеней.Слайд 73х=2х разделим обе части на 2х
3х: 2х=2х: 2х
(1,5)х=1
(1,5)х=(1,5)0
х =0
Пример
показательного уравнения,
которое решается путем деления
Слайд 8Решение разложением на множители
Если одна из частей уравнения содержит алгебраическую
сумму с одинаковыми основаниями , показатели которых отличаются на постоянное
слагаемое , то такое уравнение решается разложением на множители.Слайд 9Пример показательного уравнения, одна из частей которого содержит алгебраическую сумму
3х+1-2*3х-2=25
3х-2*(3х+1-(х-2)-2)=25
3х-2*(33-2)=25
3х-2*25=25
3х-2=1
3х-2=30
х-2=0
х=2
Слайд 10Сведение показательных уравнений к квадратным
Одним из наиболее
распространенных методов решения уравнений (в том числе и показательных) является
метод замены переменной, позволяющий свести то или иное уравнение к алгебраическому (как правило, квадратному) уравнению.x
Теги