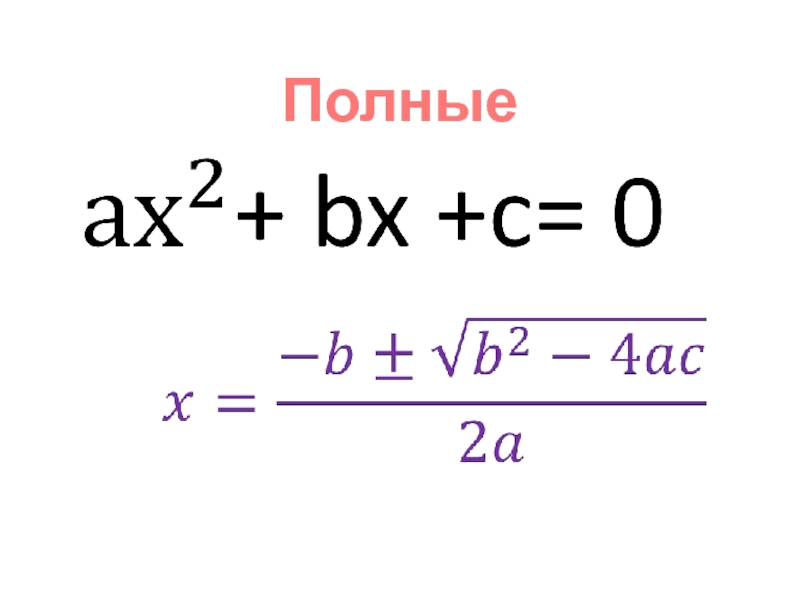"Уравнения, обобщающий урок"

Содержание

1. "Уравнения, обобщающий урок"
2. Через математические знания, полученные в школе, лежит
3. Содержание Виды уравнений2) Линейные уравнения3) Квадратные уравнения4) Биквадратные уравнения
4. Виды уравнений:-линейные;-квадратные;- биквадратные- дробно-линейные
5. Определение: уравнение вида а х =
6. Отличительная особенность такого уравнения – переменная х входит в уравнение обязательно в первой степени.
7. 5(11 – х) = 20х = 7-
8. 5(x-1)+8=1–3(x+2)Линейные уравнения
9. Решить уравнение – это значит найти все
10. Алгоритм решения уравненияУпростить, раскрыть скобки, избавиться от
11. Раскрытие скобокЕсли перед скобками стоит знак «
12. Раскрытие скобокЕсли перед скобками стоит знак «
13. 5(x-1)+8=1–3(x+2)
14. Проверь себя! 1 вариант4(х
15. Разделить обе части уравнения на коэффици-ент при
16. Квадратные уравненияНеполныеПолные
17. Определение квадратного уравнения.Опр. 1. Квадратным уравнением называется
18. Решение квадратных уравненийНеполные квадратные уравнения
19. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ.b=0, C=0b≠0, c=0b=0,c≠0
20. Неполные
21. а)Найти дискриминантб) Найти корни квадратного уравнения
22. Полные
23. Квадратное уравнение Уравнение ax2+bx+c=0, где a ≠ 0, называется квадратным уравнением
24. Скачать презентанцию

Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий.

Главная
Математика
"Уравнения, обобщающий урок"

Слайды и текст этой презентации

Слайд 1Уравнения.
Обобщение темы

Слайд 2Через математические знания,
полученные в школе,
лежит широкая дорога к

огромным,
почти необозримым
областям труда и открытий.

А.И. Маркушевич.

Слайд 3Содержание
Виды уравнений
2) Линейные уравнения
3) Квадратные уравнения
4) Биквадратные
уравнения

Слайд 4Виды уравнений:
-линейные;
-квадратные;
- биквадратные
- дробно-линейные

Слайд 5Определение: уравнение вида а х = в (где х

– переменная, а и в – некоторые числа) называется линейным

уравнением с одной переменной.

Линейные уравнения

Определение: уравнение вида а х = в (где х – переменная, а и в – некоторые

Слайд 6Отличительная особенность такого уравнения – переменная х входит в уравнение

обязательно в первой степени.

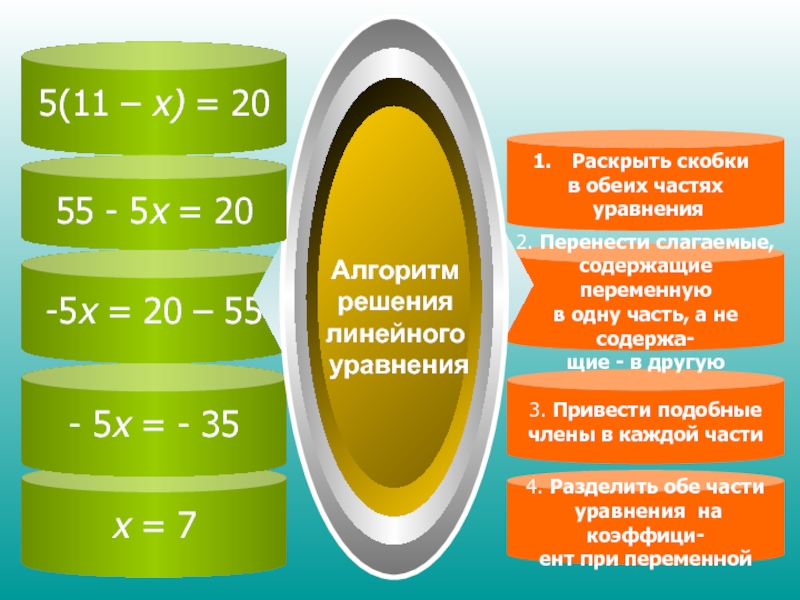
Слайд 75(11 – х) = 20
х = 7
- 5х = -

35
-5х = 20 – 55
4. Разделить обе части
уравнения на

коэффици-
ент при переменной

3. Привести подобные
члены в каждой части

2. Перенести слагаемые,
содержащие переменную
в одну часть, а не содержа-
щие - в другую

Раскрыть скобки
в обеих частях
уравнения

Алгоритм
решения
линейного
уравнения

5(11 – х) = 20х = 7- 5х = - 35-5х = 20 – 554. Разделить обе

Слайд 85(x-1)+8=1–3(x+2)
Линейные уравнения

Слайд 9Решить уравнение – это значит найти все его корни или

доказать, что корней нет.
Корнем уравнения с одной переменной называется значение

переменной, при котором уравнение обращается в верное равенство.

Решить уравнение – это значит найти все его корни или доказать, что корней нет.Корнем уравнения с одной

Слайд 10Алгоритм решения уравнения
Упростить, раскрыть скобки, избавиться от знаменателя.
Перенести слагаемые, содержащие

переменную, в левую часть уравнения, а числа без переменной –

в правую часть.
Упростить, привести подобные слагаемые.
Разделить на коэффициент при неизвестном.
Записать ответ.

Алгоритм решения уравненияУпростить, раскрыть скобки, избавиться от знаменателя.Перенести слагаемые, содержащие переменную, в левую часть уравнения, а числа

Слайд 11Раскрытие скобок
Если перед скобками стоит знак « +», то скобки

можно опустить, сохранив знак каждого слагаемого, заключенного в скобки.

Пример.
(25 –3х) + (–2х + 6) = 25 – 3х – 2х + 6 =
= 31 – 5х.

Раскрытие скобокЕсли перед скобками стоит знак « +», то скобки можно опустить, сохранив знак каждого слагаемого, заключенного

Слайд 12Раскрытие скобок
Если перед скобками стоит знак « -», то скобки

можно опустить, изменив знак каждого слагаемого, заключенного в скобки.

( 6х – 3) – ( 14 – 2х) = 6х – 3 –14 + 2х =
= 8х – 17;
12 + ( х – 3) – (– 3х + 1) = 12 + х – 3 +3х –
– 1 = 8 + 4х.

Раскрытие скобокЕсли перед скобками стоит знак « -», то скобки можно опустить, изменив знак каждого слагаемого, заключенного

Слайд 135(x-1)+8=1–3(x+2)

Слайд 14Проверь себя!

1 вариант
4(х – 11) –

5(2х – 7)=0

4х – 44 – 10х +

35 = 0,
-6х – 9 = 0,
-6х = 9,
х = 9 : (-6),
х = -1,5

2 вариант
2(3х + 7) – 8(х + 3)=0

6x + 14 – 8x – 24 = 0,
-2x – 10 = 0,
-2x = 10,
x = 10 : (-2),
x = -5

Проверь себя! 1 вариант4(х – 11) – 5(2х – 7)=0 4х – 44

Слайд 15Разделить обе части
уравнения на коэффици-
ент при переменной
Привести подобные
члены

в каждой части
Перенести слагаемые,
содержащие переменную
в одну часть,

а не содержа-
щие - в другую

Раскрыть скобки
в обеих частях
уравнения

Разделить обе части уравнения на коэффици-ент при переменнойПривести подобные члены в каждой части Перенести слагаемые, содержащие переменную

Слайд 16Квадратные уравнения
Неполные
Полные

Слайд 17Определение квадратного уравнения.
Опр. 1. Квадратным уравнением называется уравнение вида ах2

+ bх + с = 0, где х –переменная, а,

b и с - некоторые числа, причем а  0.
Числа а, b и с - коэффициенты квадратного уравнения. Число а называют первым коэффициентом, b – вторым коэффициентом и с – свободным членом.