Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач. Окружность и круг. ГМТ 7 класс
Содержание
- 1. Решение задач. Окружность и круг. ГМТ 7 класс
- 2. 8924252611121314151718282919211234561016207Задания на проверку теоретических знанийТеорияГМТ. Окружность и кругСвойства окружности. Касательная к окружности222723Описанная и вписанная окружности треугольника30
- 3. Геометрическое место точекГМТГеометрическим местом точек(ГМТ)называют множество всех точек,обладающих определённымсвойством.
- 4. Серединный перпендикуляротрезка как ГМТСЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯРотрезка является геометрическим местом точек, равноудалённых от концов этого отрезкаА
- 5. Биссектриса угла как ГМТБИССЕКТРИСА угла являетсягеометрическим местом точек,принадлежащих углу и равноудалённыхот его сторонА
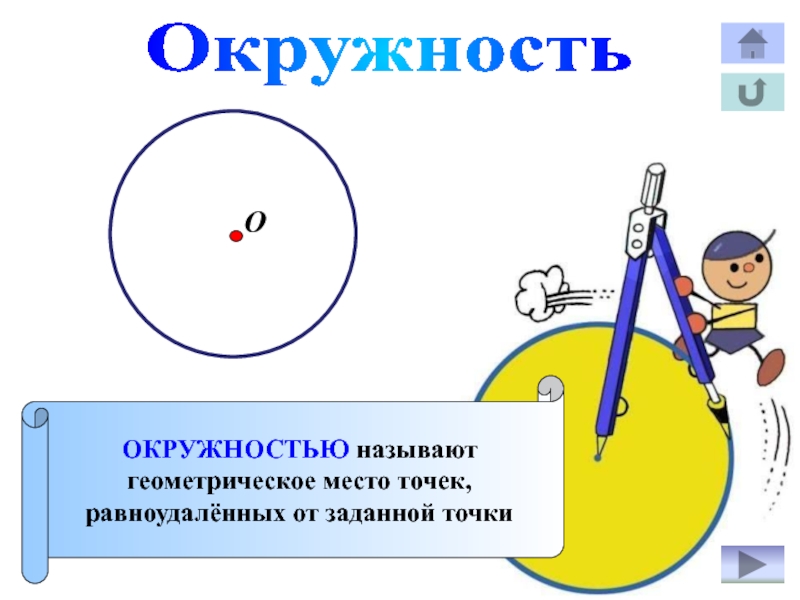
- 6. ОкружностьОКРУЖНОСТЬЮ называютгеометрическое место точек,равноудалённых от заданной точкиО
- 7. КругКРУГОМ называютгеометрическое место точек, расстояние от которых до заданной точки не большеданного положительного числаО
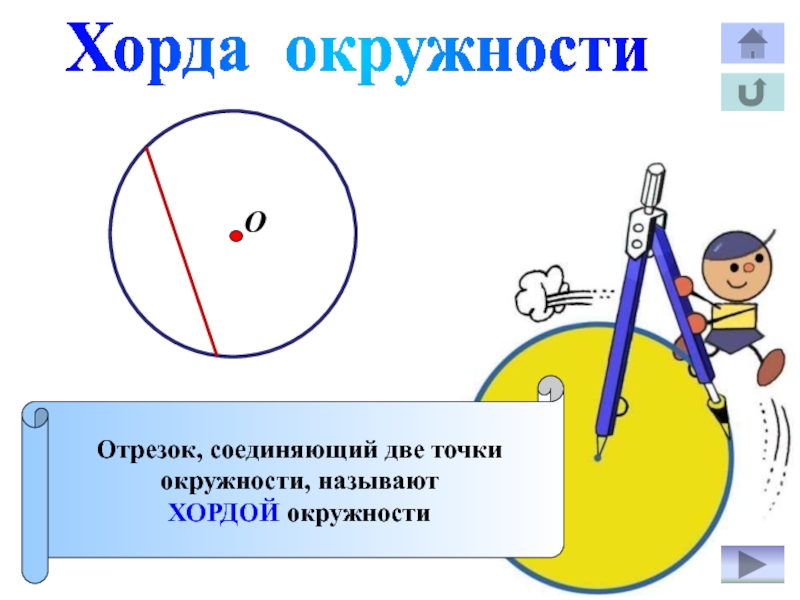
- 8. Хорда окружностиОтрезок, соединяющий две точкиокружности, называютХОРДОЙ окружностиО
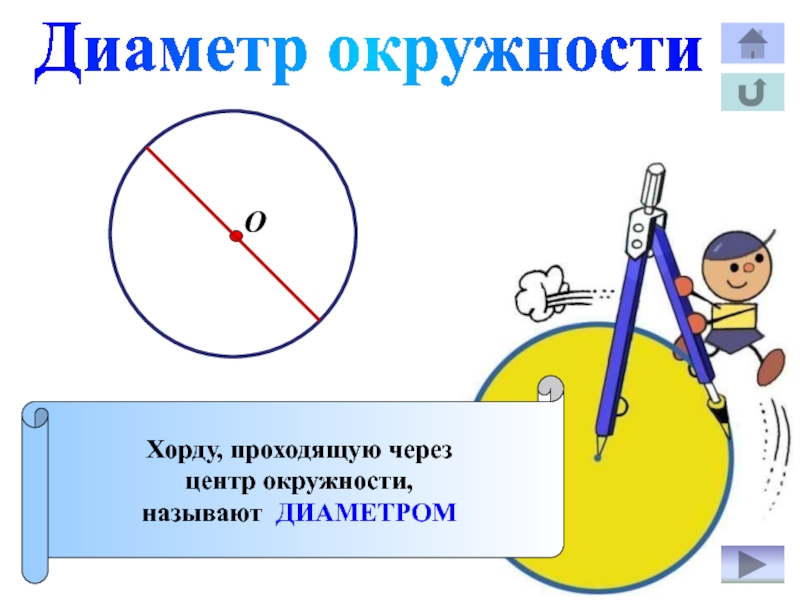
- 9. Диаметр окружностиХорду, проходящую через центр окружности,называют ДИАМЕТРОМО
- 10. Свойства окружностиДиаметр окружности, перпендикулярныйхорде, делит эту хорду
- 11. Касательная к окружностиОПрямую, имеющую с окружностью только одну общую точку называютКАСАТЕЛЬНОЙ к окружности
- 12. Свойство касательнойОКасательная к окружностиперпендикулярна радиусу,проведённому в точку касания
- 13. Признак касательной - 1ОЕсли прямая, проходящая через
- 14. Признак касательной - 2ОЕсли расстояние от центра
- 15. Признак касательной - 2ОЕсли расстояние от центра
- 16. АСвойство отрезков касательных к окружности, проведённых из
- 17. Окружность, описанная около треугольникаООкружность называют описанной околотреугольника, если она проходит черезвсе вершины этого треугольника
- 18. Центр окружности, описанной около треугольникаОЦентр окружности описанной околотреугольника, - это точка пересечениясерединных перпендикуляров его сторон
- 19. Окружность, вписанная в треугольникООкружность называют вписанной втреугольник, если она касаетсявсех его сторон
- 20. Центр окружности, вписанной в треугольникОЦентр окружности, вписанной втреугольник, - это точка пересеченияего биссектрис
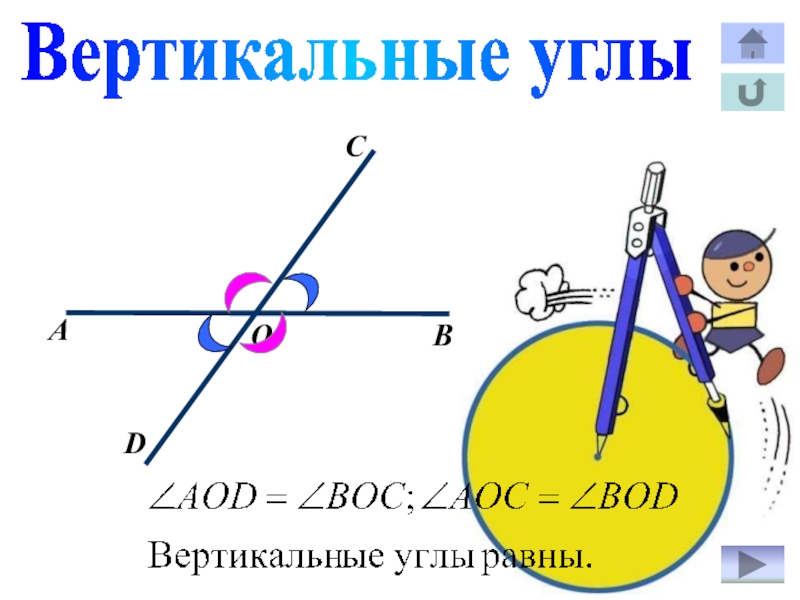
- 21. ВАОCDВертикальные углы
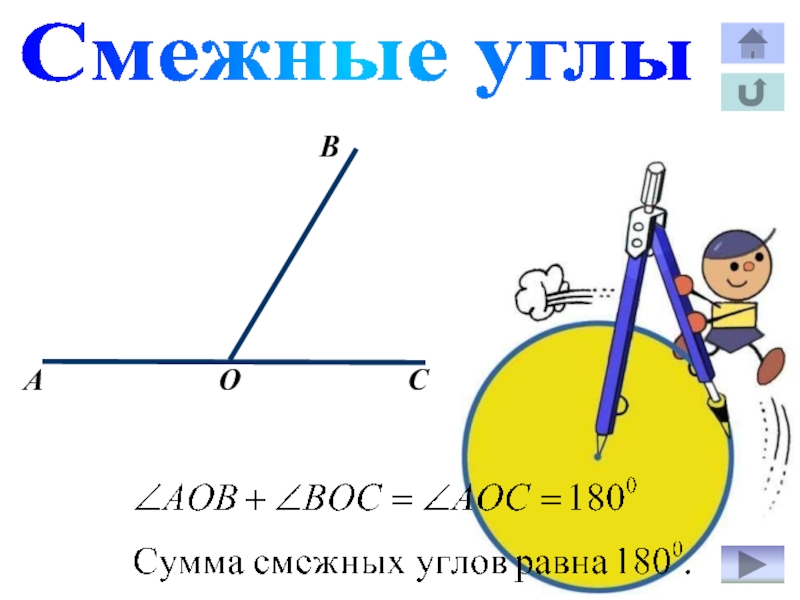
- 22. ВАОCСмежные углы
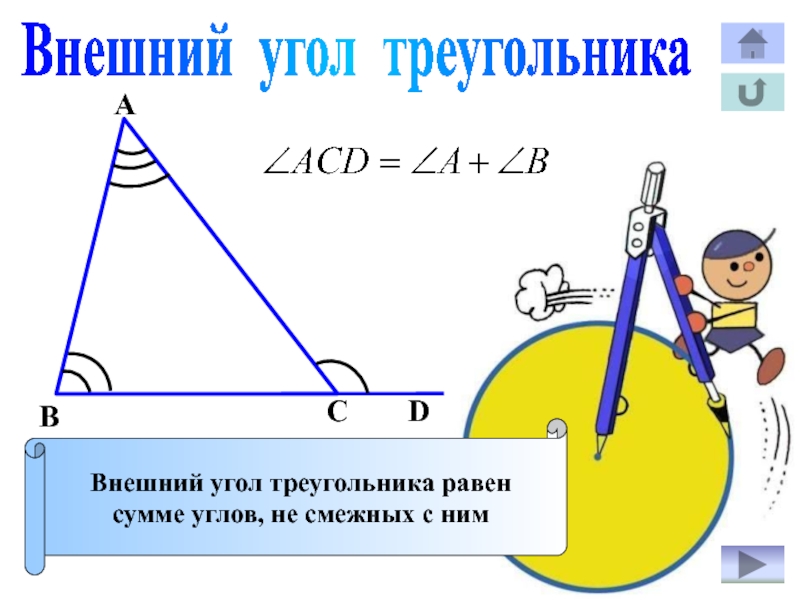
- 23. Внешний угол треугольникаАСВDВнешний угол треугольника равенсумме углов, не смежных с ним
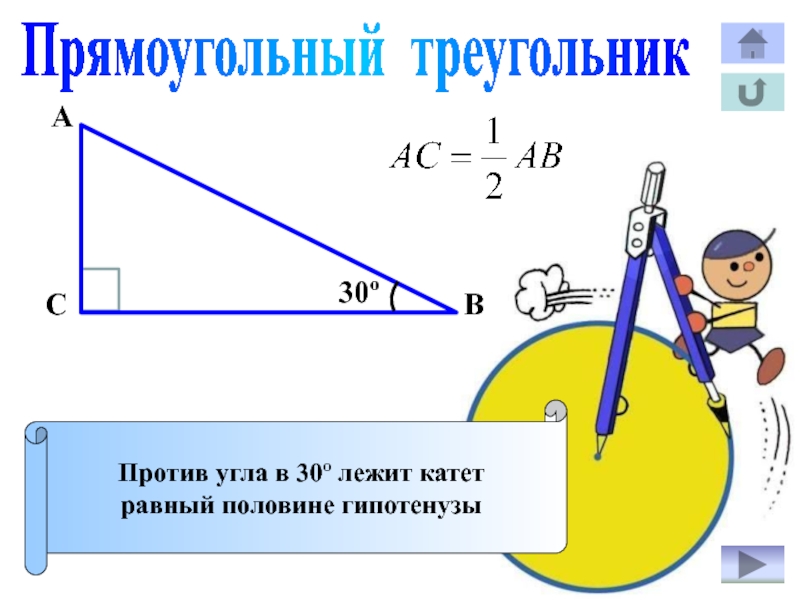
- 24. Прямоугольный треугольникАВС30ºПротив угла в 30º лежит катетравный половине гипотенузы
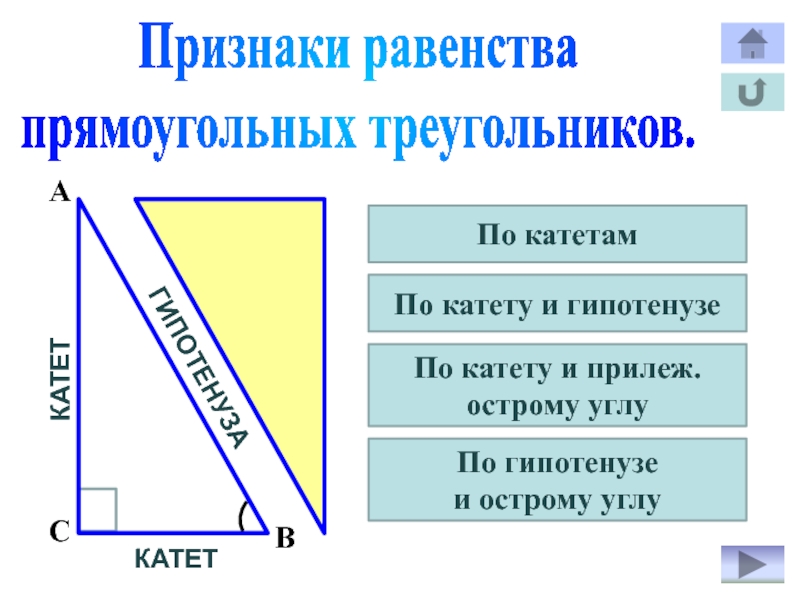
- 25. Признаки равенствапрямоугольных треугольников.АСВКАТЕТКАТЕТГИПОТЕНУЗАПо катетамПо катету и гипотенузеПо катету и прилеж.острому углуПо гипотенузе и острому углу
- 26. Свойстваравнобедренного треугольника.АМВКСNУглы приосновании.Медиана, высота,биссектриса.
- 27. Тестовые задания напроверку теоретических знаний.Необходимо выбрать правильный ответ.891234567
- 28. 1.ВСсАКДаны три точки, не лежащие наодной прямой.
- 29. 2.ВСсАДаны три точки, лежащие наодной прямой. Сколько
- 30. 3.ВОсАКСколько точек содержит геометрическое место точек, принадлежащих
- 31. 4.сТочка К принадлежит окружностис центром в точке
- 32. 5.ОСсАПрямая имеет две общие точки сокружностью с
- 33. 6.сНа окружности отметили точку В,Х – произвольная
- 34. 7. Какое утверждение верно?Подумай!Если
- 35. OВАКМПостроение (2)
- 36. OВАКМПостроение (2)
- 37. OКМRRПостроение
- 38. OВАКМПостроение
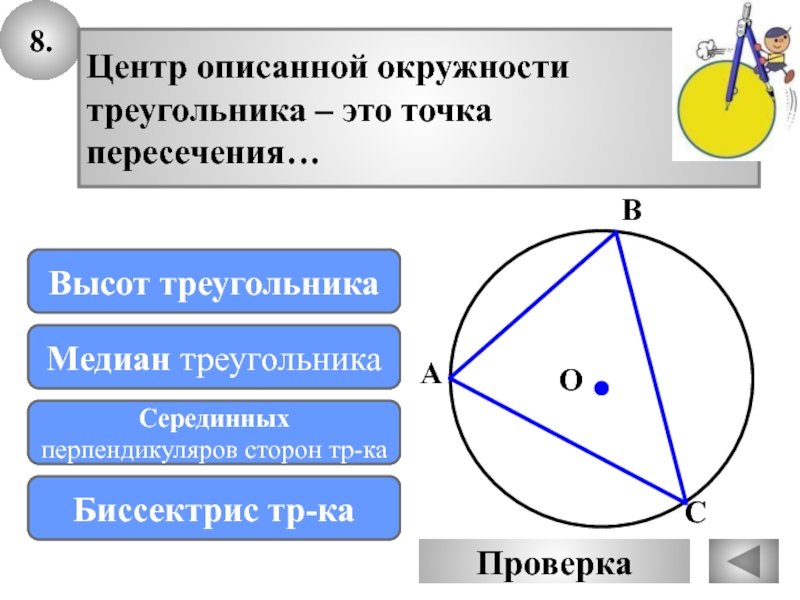
- 39. 8.Центр описанной окружности треугольника – это точка пересечения…Подумай!Высот треугольника Подумай!Медиан треугольникаМОЛОДЕЦСерединных перпендикуляров сторон тр-каПодумай!Биссектрис тр-каАOПроверка ВС
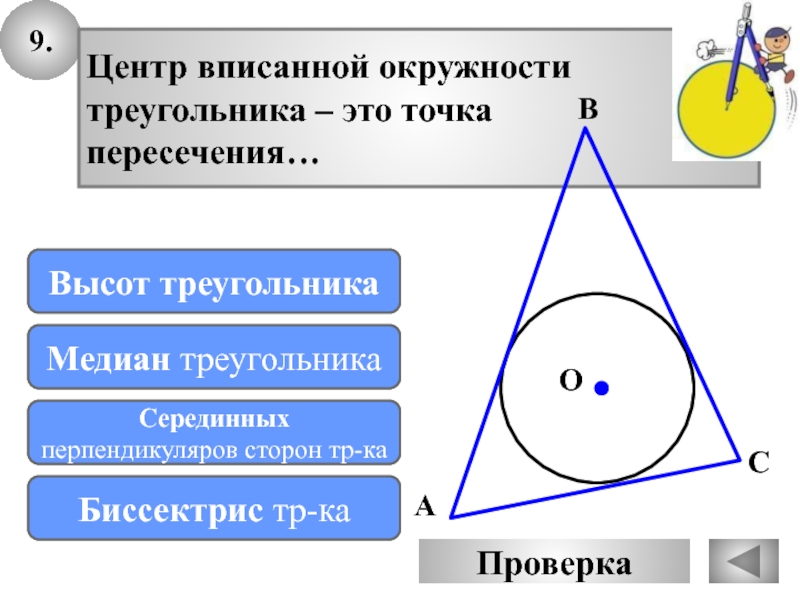
- 40. 9.Центр вписанной окружности треугольника – это точка пересечения…Подумай!Высот треугольника Подумай!Медиан треугольникаМОЛОДЕЦБиссектрис тр-каПодумай!Серединных перпендикуляров сторон тр-каАOПроверка ВС
- 41. Геометрическое место точек.Окружность и круг.171810111213141516
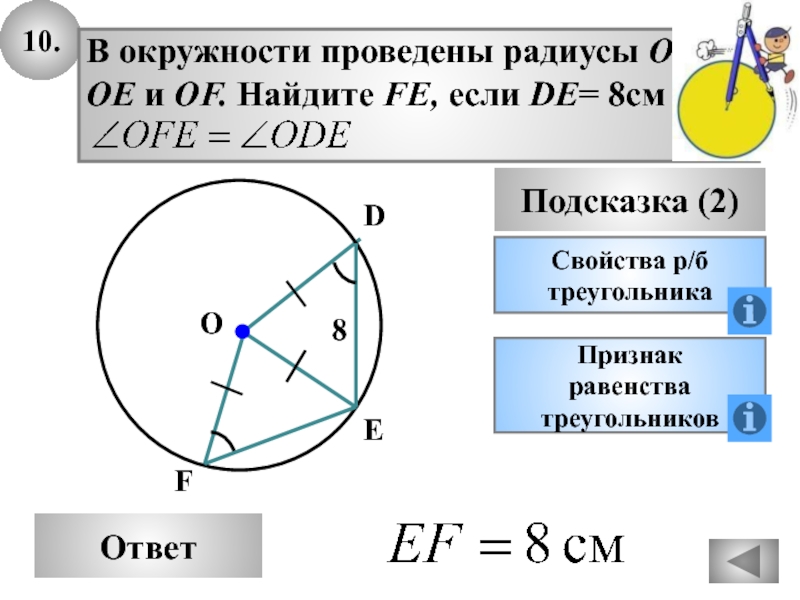
- 42. 10.ОтветПодсказка (2)Свойства р/бтреугольникаПризнак равенстватреугольниковED8FO
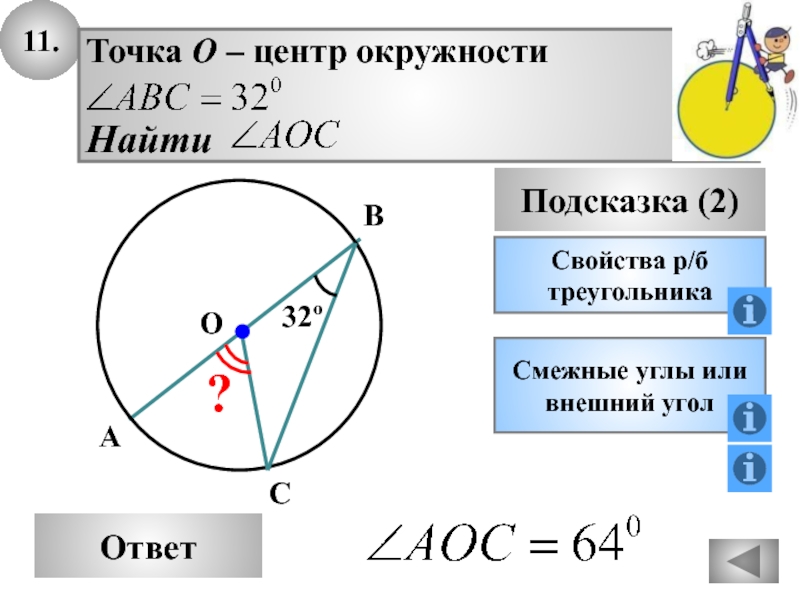
- 43. 11.ОтветПодсказка (2)Свойства р/бтреугольникаСмежные углы иливнешний уголСВ32ºАO?
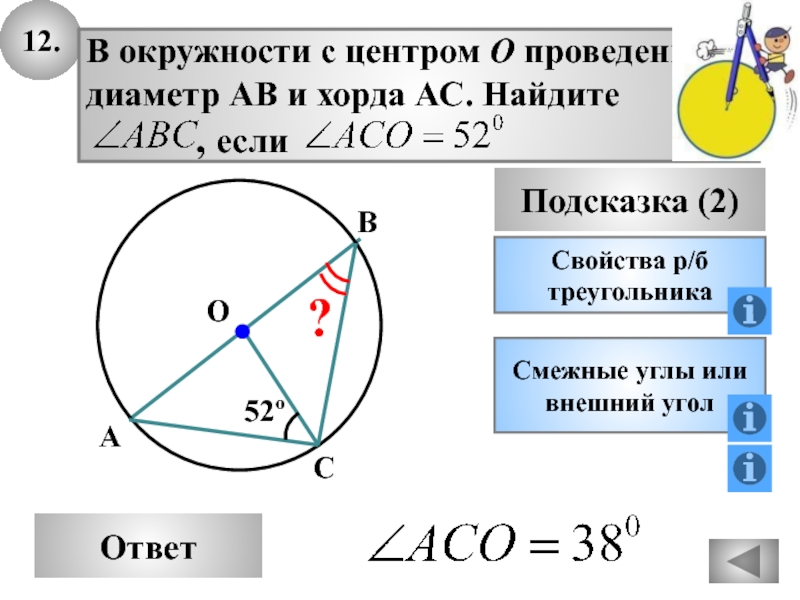
- 44. 12.ОтветПодсказка (2)Свойства р/бтреугольникаСмежные углы иливнешний уголСВ52ºАO?
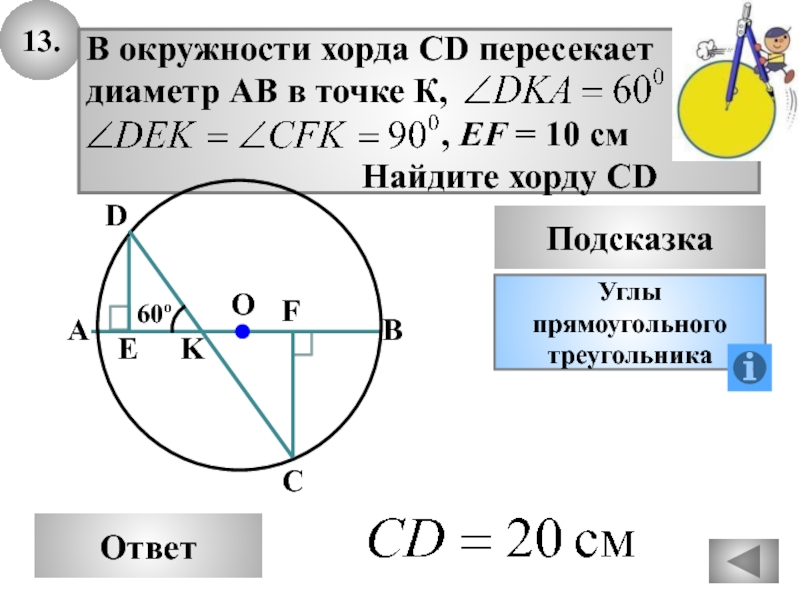
- 45. 13.ОтветПодсказкаУглы прямоугольноготреугольникаСВАODFEK60º
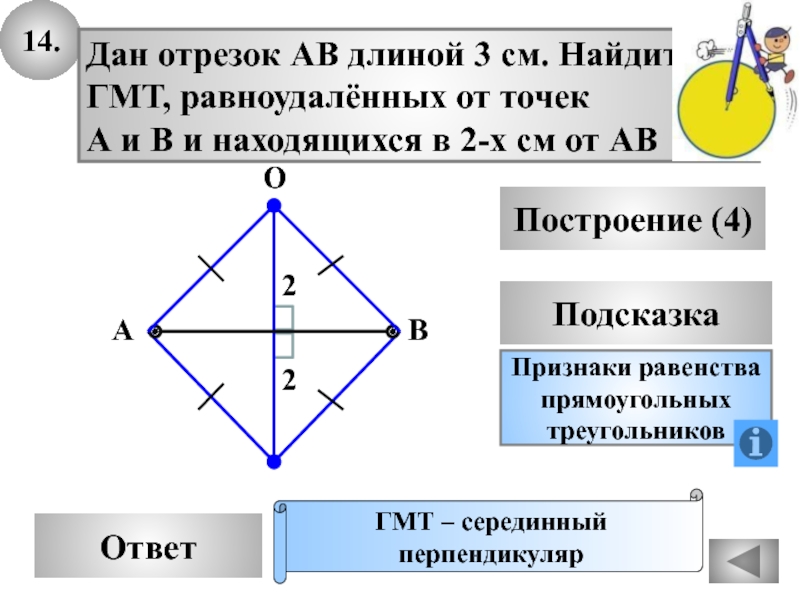
- 46. 14.Дан отрезок АВ длиной 3 см. НайдитеГМТ,
- 47. 15.Ответ (3)ПодсказкаГМТНайдите ГМТ, расстояние от которыхдо центра
- 48. 16.Ответ (4)ПодсказкаГМТПрямые а и b пересекаются. НайдитеГМТ,
- 49. 17.Ответ (2)ПодсказкаГМТДаны точки А и В. Найдите
- 50. 18.Ответ (3)ПодсказкаГМТДаны две параллельные прямые,расстояние между которыми
- 51. Некоторые свойства окружности.Касательная к окружности.1920212223
- 52. 19.ОтветПодсказкаРавенствопрямоуг. тр-овПрямая касается окружности с центромО в
- 53. Равнобедренныйтреугольник20.ОтветПодсказка (3)Определить уголОВАНа рисунке прямая ВС касаетсяокружности
- 54. 21.ОтветПодсказкаВыполнить дополнительное построениеНа рисунке две окружности имеютобщий
- 55. 22.ОтветНа рисунке две окружности имеютобщий центр. Через
- 56. 23.ОтветНа рисунке прямые АЕ, AF и ВСкасаются
- 57. Описанная и вписаннаяокружности треугольника24252627282930
- 58. Равнобедренныйтреугольник…24.ВыводПодсказкаЦентр описаннойокружностиТочка пересечения медиан АМ и ВКтреугольника
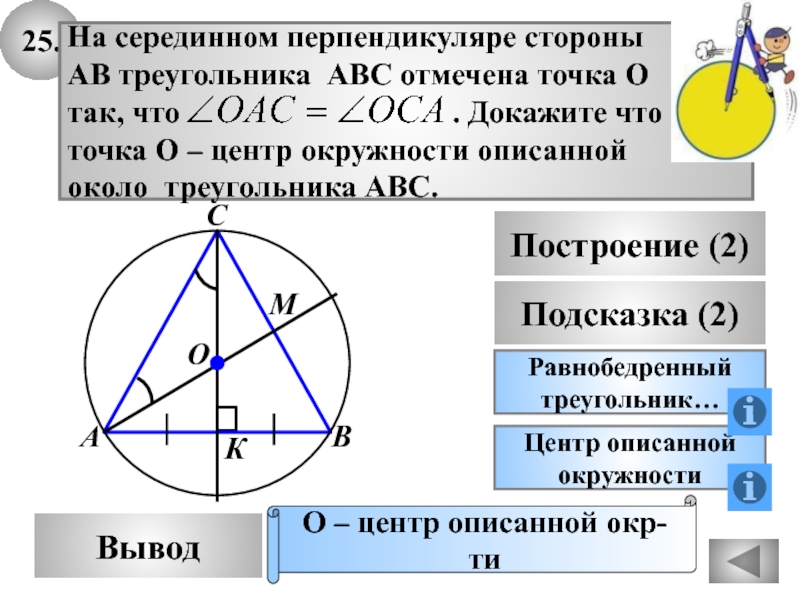
- 59. Равнобедренныйтреугольник…25.ВыводПодсказка (2)Центр описаннойокружностиНа серединном перпендикуляре стороны АВ
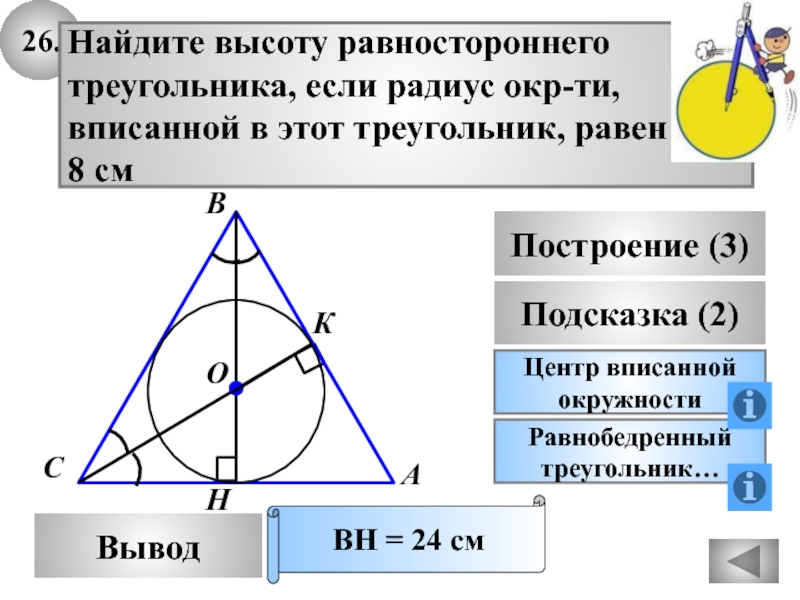
- 60. Равнобедренныйтреугольник…26.ВыводПодсказка (2)Центр вписаннойокружностиНайдите высоту равностороннеготреугольника, если радиус
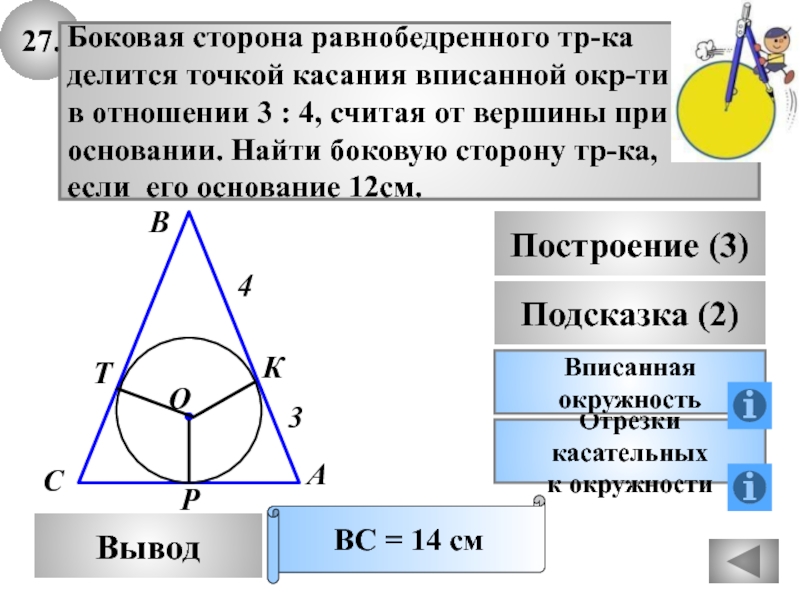
- 61. Отрезки касательныхк окружности27.ВыводПодсказка (2)ВписаннаяокружностьБоковая сторона равнобедренного тр-каделится
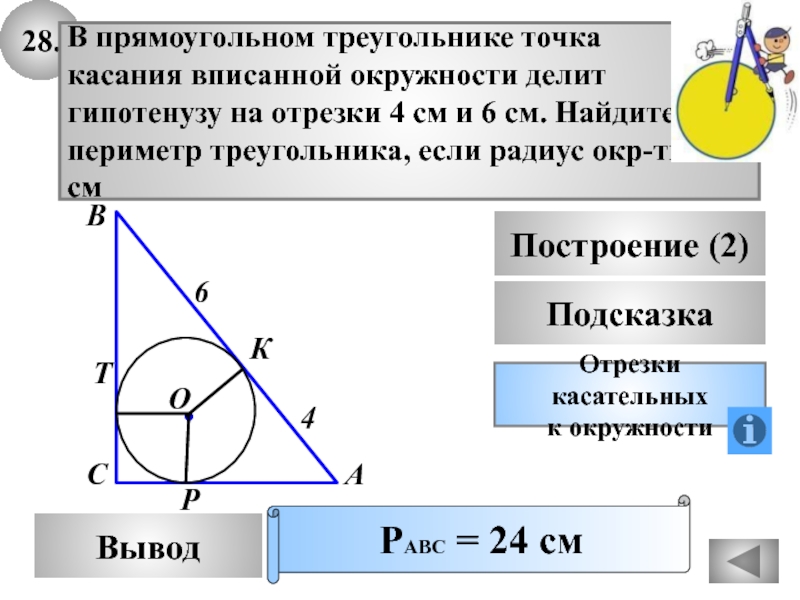
- 62. Отрезки касательныхк окружности28.ВыводПодсказкаВ прямоугольном треугольнике точкакасания вписанной
- 63. Отрезки касательныхк окружности29.ВыводПодсказка (2)ВписаннаяокружностьК окружности, вписанной в
- 64. Отрезки касательныхк окружности30.ПодсказкаОкружность, вписанная в треугольник АВС,Касается
- 65. Используемые ресурсы:4. «Геометрия 7»: Учеб. для учащихся
- 66. Скачать презентанцию
Слайды и текст этой презентации
Слайд 28
9
24
25
26
11
12
13
14
15
17
18
28
29
19
21
1
2
3
4
5
6
10
16
20
7
Задания на проверку теоретических знаний
Теория
ГМТ. Окружность и круг
Свойства окружности. Касательная
к окружности
22
27
23
Описанная и вписанная окружности треугольника
30
Слайд 3Геометрическое место точек
ГМТ
Геометрическим местом точек
(ГМТ)
называют множество всех точек,
обладающих определённым
свойством.
Слайд 4Серединный перпендикуляр
отрезка как ГМТ
СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
отрезка является геометрическим
местом точек, равноудалённых
от концов этого отрезка
А
Слайд 5Биссектриса угла как ГМТ
БИССЕКТРИСА угла является
геометрическим местом точек,
принадлежащих углу и
равноудалённых
от его сторон
А
Слайд 7Круг
КРУГОМ называют
геометрическое место точек, расстояние
от которых до заданной точки
не больше
данного положительного числа
О
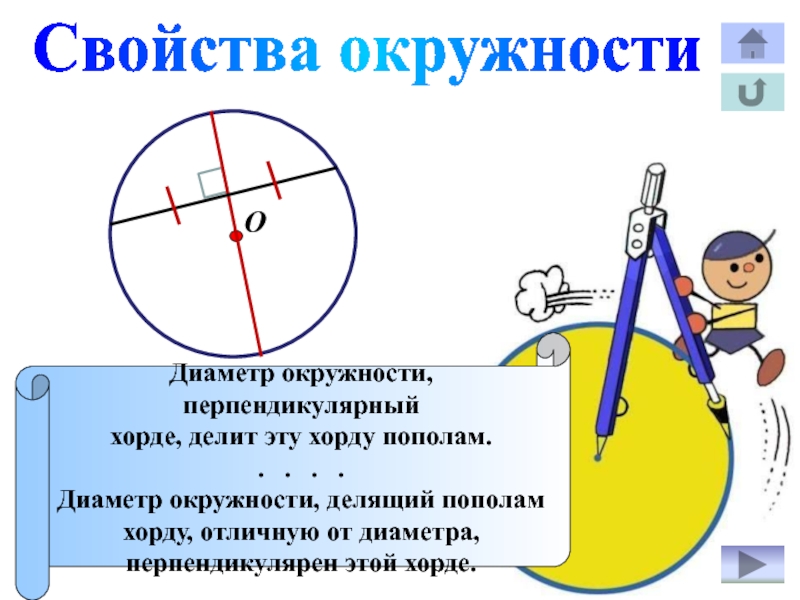
Слайд 10Свойства окружности
Диаметр окружности, перпендикулярный
хорде, делит эту хорду пополам.
. .
. .
Диаметр окружности, делящий пополам
хорду, отличную от диаметра,
перпендикулярен
этой хорде.О
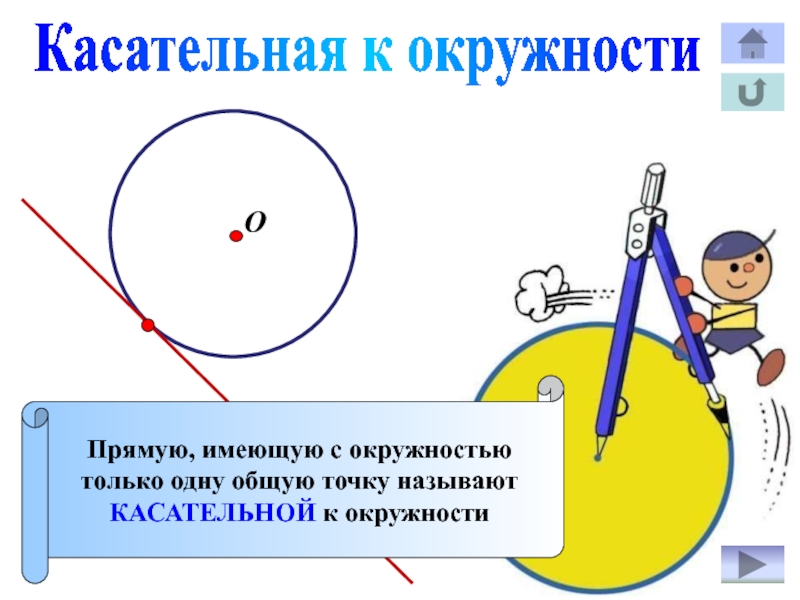
Слайд 11Касательная к окружности
О
Прямую, имеющую с окружностью
только одну общую точку
называют
КАСАТЕЛЬНОЙ к окружности
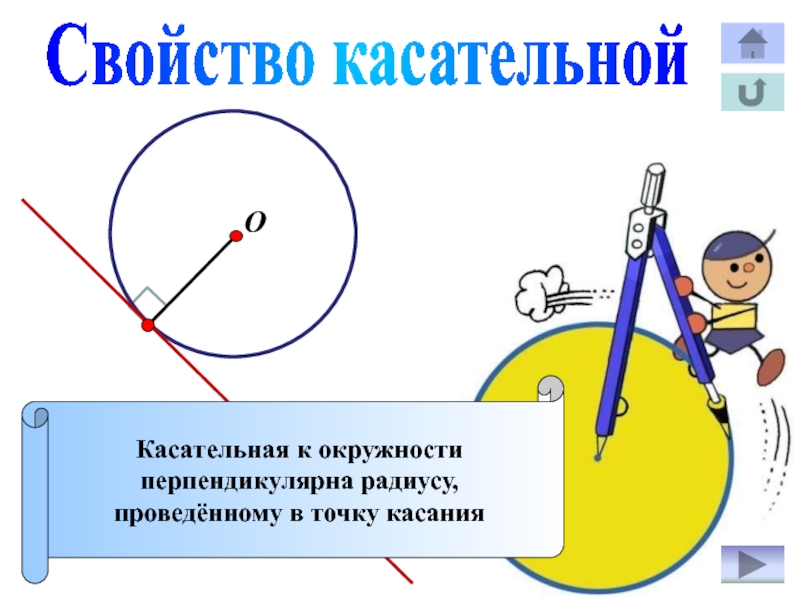
Слайд 12Свойство касательной
О
Касательная к окружности
перпендикулярна радиусу,
проведённому в точку касания
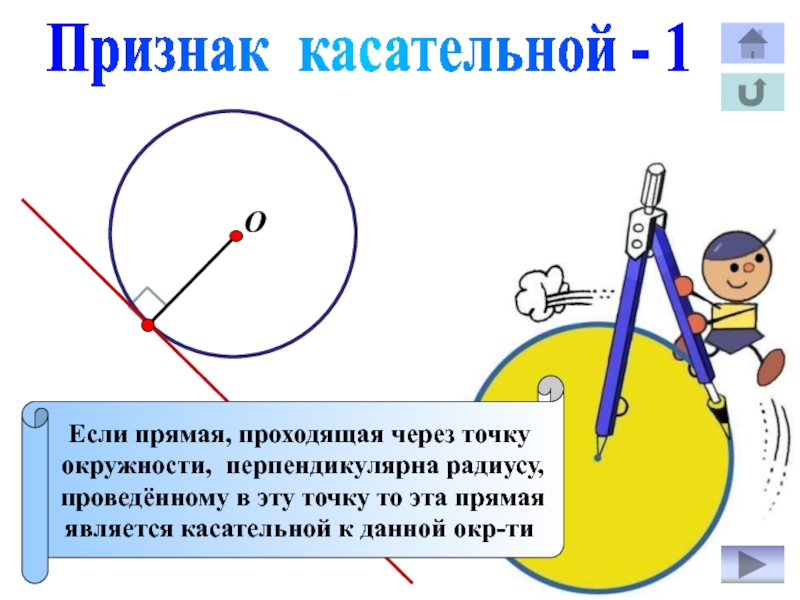
Слайд 13Признак касательной - 1
О
Если прямая, проходящая через точку
окружности, перпендикулярна радиусу,
проведённому
в эту точку то эта прямая
является касательной к данной окр-ти
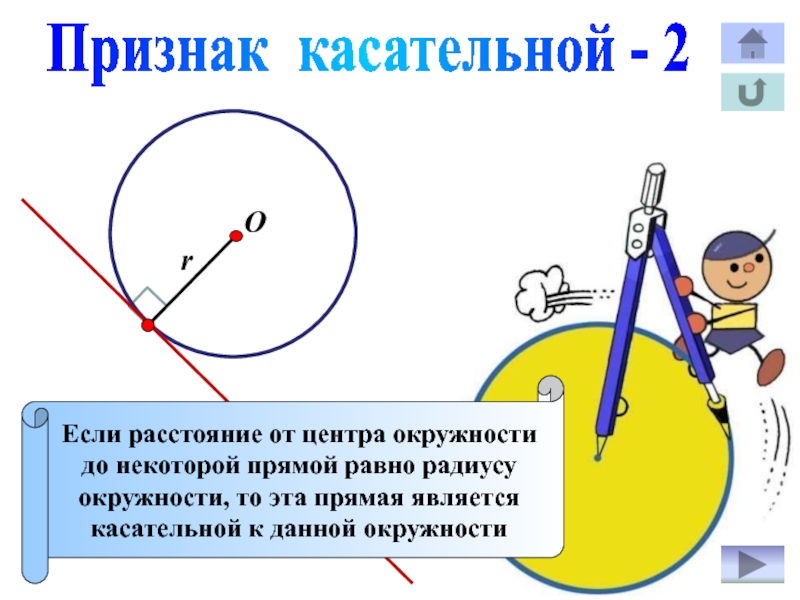
Слайд 14Признак касательной - 2
О
Если расстояние от центра окружности
до некоторой прямой
равно радиусу
окружности, то эта прямая является
касательной к данной окружности
r
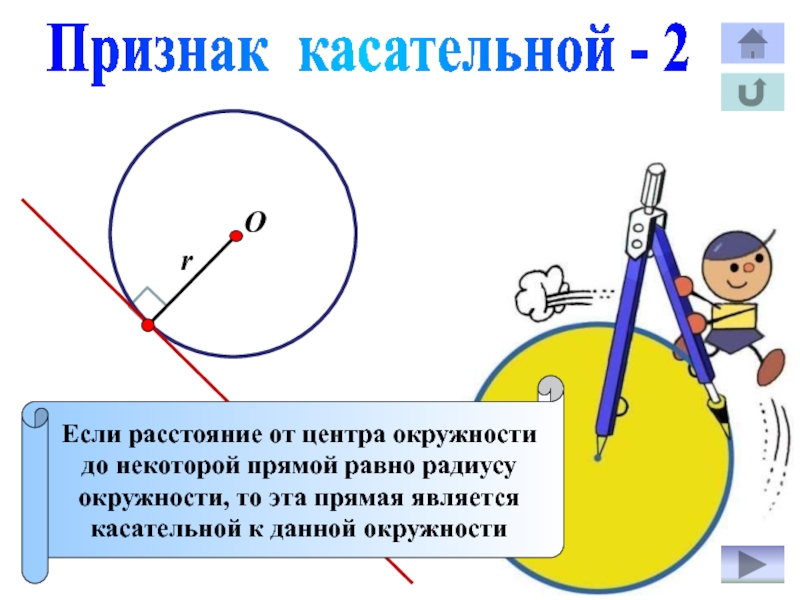
Слайд 15Признак касательной - 2
О
Если расстояние от центра окружности
до некоторой прямой
равно радиусу
окружности, то эта прямая является
касательной к данной окружности
r
Слайд 16А
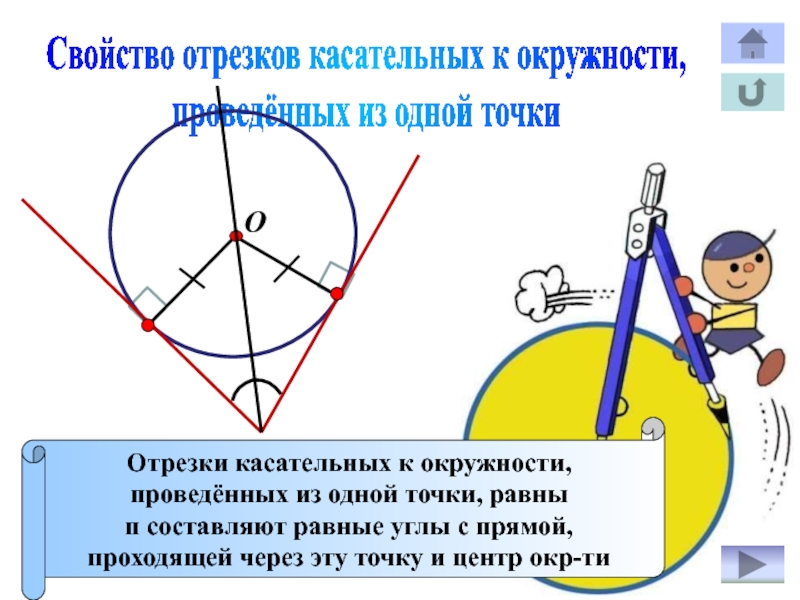
Свойство отрезков касательных к окружности,
проведённых из одной точки
О
Отрезки касательных
к окружности,
проведённых из одной точки, равны
п составляют равные углы с
прямой,проходящей через эту точку и центр окр-ти
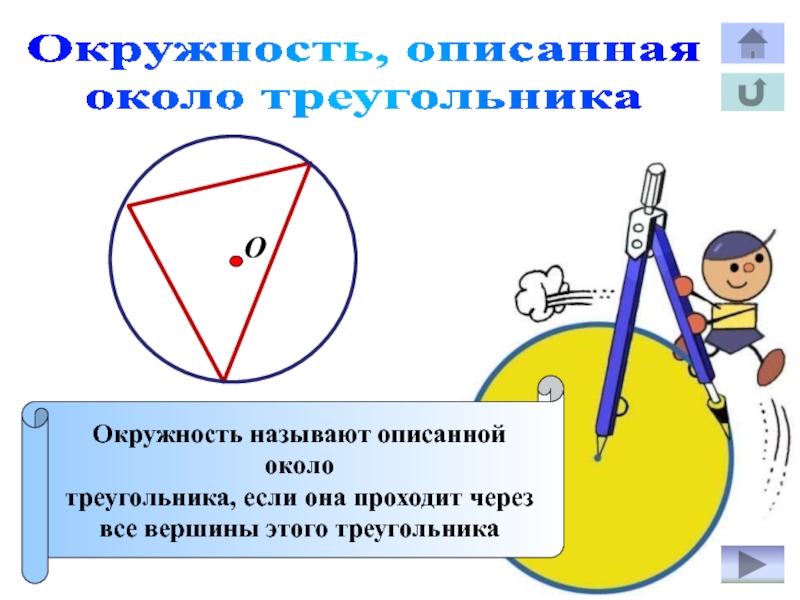
Слайд 17Окружность, описанная
около треугольника
О
Окружность называют описанной около
треугольника, если она проходит
через
все вершины этого треугольника
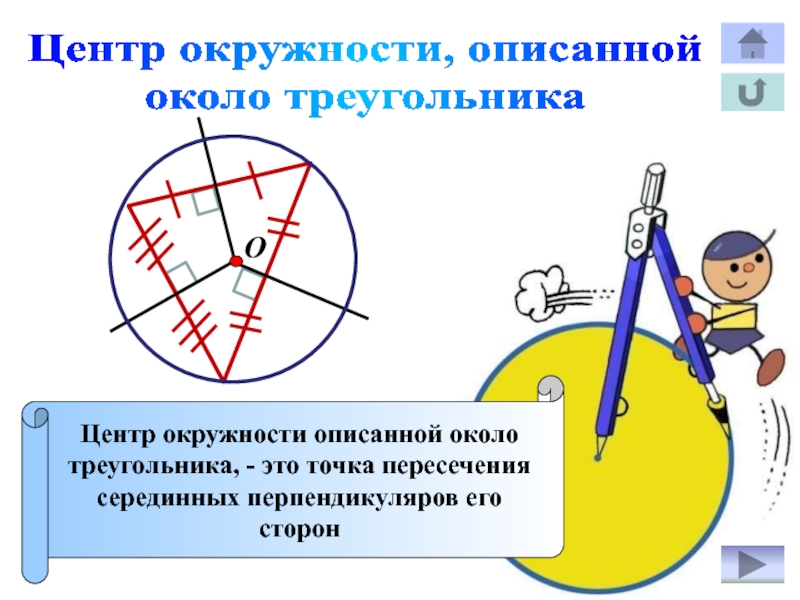
Слайд 18Центр окружности, описанной
около треугольника
О
Центр окружности описанной около
треугольника, - это
точка пересечения
серединных перпендикуляров его сторон
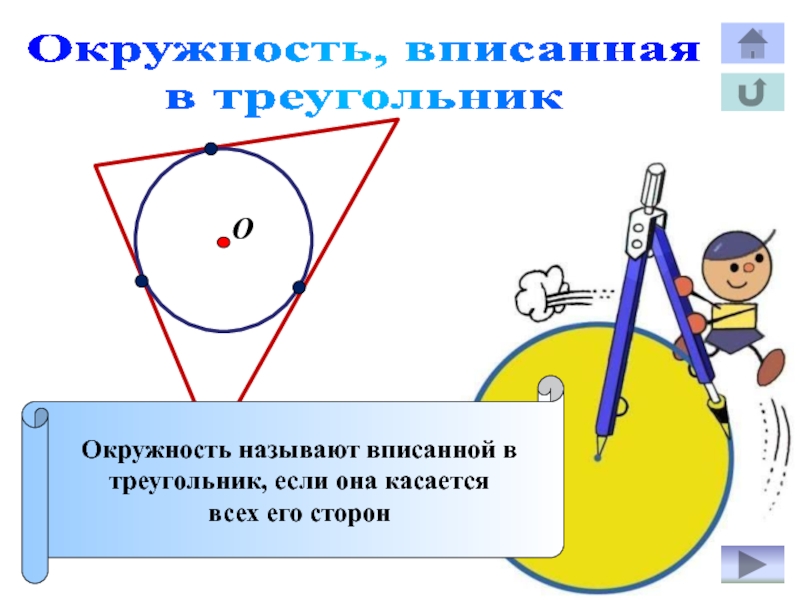
Слайд 19Окружность, вписанная
в треугольник
О
Окружность называют вписанной в
треугольник, если она касается
всех
его сторон
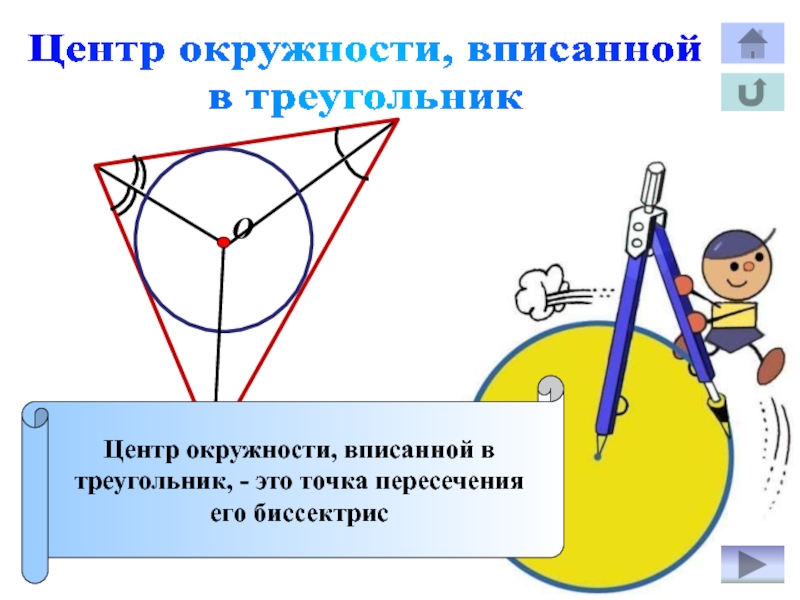
Слайд 20Центр окружности, вписанной
в треугольник
О
Центр окружности, вписанной в
треугольник, - это
точка пересечения
его биссектрис
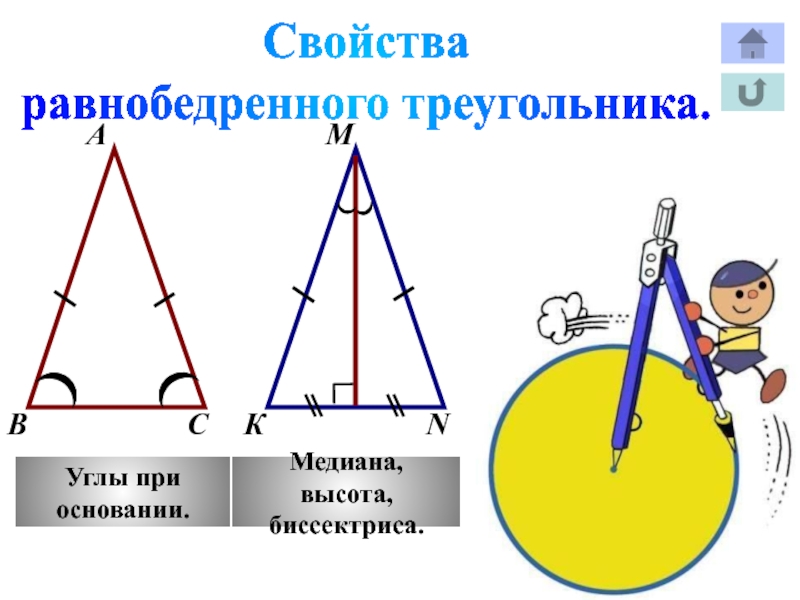
Слайд 25Признаки равенства
прямоугольных треугольников.
А
С
В
КАТЕТ
КАТЕТ
ГИПОТЕНУЗА
По катетам
По катету и гипотенузе
По катету и прилеж.
острому
углу
По гипотенузе
и острому углу
Слайд 27Тестовые задания на
проверку теоретических
знаний.
Необходимо
выбрать правильный ответ.
8
9
1
2
3
4
5
6
7
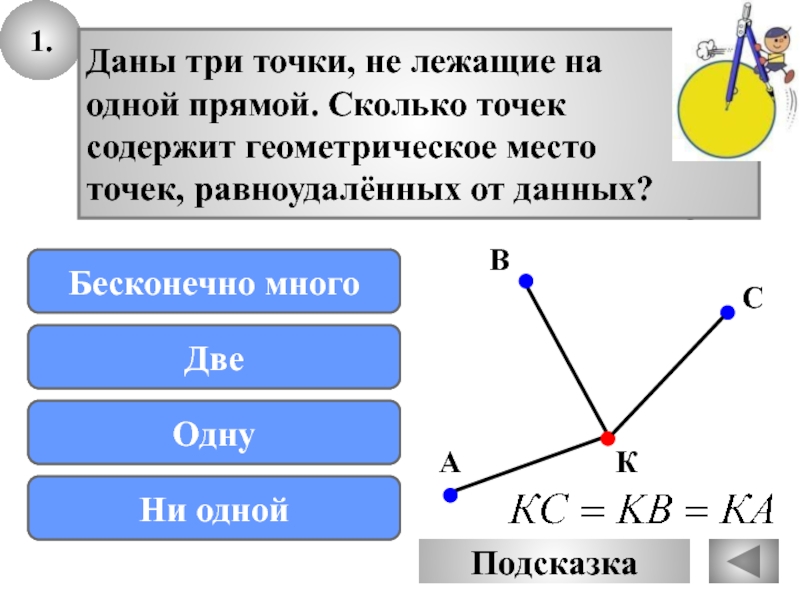
Слайд 281.
В
С
с
А
К
Даны три точки, не лежащие на
одной прямой. Сколько точек
содержит
геометрическое место
точек, равноудалённых от данных?
Подумай!
Бесконечно много
Не верно!
Две
ВЕРНО
Одну
Подумай!
Ни одной
Подсказка
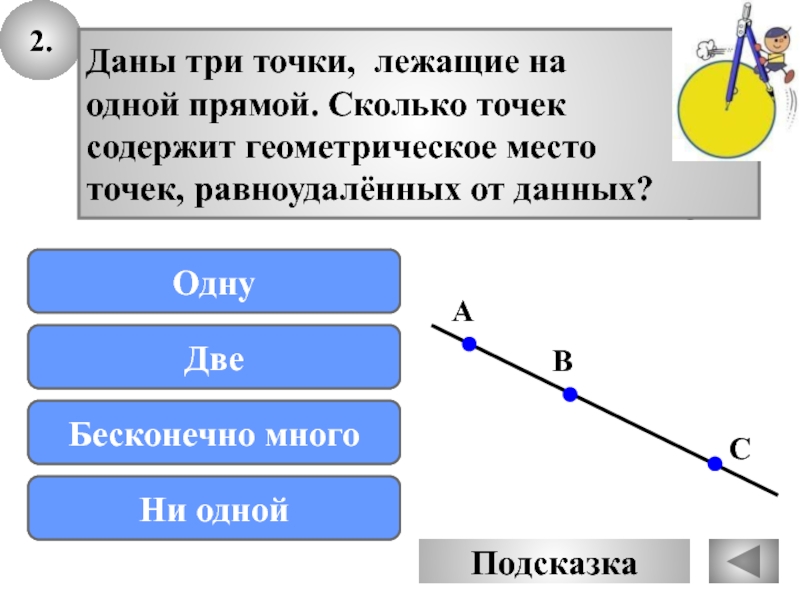
Слайд 292.
В
С
с
А
Даны три точки, лежащие на
одной прямой. Сколько точек
содержит геометрическое
место
точек, равноудалённых от данных?
Подумай!
Бесконечно много
Не верно!
Две
ВЕРНО
Ни одной
Подумай!
Одну
Подсказка
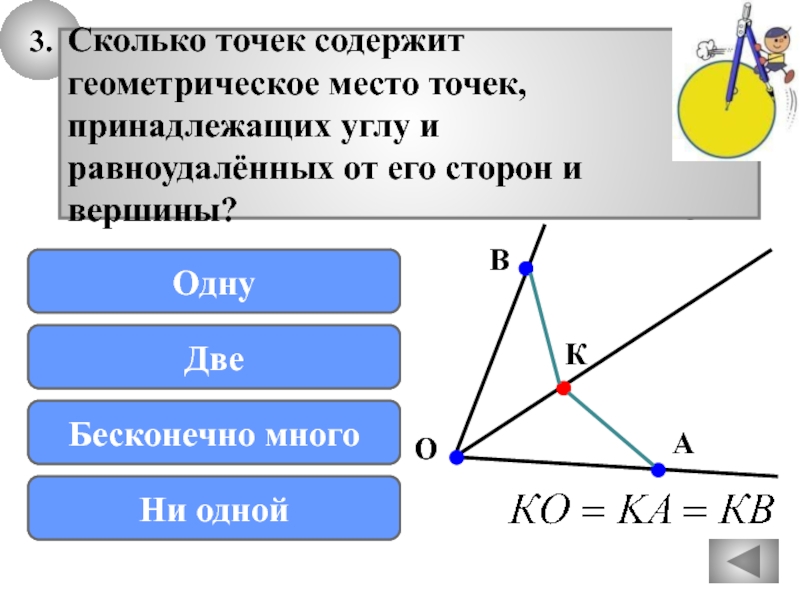
Слайд 303.
В
О
с
А
К
Сколько точек содержит
геометрическое место точек,
принадлежащих углу и
равноудалённых
от его сторон и вершины?
Подумай!
Бесконечно много
Не верно!
Две
ВЕРНО
Одну
Подумай!
Ни одной
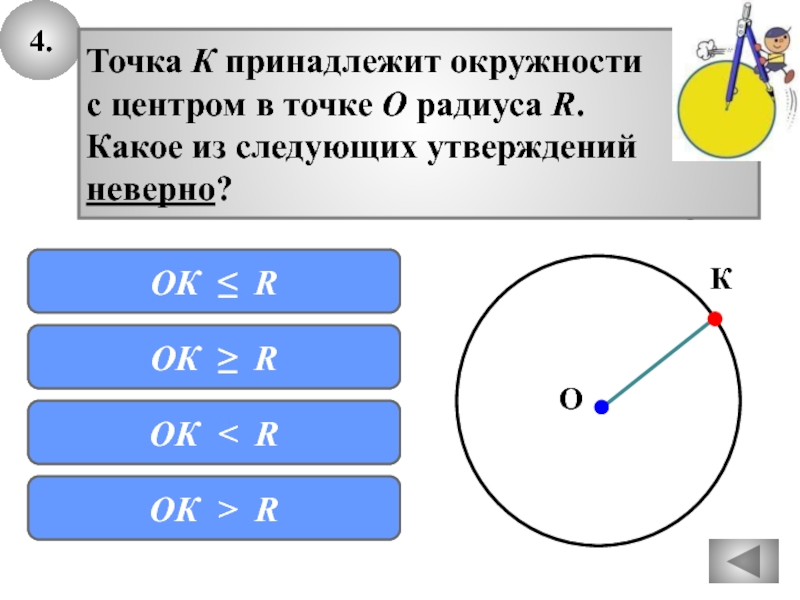
Слайд 314.
с
Точка К принадлежит окружности
с центром в точке О радиуса R.
Какое
из следующих утверждений
неверно?
Подумай!
ОК ≤ R
Подумай!
ОК ≥ R
МОЛОДЕЦ
ОК < R
Подумай!
ОК > R
К
O
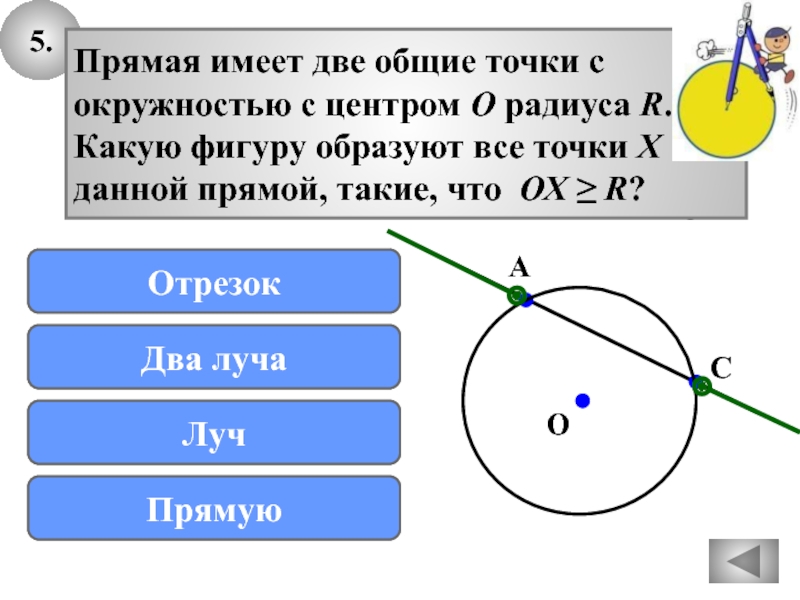
Слайд 325.
О
С
с
А
Прямая имеет две общие точки с
окружностью с центром О радиуса
R.
Какую фигуру образуют все точки Х
данной прямой, такие, что ОХ
≥ R?Подумай!
Луч
Не верно!
Прямую
ВЕРНО
Два луча
Подумай!
Отрезок
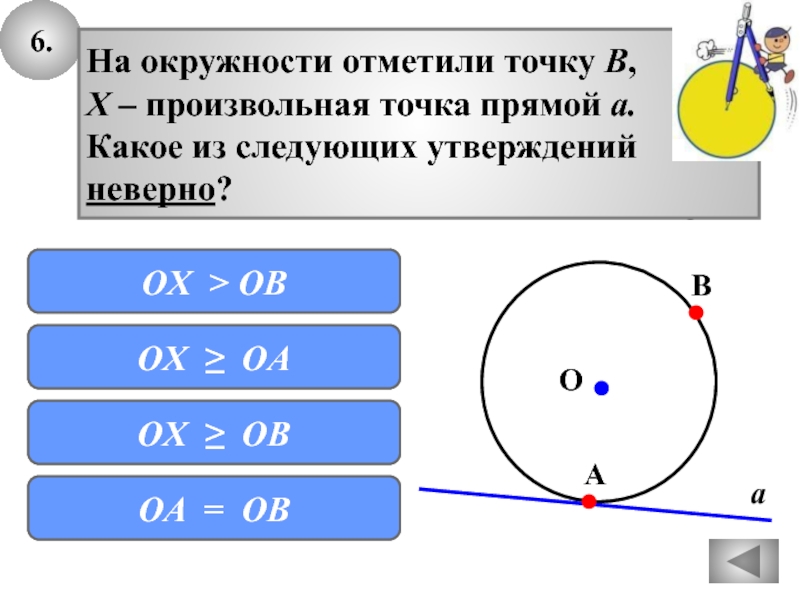
Слайд 336.
с
На окружности отметили точку В,
Х – произвольная точка прямой а.
Какое
из следующих утверждений
неверно?
Подумай!
ОX ≥ OB
Подумай!
ОX ≥ OA
МОЛОДЕЦ
ОX > OB
Подумай!
ОA = OB
В
O
A
a
Слайд 347.
Какое утверждение верно?
Подумай!
Если две хорды перпендикулярны,
то
одна из них является диаметром
Не верно!
Если две хорды точкой пересечения
делятся пополам, то они перпендикулярны
ВЕРНО
Если касательная, проведённая через конец хорды, перпендикулярна ей, то это - диаметр
Подумай!
Если одна из хорд делит другую пополам, то эта хорда - диаметр
Слайд 398.
Центр описанной окружности
треугольника – это точка
пересечения…
Подумай!
Высот треугольника
Подумай!
Медиан
треугольника
МОЛОДЕЦ
Серединных перпендикуляров сторон тр-ка
Подумай!
Биссектрис тр-ка
А
O
Проверка
В
С
Слайд 409.
Центр вписанной окружности
треугольника – это точка
пересечения…
Подумай!
Высот треугольника
Подумай!
Медиан
треугольника
МОЛОДЕЦ
Биссектрис тр-ка
Подумай!
Серединных перпендикуляров сторон тр-ка
А
O
Проверка
В
С
Слайд 4614.
Дан отрезок АВ длиной 3 см. Найдите
ГМТ, равноудалённых от точек
А
и В и находящихся в 2-х см от АВ
Ответ
Построение (4)
O
А
В
2
Подсказка
Признаки
равенствапрямоугольных
треугольников
2
ГМТ – серединный
перпендикуляр
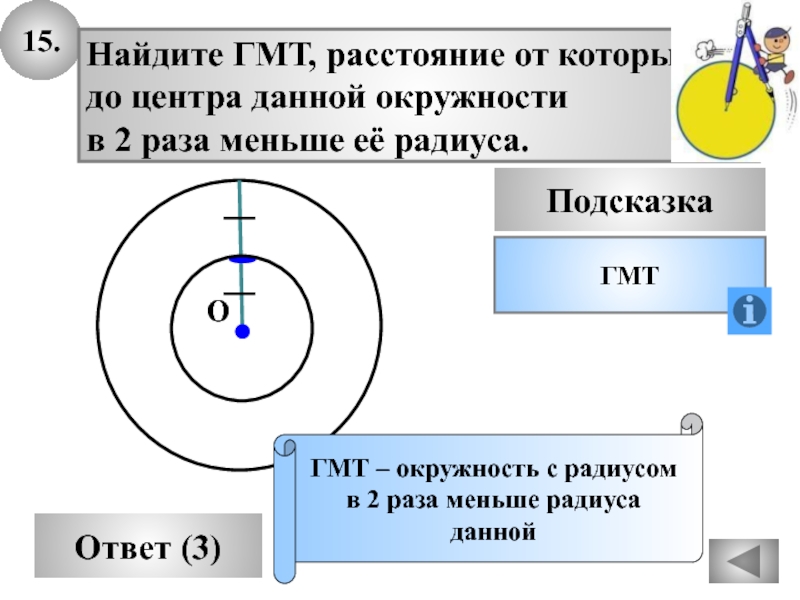
Слайд 4715.
Ответ (3)
Подсказка
ГМТ
Найдите ГМТ, расстояние от которых
до центра данной окружности
в
2 раза меньше её радиуса.
O
ГМТ – окружность с радиусом
в 2
раза меньше радиусаданной
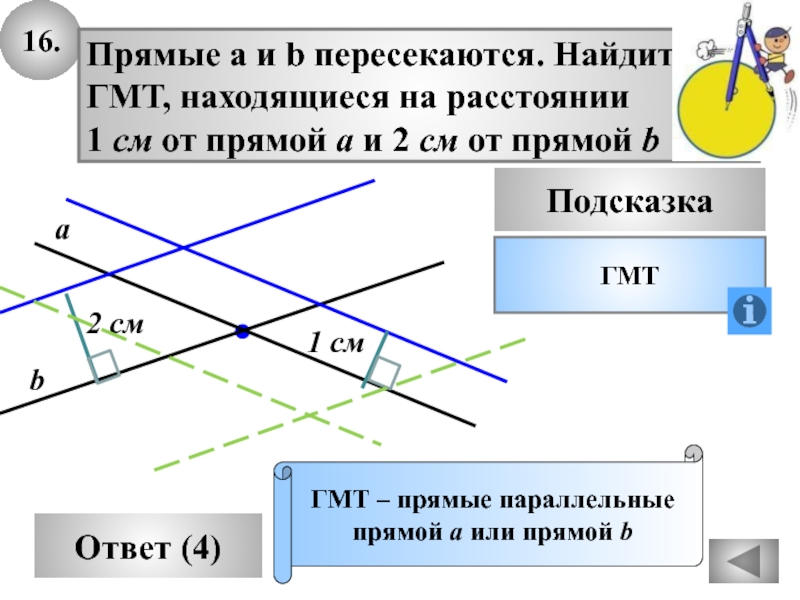
Слайд 4816.
Ответ (4)
Подсказка
ГМТ
Прямые а и b пересекаются. Найдите
ГМТ, находящиеся на расстоянии
1 см от прямой а и 2 см от прямой
bb
a
ГМТ – прямые параллельные
прямой а или прямой b
1 cм
2 cм
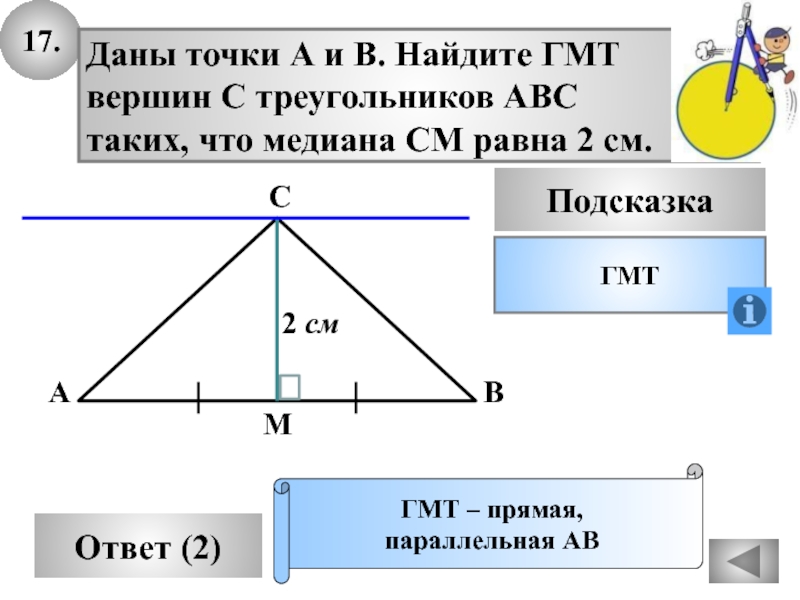
Слайд 4917.
Ответ (2)
Подсказка
ГМТ
Даны точки А и В. Найдите ГМТ
вершин С треугольников
АВС
таких, что медиана СМ равна 2 см.
ГМТ – прямая,
параллельная АВ
В
А
С
2 см
М
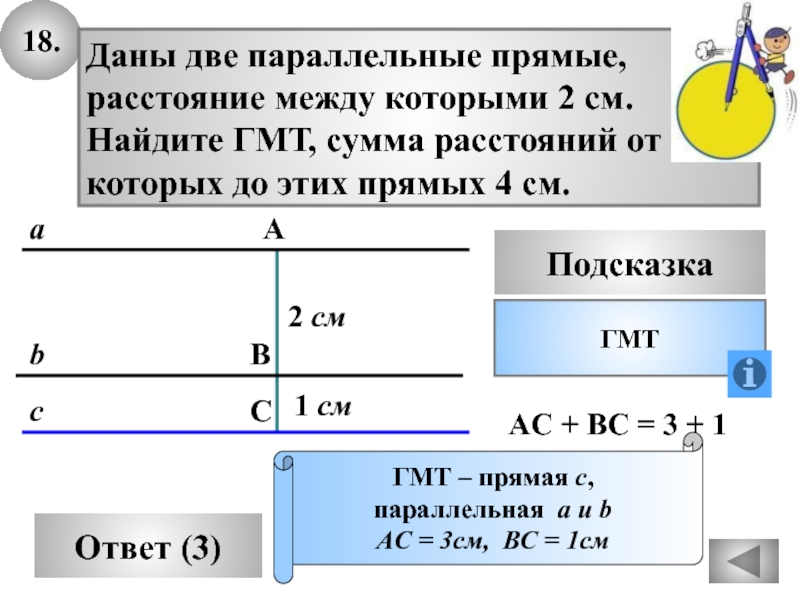
Слайд 5018.
Ответ (3)
Подсказка
ГМТ
Даны две параллельные прямые,
расстояние между которыми 2 см.
Найдите ГМТ,
сумма расстояний от
которых до этих прямых 4 см.
ГМТ – прямая
c, параллельная a и b
АС = 3см, ВС = 1см
b
c
а
2 см
A
B
C
AC + ВC = 3 + 1
1 см
Слайд 5219.
Ответ
Подсказка
Равенство
прямоуг. тр-ов
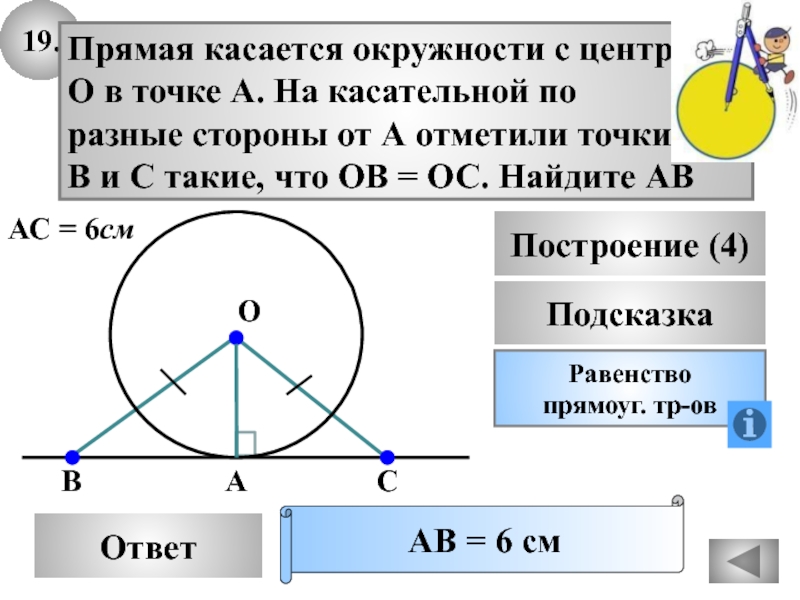
Прямая касается окружности с центром
О в точке А. На
касательной по
разные стороны от А отметили точки
В и С такие,
что ОВ = ОС. Найдите АВАВ = 6 см
АС = 6см
О
B
С
Построение (4)
А
Слайд 53Равнобедренный
треугольник
20.
Ответ
Подсказка (3)
Определить угол
ОВА
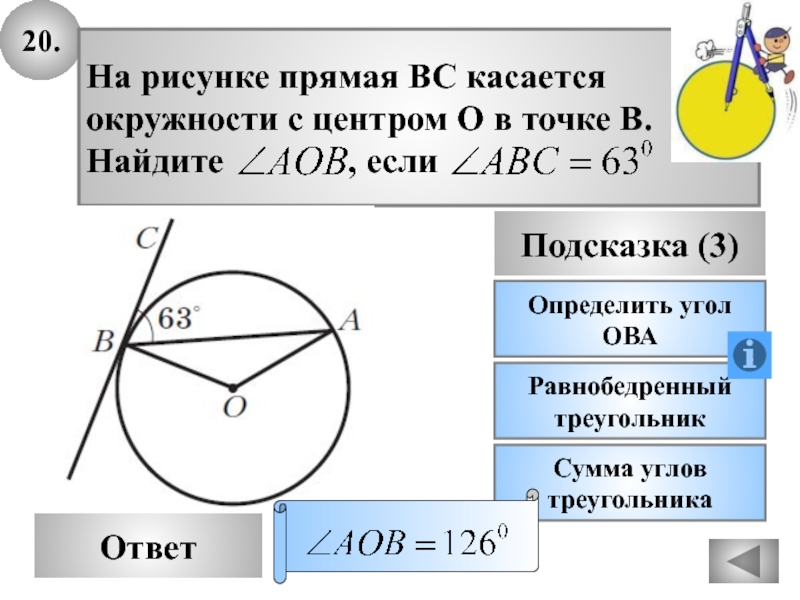
На рисунке прямая ВС касается
окружности с центром О
в точке В.
Найдите ,
если Сумма углов
треугольника
Слайд 5421.
Ответ
Подсказка
Выполнить
дополнительное
построение
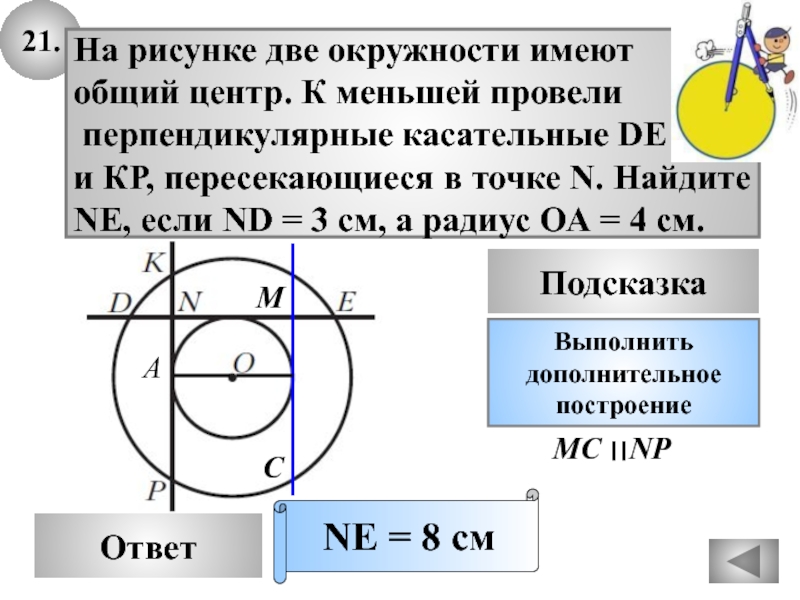
На рисунке две окружности имеют
общий центр. К меньшей
провели
перпендикулярные касательные DE
и КР, пересекающиеся в точке N. Найдите
NE,
если ND = 3 см, а радиус ОА = 4 см.NE = 8 см
А
М
С
МС ׀׀NP
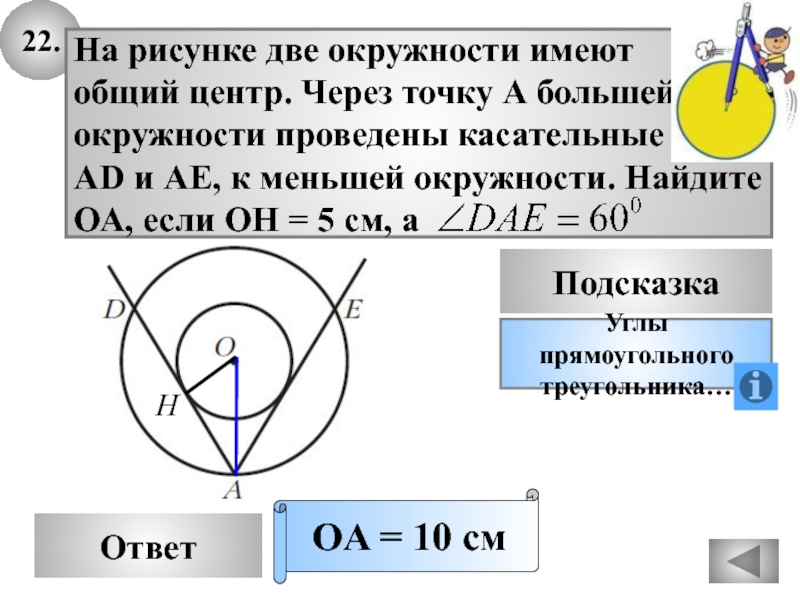
Слайд 5522.
Ответ
На рисунке две окружности имеют
общий центр. Через точку А большей
окружности
проведены касательные
АD и АЕ, к меньшей окружности. Найдите
ОА, если ОН
= 5 см, а OA = 10 см
H
Подсказка
Углы прямоугольного
треугольника…
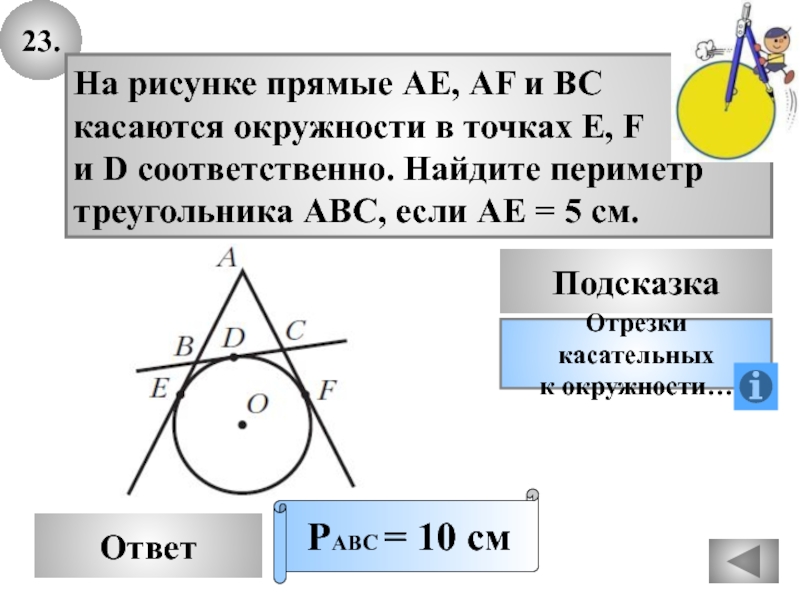
Слайд 5623.
Ответ
На рисунке прямые АЕ, AF и ВС
касаются окружности в точках
E, F
и D соответственно. Найдите периметр
треугольника АВС, если АЕ
= 5 см.РАВС = 10 см
Подсказка
Отрезки касательных
к окружности…
Слайд 58Равнобедренный
треугольник…
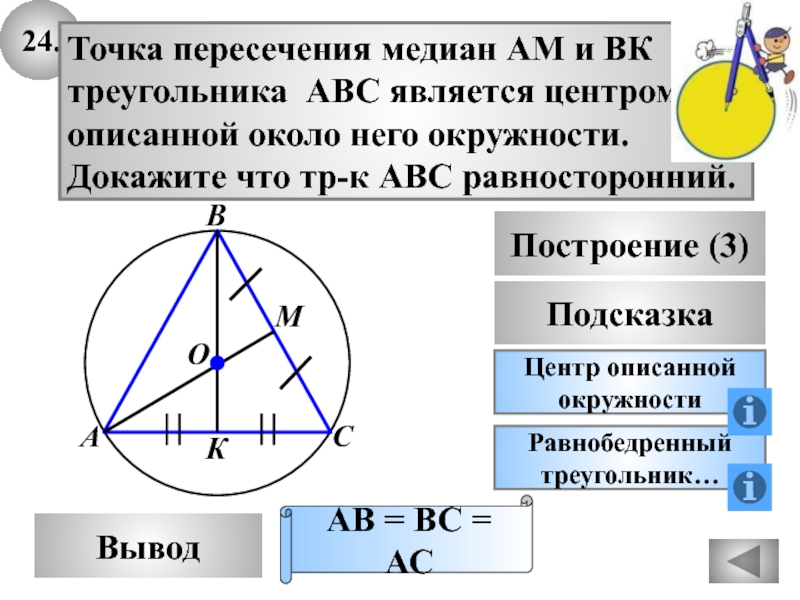
24.
Вывод
Подсказка
Центр описанной
окружности
Точка пересечения медиан АМ и ВК
треугольника АВС является центром
описанной
около него окружности.
Докажите что тр-к АВС равносторонний.
АВ = ВС
= АСПостроение (3)
А
В
С
М
К
О
Слайд 59Равнобедренный
треугольник…
25.
Вывод
Подсказка (2)
Центр описанной
окружности
На серединном перпендикуляре стороны
АВ треугольника АВС отмечена
точка О
так, что
. Докажите что точка О – центр окружности описанной
около треугольника АВС.
О – центр описанной окр-ти
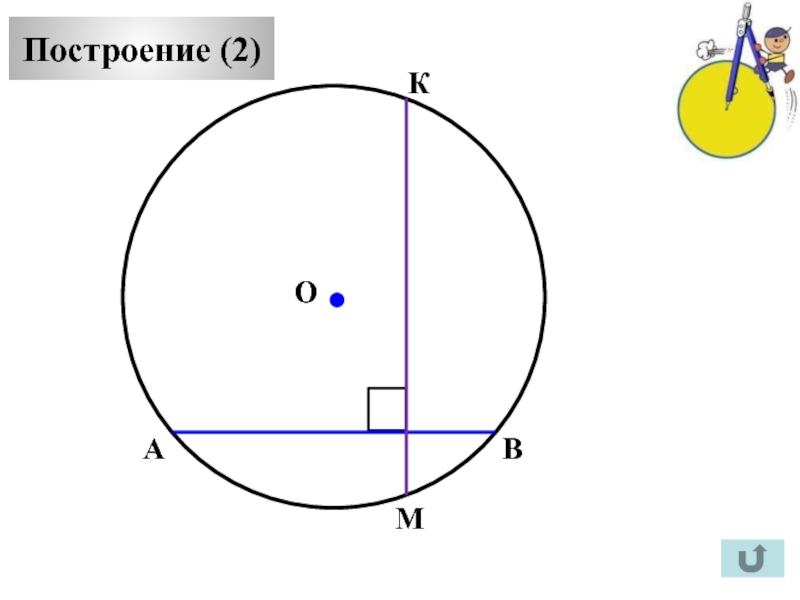
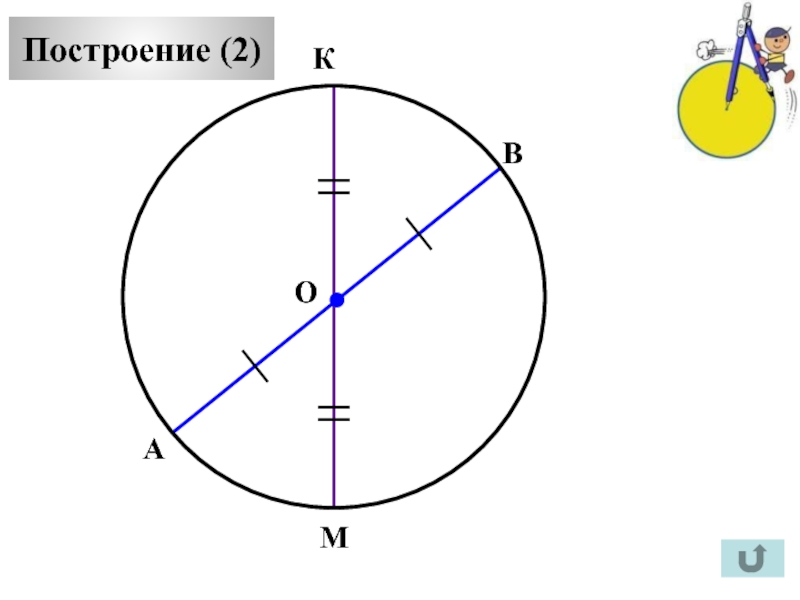
Построение (2)
А
С
В
М
К
О
Слайд 60Равнобедренный
треугольник…
26.
Вывод
Подсказка (2)
Центр вписанной
окружности
Найдите высоту равностороннего
треугольника, если радиус окр-ти,
вписанной в этот
треугольник, равен
8 см
ВН = 24 см
Построение (3)
А
С
В
К
Н
О
Слайд 61Отрезки касательных
к окружности
27.
Вывод
Подсказка (2)
Вписанная
окружность
Боковая сторона равнобедренного тр-ка
делится точкой касания вписанной
окр-ти
в отношении 3 : 4, считая от вершины при
основании. Найти боковую сторону тр-ка,
если его основание 12см.
ВС = 14 см
Построение (3)
А
С
В
К
3
О
4
Р
Т
Слайд 62Отрезки касательных
к окружности
28.
Вывод
Подсказка
В прямоугольном треугольнике точка
касания вписанной окружности делит
гипотенузу на
отрезки 4 см и 6 см. Найдите
периметр треугольника, если радиус
окр-ти 2 смРАВС = 24 см
Построение (2)
А
С
В
К
4
О
6
Р
Т
Слайд 63Отрезки касательных
к окружности
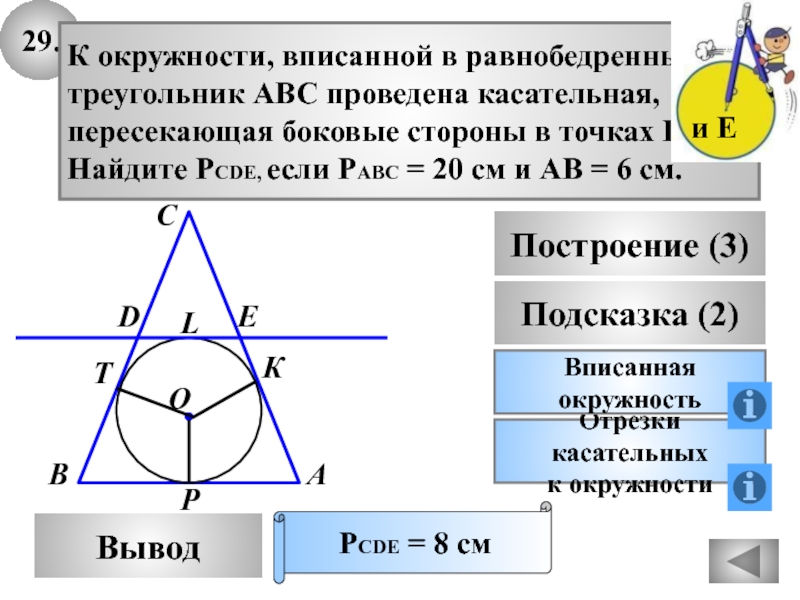
29.
Вывод
Подсказка (2)
Вписанная
окружность
К окружности, вписанной в равнобедренный
треугольник АВС проведена
касательная,
пересекающая боковые стороны в точках D
Найдите PCDE, если
РАВС = 20 см и АВ = 6 см.PCDE = 8 см
Построение (3)
А
С
В
К
О
Р
Т
и Е
D
E
L
Слайд 64Отрезки касательных
к окружности
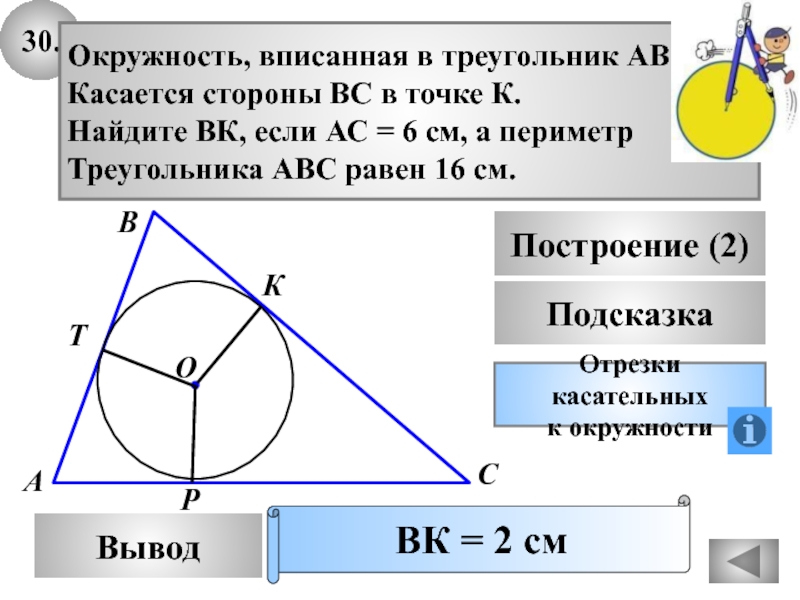
30.
Подсказка
Окружность, вписанная в треугольник АВС,
Касается стороны ВС в
точке К.
Найдите ВК, если АС = 6 см, а
периметрТреугольника АВС равен 16 см.
ВК = 2 см
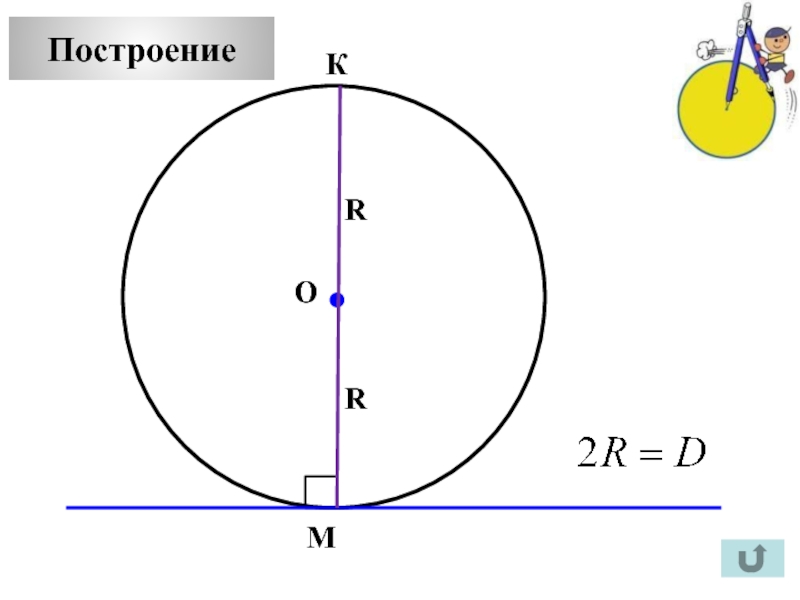
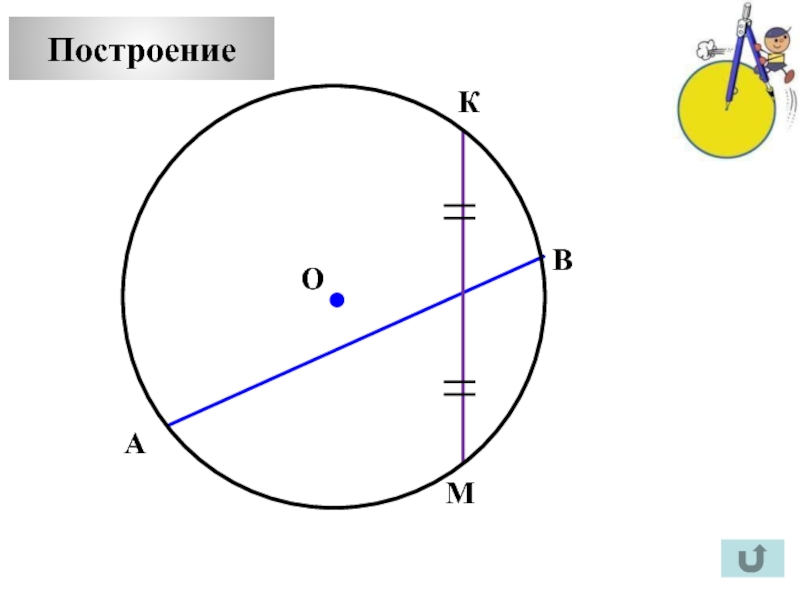
Построение (2)
А
С
В
К
О
Р
Т
Вывод
Слайд 65Используемые ресурсы:
4. «Геометрия 7»: Учеб. для учащихся общеобразовательных. организаций/
А.Г.Мерзляк, В.Б.Полонский, М.С.Якир
М.: Вента Граф 2016
1.
Картинка: http://do2.rcokoit.ru/pluginfile.php/504972/mod_page/content/11/013.jpg
2. Глаз
http://clipart-library.com/data_images/21486.png
3. Геометрия: дидактические материалы: 7класс: пособиедля учащихся общеобразовательных. организаций/
А.Г.Мерзляк, В.Б.Полонский, М.С.Якир
М.: Вента Граф 2017