Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия и симметричные фигуры
Содержание
- 1. Симметрия и симметричные фигуры
- 2. План урока1) Центральная симметрия2) Осевая симметрия3) Зеркальная
- 3. Центральная симметрия Две точки А и
- 4. Фигура называется симметричной относительно точки О, если
- 5. Осевая симметрия Две точки
- 6. Фигура называется симметричной относительно прямой а, если
- 7. Прямоугольник и ромб, не являющиеся квадратами имеют
- 8. Имеются фигуры, у которых нет ни одной
- 9. Зеркальная симметрияЧто может быть больше похоже на
- 10. Зеркально симметричные объектыОсевая симметрияЗеркальная симметрияЦентральная симметрия
- 11. Возьмем зеркало, поставим его вертикально так ,
- 12. Зеркало не подействовало на слово « КОФЕ»
- 13. Поворотная симметрияПоворотная симметрия - это такая симметрия
- 14. Слайд 14
- 15. Симметрия вокруг насМногие листья деревьев и лепестки
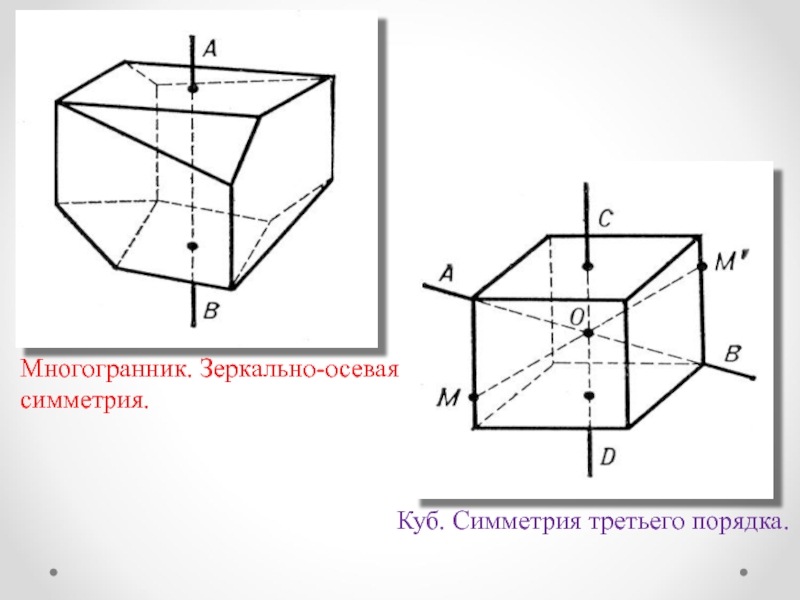
- 16. Многогранник. Зеркально-осевая симметрия.Куб. Симметрия третьего порядка.
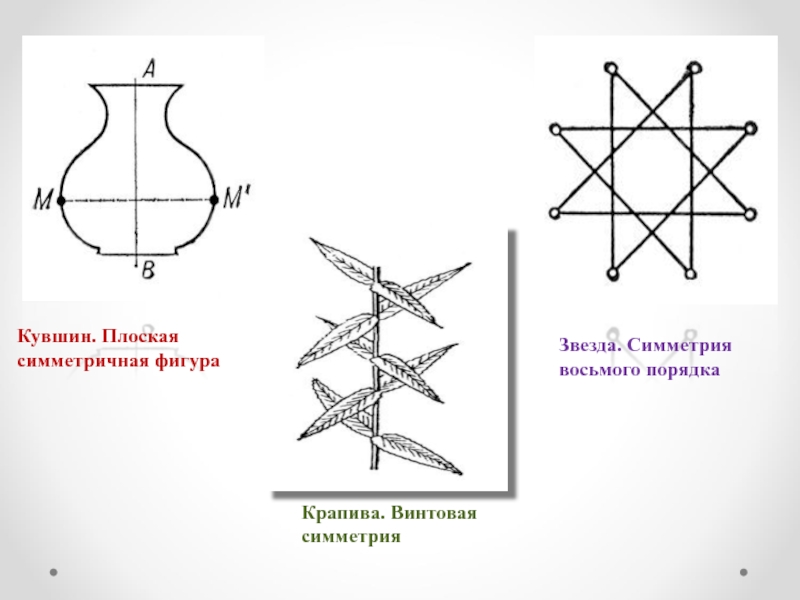
- 17. Кувшин. Плоская симметричная фигураКрапива. Винтовая симметрияЗвезда. Симметрия восьмого порядка
- 18. Зеркальная симметрия в природе
- 19. Симметрия в архитектуре
- 20. Слайд 20
- 21. Симметрия в искусстве
- 22. Симметрия в технике
- 23. Симметрия в природе
- 24. Спасибо за внимание и урок!
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2План урока
1) Центральная симметрия
2) Осевая симметрия
3) Зеркальная симметрия
4) Поворотная симметрия
5)
Симметрия в природе и геометрии
Слайд 3Центральная симметрия
Две точки А и А1 называются симметричными
относительно точки О, если О - середина отрезка АА1. Точка
О считается симметричной самой себе.На рисунке точки М и М1, N и N1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.
Центральная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно центра О.
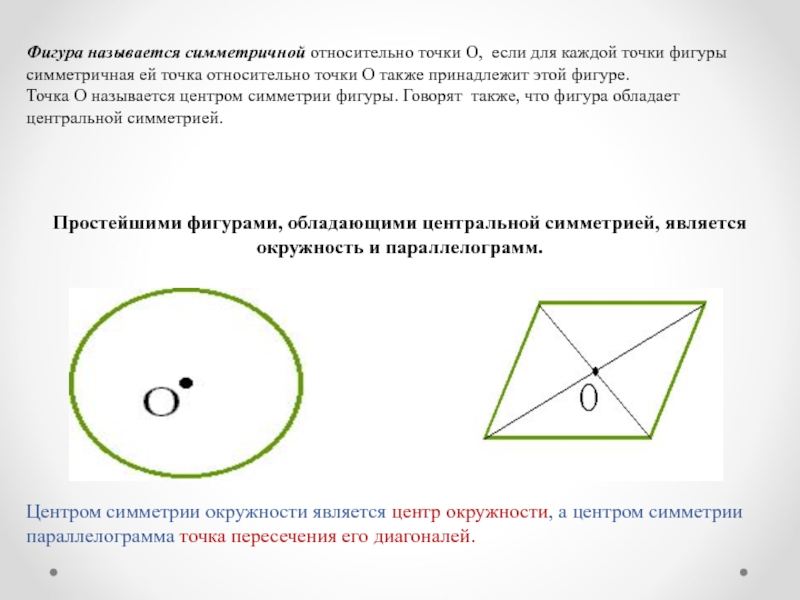
Слайд 4Фигура называется симметричной относительно точки О, если для каждой точки
фигуры симметричная ей точка относительно точки О также принадлежит этой
фигуре.Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма точка пересечения его диагоналей.
Слайд 5Осевая симметрия
Две точки А и А1
называются симметричными относительно прямой а, если эта прямая проходит через
середину отрезка АА1 и перпендикулярна к нему.Каждая точка прямой а считается симметричной самой себе.
Осевая симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно оси а.
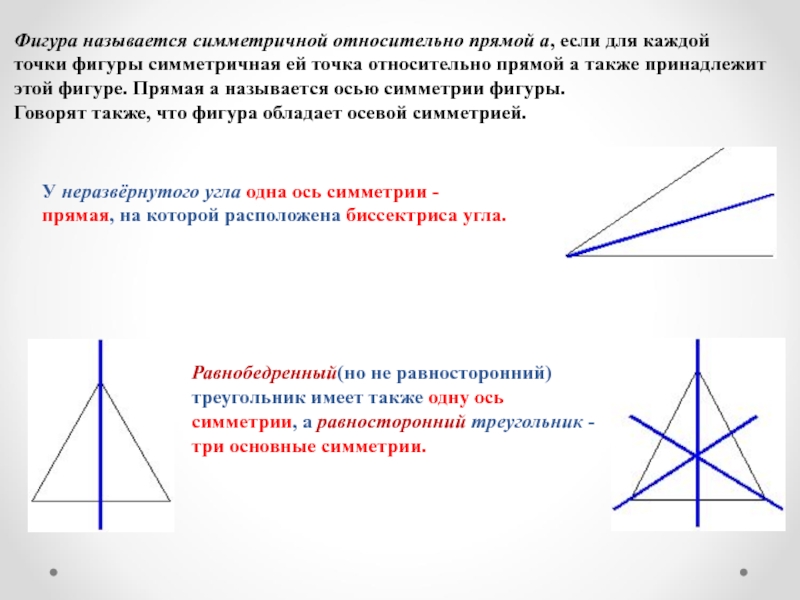
Слайд 6Фигура называется симметричной относительно прямой а, если для каждой точки
фигуры симметричная ей точка относительно прямой а также принадлежит этой
фигуре. Прямая а называется осью симметрии фигуры.Говорят также, что фигура обладает осевой симметрией.
У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла.
Равнобедренный(но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник - три основные симметрии.
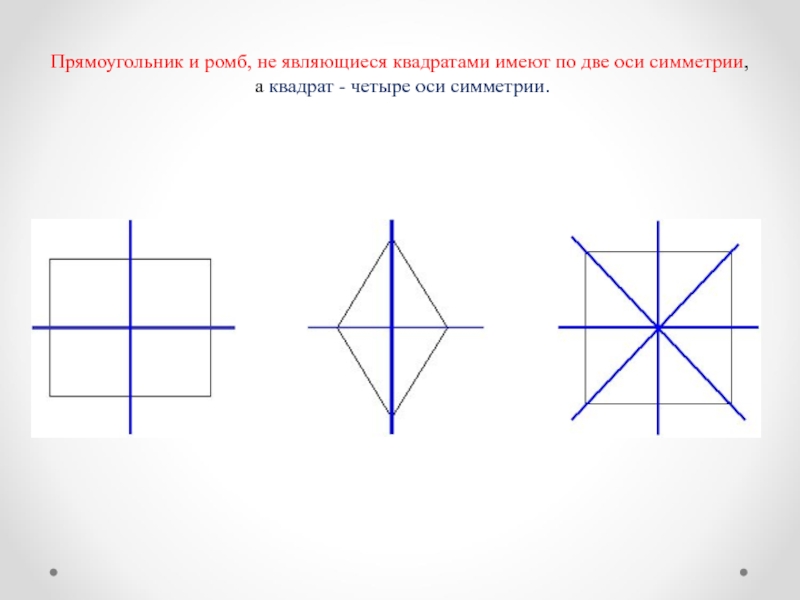
Слайд 7Прямоугольник и ромб, не являющиеся квадратами имеют по две оси
симметрии,
а квадрат - четыре оси симметрии.
Слайд 8
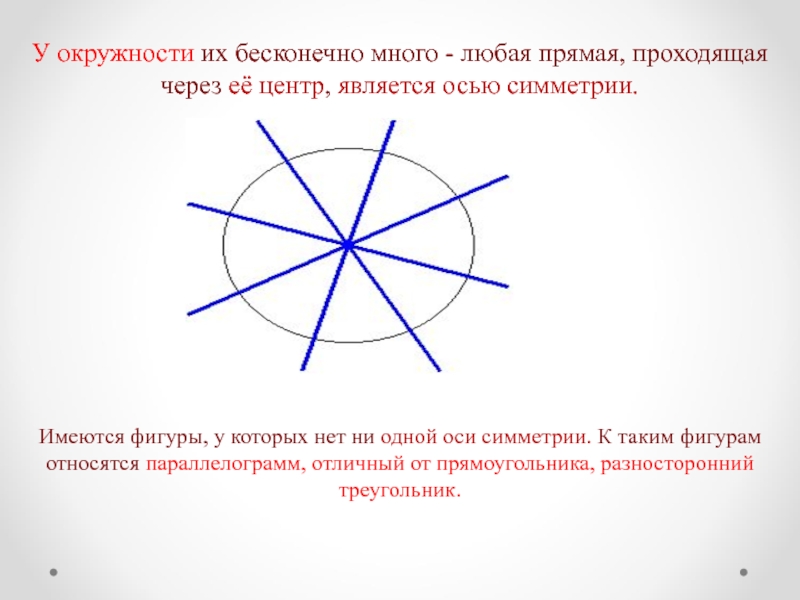
Имеются фигуры, у которых нет ни одной оси симметрии. К
таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
У окружности
их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.Слайд 9Зеркальная симметрия
Что может быть больше похоже на мою руку или
мое ухо , чем их собственное отражение в зеркале ?
И все же руку которую я вижу в зеркале , нельзя поставить на место настоящей руки.(Иммануил Кант )
Зеркальная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости а.
Слайд 11Возьмем зеркало, поставим его вертикально так , чтобы линия пересечения
плоскости зеркала с плоскостью листа, на котором написано два слова
«ЧАЙ» и «КОФЕ» делила эти слова по горизонтали . Какое слово изменится и почему?Игра с зеркалом
Слайд 12Зеркало не подействовало на слово « КОФЕ» , тогда как
слово «ЧАЙ» оно изменило до неузнаваемости . Этот фокус имеет
простое объяснение . Разумеется , зеркало одинаковым образом отражает нижнюю половину обеих слов . Однако в отличии от слова «ЧАЙ» слово«КОФЕ» обладает горизонтальной осью симметрии , именно поэтому оно не искажается при отражении в зеркале .
Слайд 13Поворотная симметрия
Поворотная симметрия - это такая симметрия при которой объект
совмещается сам с собой при повороте вокруг некоторой оси на
угол, равный 360°/n, где n = 2,3,4...Слайд 15Симметрия вокруг нас
Многие листья деревьев и лепестки цветов симметричны относительно
среднего стебля. С симметрией мы часто встречаемся в искусстве; архитектуре;
технике; быту. Так, фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях.Симметрия переноса
Симметрия. Орнамент