Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления
Содержание
- 1. Системы счисления
- 2. Числа не управляют миром, но показывают, как управляется мирИоганн Гете
- 3. Медвежонок Винни мечтал стать таким же умным.как
- 4. Ей было 1100 лет.Она в 101 класс
- 5. Счет появился тогда, когда человеку потребовалось
- 6. Арифметические знания требовались, чтобы:с успехом заниматься
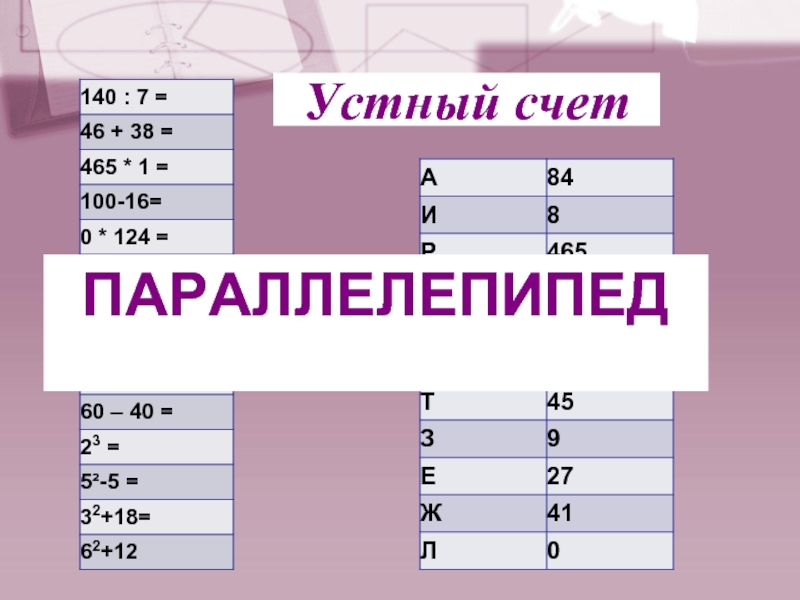
- 7. Слайд 7
- 8. Египетская нумерацияЕгиптяне придумали эту систему около 5 000
- 9. Древняя греческая нумерацияВ ней числа 1 - 9 обозначаются
- 10. В древнем Вавилоне примерно за 40 веков
- 11. Нумерация индейцев Майя123456789101112131520 или 0 Сначала эта
- 12. Китайская нумерацияВозникла эта нумерация около 4 000
- 13. Славянская кириллическая нумерацияЭта нумерация была создана вместе
- 14. Это, наверное, самая известная нумерация, после арабской.
- 15. Арабская нумерацияЭто, самая распространенная на сегодняшний
- 16. Дружно с вами мы считали и про
- 17. Системы счисленияПозиционные(значение цифр зависит от позиции в числе)Непозиционные(значение цифр не зависит от позиции в числе)
- 18. Основные недостатки непозиционных систем:Запись больших чисел требует
- 19. Позиционные системы Как указать принадлежность
- 20. 24110=1111000125010=1100102двоичная система счисления2-основание0,1-алфавит10012=1*23+0*22+0*21+1*20=
- 21. троичная система счисления3-основание0,1,2-алфавитПеревод из 3-ичной системы в
- 22. двенадцатеричная система счисления12-основание0,1,2,3,4,5,6,7,8,9,A,B-алфавитЧисло двенадцать (дюжина) даже составляла
- 23. десятеричная система счисления10-основание0,1,2,3,4,5,6,7,8,9-алфавит«Преимущество десятичной системы не математическое,
- 24. Соответствие первых двух десятков двоичной и десятичной
- 25. рефлексия Подошёл к концу наш урок. Давайте
- 26. Литература, ресурсы интернетО. М Шаров. Н. А.
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1системы счисления
Методическая разработка учителя математики МОУ Коляновская СОШ,
Ивановского района, Ивановской
области Опалевой ОА
Слайд 3Медвежонок Винни мечтал
стать таким же умным.
как его знакомая сова.
Поэтому он решил изучить
все книги, какие только
есть на
свете. Прочитав стихотворение
А.Н.Старикова,
медвежонка поразила
совершенно невероятная
…девочка.
Слайд 4Ей было 1100 лет.
Она в 101 класс ходила.
В портфеле по
100 книг носила.
Всё это правда, а не бред.
Когда, пыля десятком
ног,Она шагала по дороге За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И 10 загорелых рук
Портфель и поводок держали.
И 10 тёмно-синих глаз
Оглядывали мир привычно.
Но станет всё совсем обычным,
Когда поймёте наш рассказ.
Винни решил во всём разобраться, конечно, не без помощи мудрой совы.
Как такое может быть!
Откуда взялись такие числа?
Откуда, вообще, взялись числа?
Слайд 5 Счет появился тогда, когда человеку потребовалось информировать
своих сородичей
о количестве обнаруженных им предметов.
Самая простая система счисления была
у древних людей.Какое число нужно записать, столько сделают засечек на палке, или в кучку камешков положат.
Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?
Слайд 6
Арифметические знания требовались, чтобы:
с успехом заниматься сельским хозяйством
строить здания, дворцы,
дамбы, пирамиды…
совершать далёкие путешествия
вести торговые дела
вычислять и предугадывать наперёд пути
движения планет на небеВ разных уголках планеты складывались свои системы счисления
Слайд 8Египетская нумерация
Египтяне придумали эту систему около 5 000 лет тому назад
Записывались цифры числа начиная с больших значений и заканчивая меньшими.
Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
Например:
1
10
100
1000
10000
100000
1000000
10000000
135
13209
Слайд 9Древняя греческая нумерация
В ней числа 1 - 9 обозначаются первыми буквами греческого
алфавита:
числа 10, 20, … 90:
числа 100, 200, … 900 последними
девятью буквами:Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами.
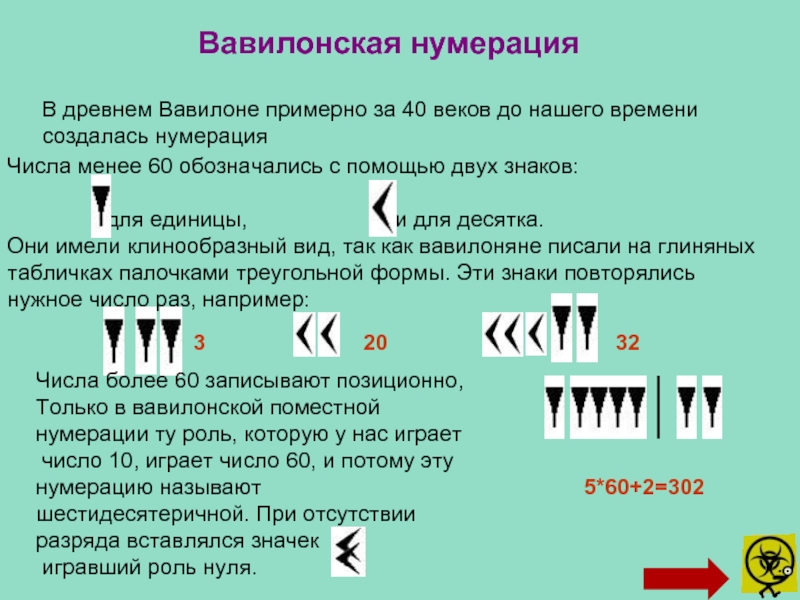
Слайд 10В древнем Вавилоне примерно за 40 веков до нашего времени
создалась нумерация
Вавилонская нумерация
Числа менее 60 обозначались с помощью двух знаков:
для единицы, и для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например:
3
20
32
5*60+2=302
Числа более 60 записывают позиционно,
Только в вавилонской поместной
нумерации ту роль, которую у нас играет
число 10, играет число 60, и потому эту
нумерацию называют шестидесятеричной. При отсутствии разряда вставлялся значек
игравший роль нуля.
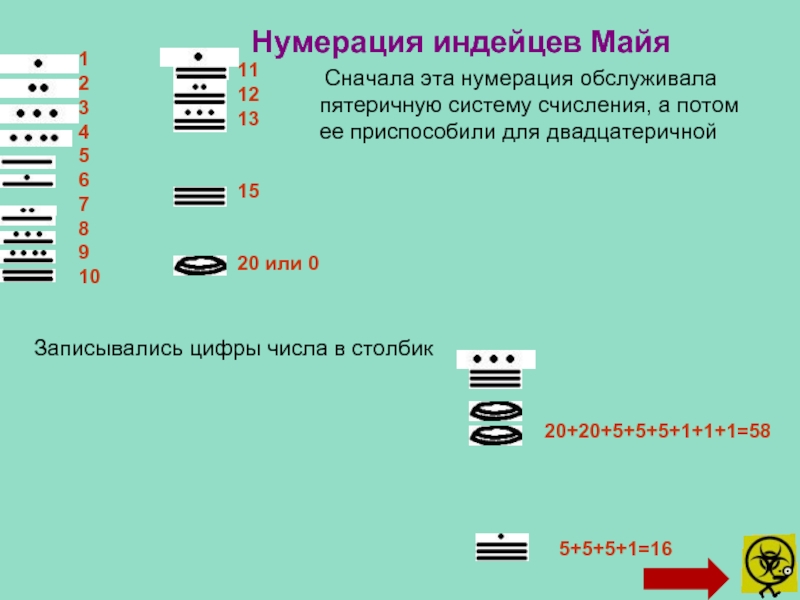
Слайд 11Нумерация индейцев Майя
1
2
3
4
5
6
7
8
9
10
11
12
13
15
20 или 0
Сначала эта нумерация обслуживала
пятеричную систему
счисления, а потом
ее приспособили для двадцатеричной
Записывались цифры числа
в столбик 20+20+5+5+5+1+1+1=58
5+5+5+1=16
Слайд 12Китайская нумерация
Возникла эта нумерация около 4 000 тысяч лет тому
назад в Китае.
°
1
2
3
4
5
6
7
8
9
0
Записывались цифры числа начиная с больших значений
и заканчивая меньшими.Например
10 100 1000
2*1000=2 000
5*100+4*10+6=546
Слайд 13Славянская кириллическая нумерация
Эта нумерация была создана вместе со славянской алфавитной
системой для переписки священных книг для славян греческими монахами братьями
Кириллом (Константином) и Мефодием в IX веке.Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали
Для того, чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения больших, чем 900 чисел использовались специальные значки, добавляемые к букве.
В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая «арабская нумерация».
Слайд 14Это, наверное, самая известная нумерация, после арабской. С нею мы
достаточно часто сталкиваемся в повседневной жизни. Это номера глав в
книгах, указание века, числа на циферблате часов, и т. д.Возникла эта нумерация в древнем Риме.
Латинская (Римская) нумерация
Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание.
CCXXXVII = 100+100+10+10+10+5+1+1 = 237
XXXIX = 10+10+10-1+10 = 39
Есть правило, по которому нельзя записывать подряд 4 одинаковых цифры, такая комбинация заменяется комбинацией с правилом вычитания, например:
XXXX = XC (50-10)
IIII = IV (5-1)
CCCC = CD (500-100)
Слайд 15 Арабская нумерация
Это, самая распространенная на сегодняшний день нумерация. Название
"арабская" для нее не совсем верно, поскольку хоть и завезли
ее в Европу из арабских стран, но там она тоже была не родной. Настоящая родина этой нумерации - Индия.Форма индийских цифр претерпевала многообразные изменения.
Та форма, которой мы сейчас пользуемся установилась в XVI веке
Древнее изображение десятичных цифр не случайно:
каждая цифра обозначает число по количеству углов в ней.
Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д.
Слайд 16Дружно с вами мы считали и про числа рассуждали,
А теперь
мы дружно встали, свои косточки размяли.
На счет раз кулак
сожмем, на счет два в локтях сожмем.На счет три — прижмем к плечам, на 4 — к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем — добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Числа, я, и вы, друзья, вместе дружная 7-я.
физкультминутка
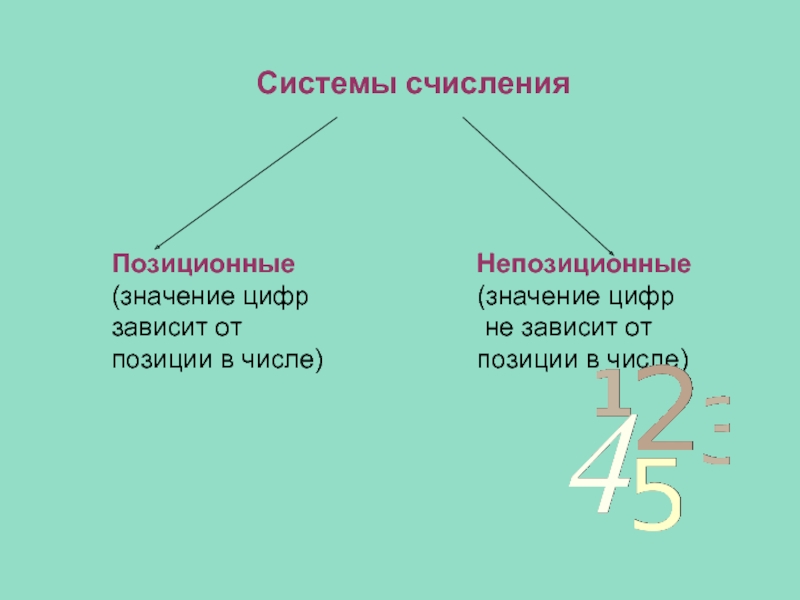
Слайд 17Системы счисления
Позиционные
(значение цифр
зависит от
позиции в числе)
Непозиционные
(значение цифр
не
зависит от
позиции в числе)
Слайд 18Основные недостатки непозиционных систем:
Запись больших чисел требует введения новых символов.
Невозможно
представлять дробные и отрицательные числа.
Сложно выполнять простейшие арифметические операции.
непозиционные системы
Римская
Алфавитные
(Греческая, славянская)Слайд 19Позиционные системы
Как указать принадлежность числа к какой-либо
системе счисления? Основание системы приписывается нижним
индексом
к этому числу. (1123 = 1410 )Основанием позиционной системы счисления может быть
любое число, большее1.
«Мысль выражать все числа немногими знаками,
придавая им, кроме значения по форме,
ещё значение по месту, настолько проста,
что именно из-за этой простоты трудно оценить,
насколько она удивительна»
Франц. математик Пьер Лаплас (1749-1827)
Слайд 2024110=111100012
5010=
1100102
двоичная система счисления
2-основание
0,1-алфавит
10012=1*23+0*22+0*21+1*20=
=1*8+0*4+0*2+1*1=910
50:2=25 0
25:2=12 1
12:2=6
0
6:2=3 0
3:2=1 1
5010=1100102
241 : 2
= 120 1 120 : 2 = 60 0
60 : 2 = 30 0
30 : 2 = 15 0
15 : 2 = 7 1
7 : 2 = 3 1
3 : 2 = 1 1
241 10=111100012
1*24+0*23+1*22+1*21+0*20=
=1*16+0*8+1*4+1*2+0*1=2210
Перевод из 2-ичной системы в 10-ичную
Перевод из 10-ичной системы в 2-ичную
остаток
101102=
Слайд 21троичная система счисления
3-основание
0,1,2-алфавит
Перевод из 3-ичной системы в 10-ичную
12103=1*33+2*32+1*31+0*30=
=1*27+2*9+1*3+0*1=4810
=2*32+0*31+1*30=
=2*9+0*3+1*1=1910
241:3=80
180:3=26 2
26:3=8 2
8:3=2 2
24110=222213
остаток
Перевод из 10-ичной системы в 3-ичную
24110=222213
5010=
12123
50:3=16 2
16:3=5 1
5:3=1 2
5010=12123
2013
Слайд 22двенадцатеричная система счисления
12-основание
0,1,2,3,4,5,6,7,8,9,A,B-алфавит
Число двенадцать (дюжина) даже составляла конкуренцию десятке в
борьбе за статус общеупотребительной системы счисления. Дело
в том, что число
12 имеет больше делителей(2,3,4,6), чем 10(2,5). Поэтомув 12-ричной системе гораздо удобнее производить расчёты, нежели в десятичной.
Дюжина гораздо прочно вошла в нашу жизнь.
Выражается это хотя бы в следующем,
многие предметы(столовые приборы,
карандаши, фломастеры, платки)
до сих пор продаются дюжинами.
Слайд 23десятеричная система счисления
10-основание
0,1,2,3,4,5,6,7,8,9-алфавит
«Преимущество десятичной системы не математическое,
а
зоологическое. Если бы у нас на руках было не десять
пальцев, а восемь, то человечество пользовалось бы восьмеричной системой» (Н.Н. Лузин)Самая распространённая в мире система счисления.
Слайд 24Соответствие первых двух десятков двоичной
и десятичной систем счисления
Десятичная
0 1 2 3 4 5
6 7 8 9Двоичная 0 1 10 11 100 101 110 111 1000 1001
Десятичная 10 11 12 13 14 15 16 17 18 19
Двоичная 1010 1011 1100 1101 1110 1111 10000 10001 10010 10011
Необыкновенная девочка
Поможет нам двоичная система счисления.
Ей было 1100 лет,
Она в 101-й класс ходила,
По 100 книг носила,
Получается совсем обычная картина.
значит 12 лет
т.е. в 5 класс
значит по 4 книги.
Слайд 25рефлексия
Подошёл к концу наш урок. Давайте подведем итоги.
У вас у каждого на парте лежат смайлики, поднимите, пожалуйста,
тот,который расскажет о вашем настроении после урока, о впечатлении от урока.
Кто из вас выскажет мнение о пройденном уроке, вот фразы, с которых вы мо-
жете начать…
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Слайд 26Литература, ресурсы интернет
О. М Шаров. Н. А. Меньшикова. Н. М.
Ефимова.
Организация внеклассной работы по математике в средней школе.
Энциклопедия для
детей. Т.11.Математика / М.Аксёнова, В.Володин и др.-М.: Аванта, 2005.-688с.:ил.
История систем счисления http://comp-science.narod.ru/Demenev/files/
history.htm
Аудиофайлы http://www.tamada-smirnov.ru/fanfar.php
http://images.yandex.ru/yandsearch?text=%D0%B0%D0%
BD%D0%B8%D0%BC%D0%B0%D1%88%D0%BA%D0%
B8%20%D0%B1%D0%BB%D0%B5%D1%81%D1%82%
D1%8F%D1%88%D0%BA%D0%B8&stype=image
Анимация, картинки