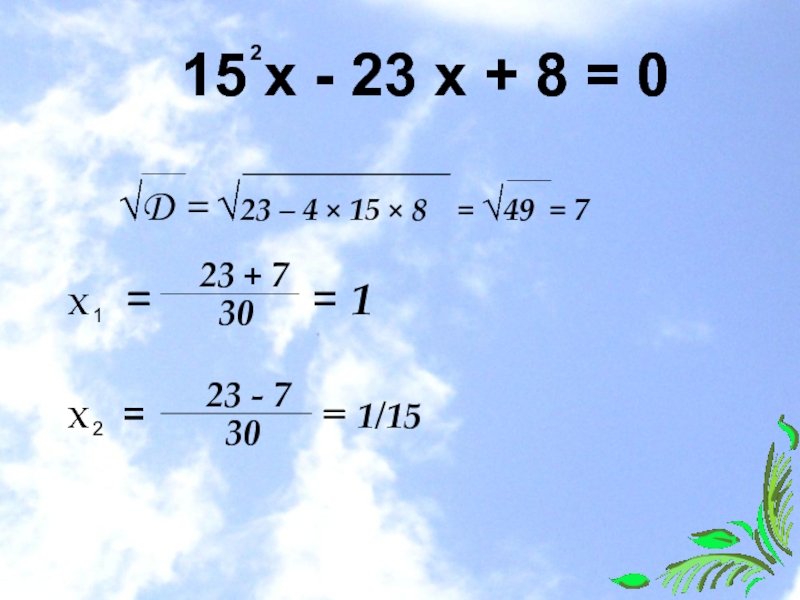Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы уравнений (11 класс)
Содержание
- 1. Системы уравнений (11 класс)
- 2. Уравнение записывают одно под другим и объединяют
- 3. Система двух уравнений, из которых одно первой
- 4. Пусть дана система: 4 у + х
- 5. Тогда уравнение 2-й степени после подстановки дает
- 6. Решаем уравнение - 4(2х-1)
- 7. 15 х -
- 8. После этого из уравнения у = 2х
- 9. Таким образом, данная система имеет две
- 10. Система двух уравнений, из которых каждое второй
- 11. Если b = 0, то и
- 12. Умножив обе части на x , получим
- 13. Подобным же образом решается и система:
- 14. Надо решить систему уравнений:
- 15. I способ (графический) Построим в одной координатной
- 16. Из рисунка видно, что значения корней следующие:
- 17. II способ (аналитический)Умножим второе уравнение на 2
- 18. Задача сводится к системе линейных уравнений с двумя неизвестными:
- 19. Применяя к полученным системам метод сложения (т.е.
- 20. Решить систему уравнений:
- 21. I способ (графический) Построим в одной координатной
- 22. Ответ: . (2;-3); (-2;-3); (3;2); (-3;2)
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Проект по математике
Системы уравнений
На тему:
Выполнила: ученица 11 класса Грибской СОШ
Тафинцева Настя
Слайд 2Уравнение записывают одно под другим и объединяют фигурной скобкой. Порядок
уравнений не играет роли.
Например:
х+у=39
х-у=11
Системой уравнений называется множество уравнений, решаемых совместно.
называется множество пар (х;у), удовлетворяющих каждому уравнению.
Обозначение.
5х+3у=7
2х+3у=1
Решением системы
уравнений с 2 переменными
Слайд 3Система двух уравнений,
из которых одно первой степени,
а другое
второй.
Система уравнений вида:
х + у = а
ху = b.
Уравнение первой степени
Уравнение второй степени
Слайд 4Пусть дана система:
4 у + х + 3у =
1
2 х – =
Воспользуемся способом подстановки
у
1
2
выразим из второго уравнения у.Слайд 5Тогда уравнение 2-й степени после подстановки дает уравнение с одним
неизвестным х:
4 у + х + 3у = 1
2 х – 1 = у-4(2х-1) +х+3(2х-1)=1
2
Слайд 6Решаем уравнение
- 4(2х-1) + х +
3(2х-1)=1
2
х – 4 (2х-1) + х + 3 (2х -
1) = 1х – 4 (4х – 4х + 1) + х +6х – 3 = 1
х – 16х + 16х - 4 + х + 6х – 3 – 1 = 0
-15х + 23х – 8 = 0; 15х – 23х + 8 = 0
2
2
2
2
2
2
2
2
Слайд 9 Таким образом, данная система имеет две пары решений:
1) x1 =
1 , y1 = 1;
2) х2 = 8/15 , y2 = 1/15
Ответ: ( 1;
1) ;(8/15 ; 1/15)Слайд 11 Если b = 0, то и х = 0
и у = 0 . Поэтому мы можем, не нарушая
равносильности уравнений, разделить обе части второго из них на х:x² + ( b/x )² = a
у = b/x
x² + y² = а
х у = b
<=>
Слайд 12Умножив обе части на x , получим равносильное уравнение:
x
+ b = ax , т. е.
x — ax +
b = 0.2
4
4
2
2
2
2
Слайд 15I способ (графический)
Построим в одной координатной плоскости графики функций
х ² + у ² = 25
х • у = 12
<=>
х ² + у ² = 25
у = 12 / х
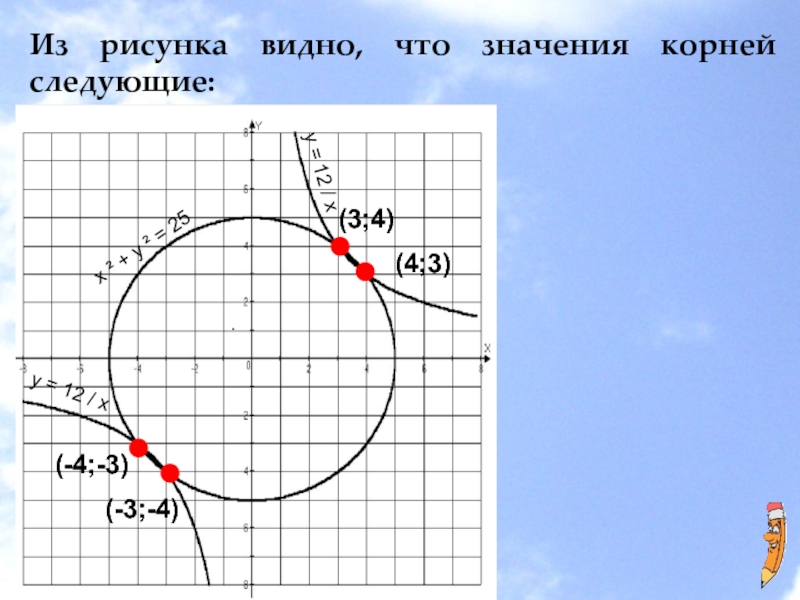
Слайд 16Из рисунка видно, что значения корней следующие:
.
х ² +
у ² = 25
у = 12 / х
у = 12
/ х(-4;-3)
(-3;-4)
(3;4)
(4;3)
Слайд 17II способ (аналитический)
Умножим второе уравнение на 2 и сначала сложим
с первым, а затем вычтем из первого. Получим:
× 2
Слайд 19Применяя к полученным системам метод сложения (т.е. сперва сложим эти
уравнения, а далее вычтем из первых – вторые), получим:
Ответ:
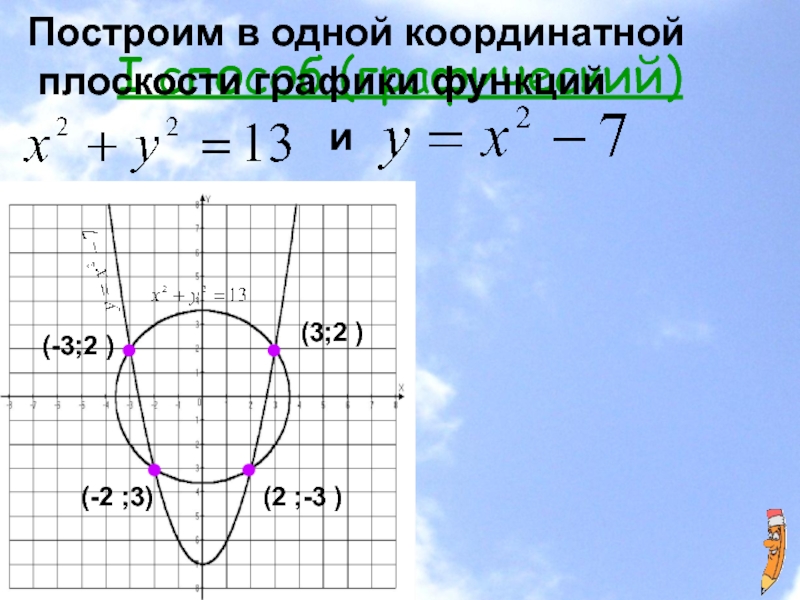
(4;3) ; (-3;-4) ; (3;4) ; (-4;-3)Слайд 21I способ (графический)
Построим в одной координатной плоскости графики функций
(-3;2 )
(-2 ;3)
(3;2 )
(2 ;-3 )