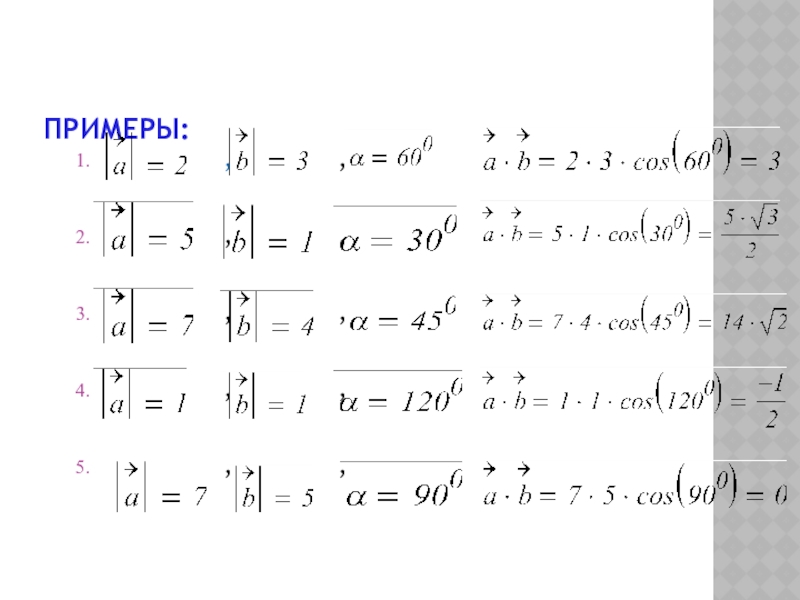Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Скалярное произведение векторов.
Содержание
- 1. Скалярное произведение векторов.
- 2. УСТНО:cos 450 = tg 450 =cos 600
- 3. ДИКТАНТ ДАНЫ ТОЧКИ A(2; -3), B(-1; 2),
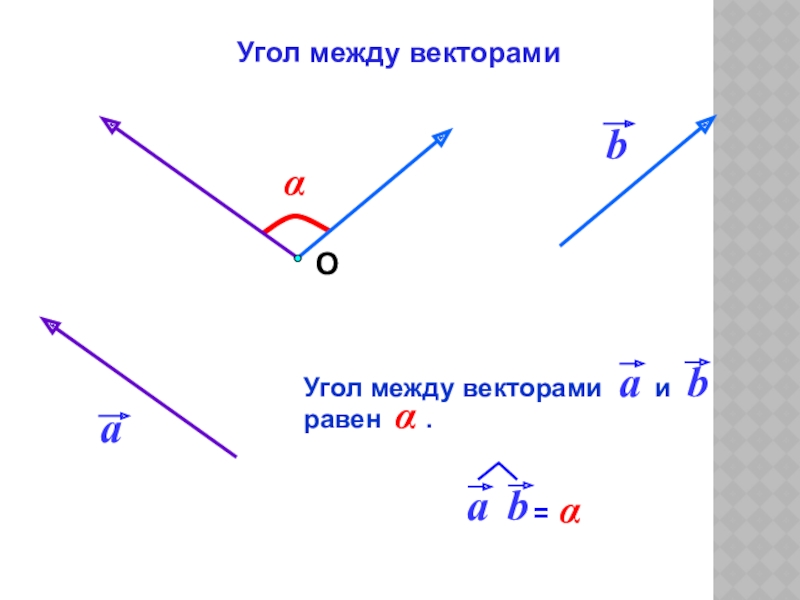
- 4. αОУгол между векторами
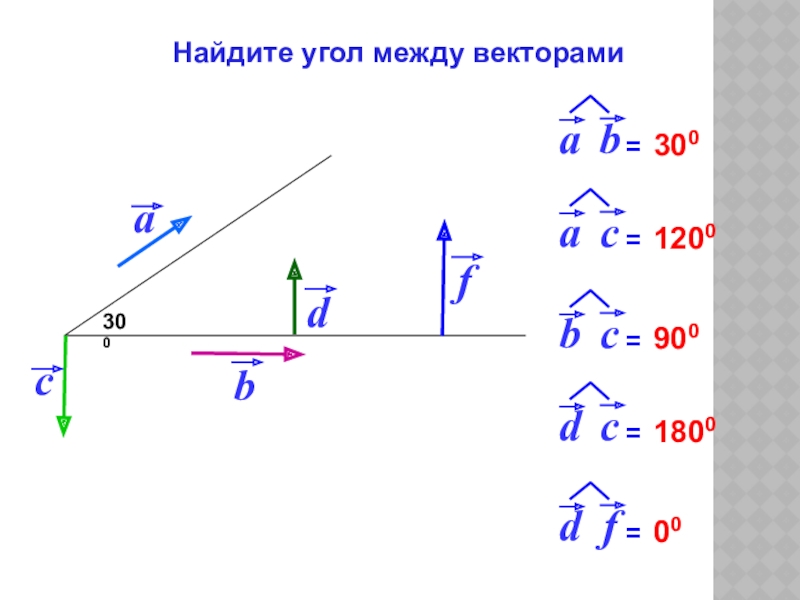
- 5. 300 3001200 900 1800 00 Найдите угол между векторами
- 6. Скалярное произведение векторов – число!Скалярным произведением двух векторов называется произведениеих длин на косинус угла между ними.Определение
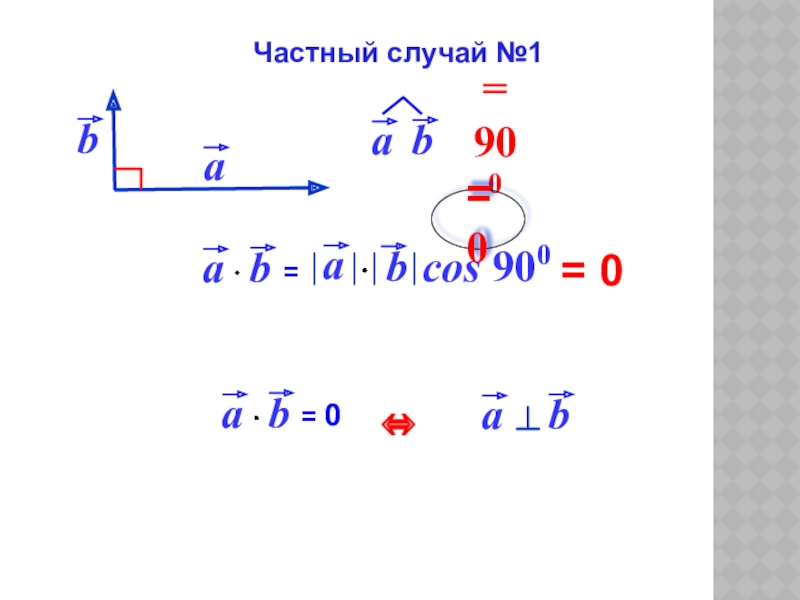
- 7. = 0 Частный случай №1= 0
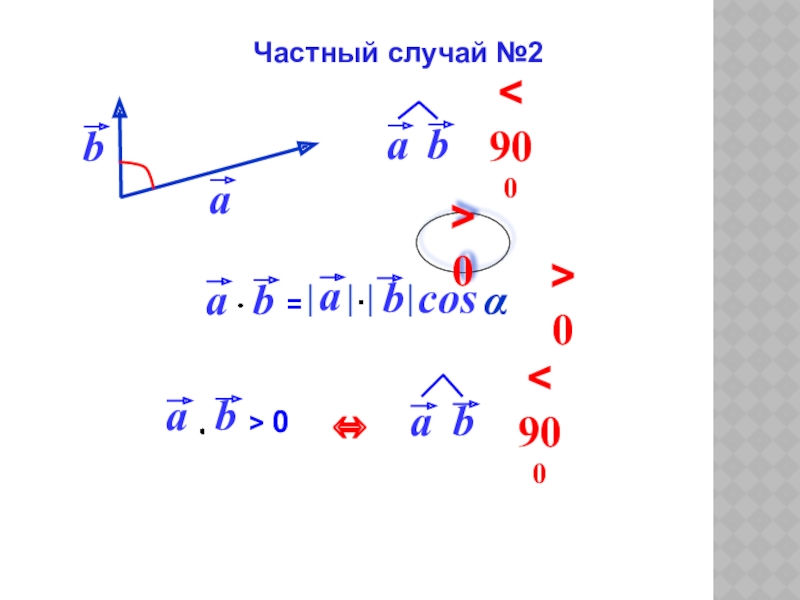
- 8. cosα > 0> 0Частный случай №2
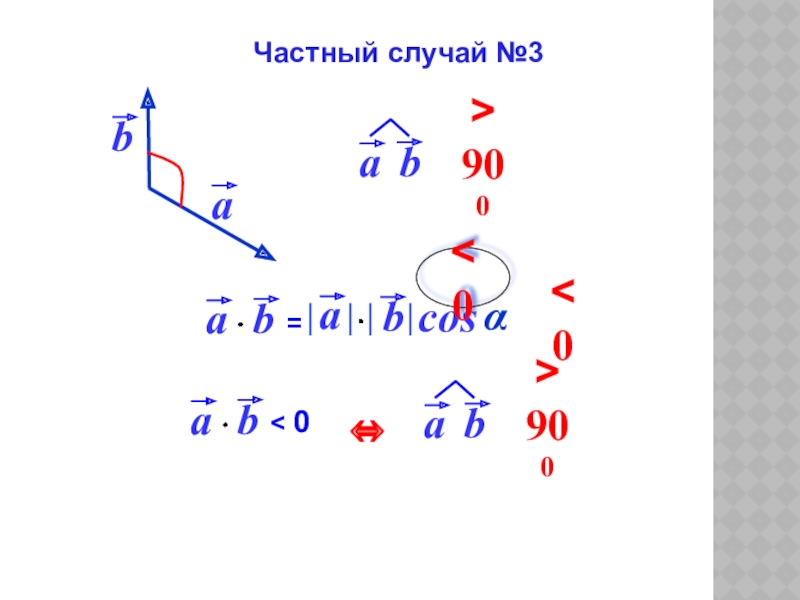
- 9. cosα < 0< 0Частный случай №3
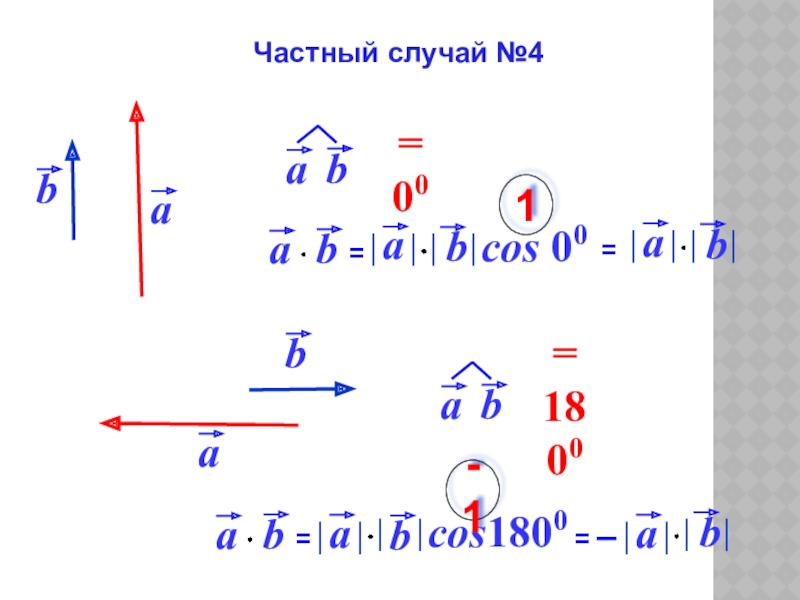
- 10. cos 001cos1800-1Частный случай №4
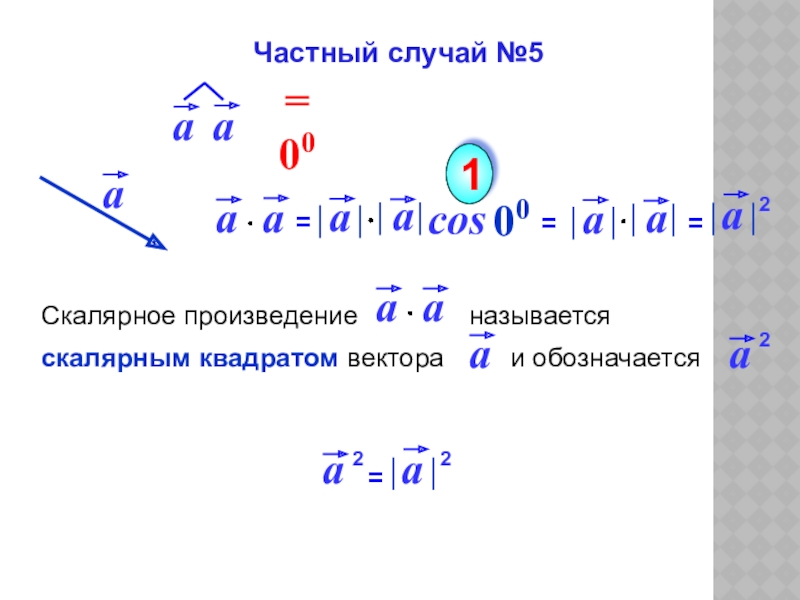
- 11. cos00 1Частный случай №52222
- 12. ПРИМЕРЫ: ,
- 13. Формула для нахождения скалярного произведениячерез координаты векторов= x1x2 + y1y2
- 14. Пример №1Найти скалярное произведение векторов:a {-6; 9}b {-1; 0}
- 15. Пример №2Найти скалярное произведение векторов:a {0; 0}b {22; 1}
- 16. ВЫЧИСЛИТЕ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ:a(1,1); b(1,2)a(-2,5); b(-9,-2)a(-3,4); b(4,5)a(5,2); b(-9,4)a(-1,1); b(1,1)
- 17. НЕНУЛЕВЫЕ ВЕКТОРЫ ПЕРПЕНДИКУЛЯРНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ИХ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ РАВНО НУЛЮ.№1047(а)Решение.СЛЕДСТВИЕ 1
- 18. Следсс2.Сседствие 2.СЛЕДСТВИЕ 2
- 19. Вычислите скалярное произведение векторов:Вычислите длину вектора a:
- 20. Скачать презентанцию
УСТНО:cos 450 = tg 450 =cos 600 =sin 300 =sin 600 =sin 900 =cos 900 =tg 450 =tg 900 =sin2 x + cos2 y =
Слайды и текст этой презентации
Слайд 3ДИКТАНТ
ДАНЫ ТОЧКИ A(2; -3), B(-1; 2), С(0; -4)
Найдите координаты вектора
AB
Найдите координаты вектора ВС
Найдите длину вектора AB
Найдите длину вектора BC
Произведение
5 · AB :Слайд 6Скалярное произведение векторов – число!
Скалярным произведением двух векторов называется произведение
их
длин на косинус угла между ними.
Определение
Слайд 16ВЫЧИСЛИТЕ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ:
a(1,1); b(1,2)
a(-2,5); b(-9,-2)
a(-3,4); b(4,5)
a(5,2); b(-9,4)
a(-1,1); b(1,1)
Слайд 17 НЕНУЛЕВЫЕ ВЕКТОРЫ ПЕРПЕНДИКУЛЯРНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА ИХ СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ РАВНО НУЛЮ.
№1047(а)
Решение.
СЛЕДСТВИЕ 1
Слайд 19Вычислите скалярное произведение векторов:
Вычислите длину вектора a:
Вычислите длину вектора
b:
Вычислите косинус угла между векторами:
Сделайте вывод: тупой, прямой или
острый угол мы получилиДАНО:
угол острый