Слайд 1Десять способов решения
квадратного уравнения
Слайд 2
Данный проект рассчитан на учащихся 8 класса. Может быть применен
в классах с любым уровнем подготовки.
Умением решать квадратные уравнения овладевают
практически все выпускники средней школы. Но чаще всего учащиеся для нахождения корней уравнения применяют только единственный способ: через применение формул для вычисления дискриминанта и корней квадратного уравнения. Но есть и другие формулы и методы решения, применение которых позволяет более рационально и быстрее решать данные уравнения, что поможет учащимся успешнее овладеть программой.
Данный проект позволит расширить область математических знаний учащихся по теме за счет изучения новых методов, не входящих в школьный курс математики.
Слайд 3Цели:
Знакомство с новыми методами решения квадратных уравнений.
Углубление знаний по теме
«Квадратные уравнения».
Развитие математических, интеллектуальных способностей, навыков исследовательской работы.
Создание условий для
самореализации личности.
Слайд 4Задачи:
Познакомить учащихся с новыми способами решения квадратных уравнений.
Закрепить умения решать
уравнения известными способами.
Ввести теоремы, позволяющие решать уравнения нестандартными способами.
Продолжить формирование
общенаучных навыков математической культуры.
Содействовать формированию интереса к исследовательской деятельности.
Создать условия для учащихся в реализации и развитии интереса к предмету математика.
Слайд 5
Данный проект предполагает компактное и четкое изложение теории вопроса и
решение типовых задач. На уроках будет использоваться фронтальный опрос, который
охватывает большую часть учащихся класса, что позволяет развивать точную лаконичную речь, способствовать работать в быстром темпе. Основные формы работы с учащимися: лекция с элементами беседы, практическая работа, самостоятельная работа, творческая поисковая работа. Проект мобильный. т.к. дает возможность уменьшить количество задач при успешном усвоении метода, а блочная подача позволит учащимся, пропустившему урок, приступить к работе, не испытывая трудностей.
Отличительной особенностью проекта является знакомство с методами решения квадратных уравнений с помощью циркуля и линейки и способом «номограмм».
Слайд 6Знать и уметь:
Теоремы о свойствах коэффициентов квадратного уравнения.
10 различных способов
решения уравнений.
Различные формулы для решения уравнений. Уверенно применять формулы, способы,
теоремы для решения квадратных уравнений.
Понимать лексику, связанную с предметом; строить, читать, понимать графики.
При вычислении применять устные и письменные приемы, пользоваться современными техническими средствами обучения.
Слайд 7
Способы
решения
квадратных
уравнений
Слайд 8Разложение на множители
левой части уравнения
Решим уравнение х2 + 10х
+24 = 0.
Разложим на множители левую часть:
х2 +
10х +24 = х2 + 12х - 2х - 24 = х(х + 12) – 2(х + 12) =
=(х + 12) (х – 2)
х + 12) (х – 2) = 0
х + 12 =0 или х – 2= 0
х = - 12 х = 2
Ответ: - 12; 2.
Решить уравнения:
х2 - х = 0; х2 + 2х = 0; х2 - 81 = 0;
х2 + 4х +3= 0; х2 + 2х -3 = 0.
Слайд 9Метод выделения
полного квадрата
Решим уравнение х2 + 6х - 7
= 0.
Выделим полный квадрат двучлена:
х2 + 6х - 7 = х2 + 2х∙ 3 + 32 – 32 - 7 = (х +3 )2 - 16
(х +3 )2 - 16 = 0
х(х +3 )2 = 16
(х +3 ) = 4 или (х +3 ) = - 4
х = 1 х = -7
Ответ: -7; 1.
Решить уравнения:
х2 - 8х + 15 = 0; х2 + 12х + 20 = 0; х2 - 6х + 8 = 0;
х2 + 4х +3= 0; х2 + 2х - 2= 0.
Слайд 10Решение квадратных уравнений по формуле
ax2+bx+c=0,
Основные формулы: (если D>0).
Если b
– нечетное, то D = b2 - 4ac
Если b =2k,
то
Решите уравнения
2 х2 - 5х +2 = 0; 6 х2 + 5х +1 = 0.
4 х2 - 5х +2 = 0.
2 х2 - 6х +4 = 0.
х2 - 18х +17= 0.
Слайд 11Приведенное уравнение
Если в уравнении вида:
ax2+bx+c=0,
где a, b,
с ∈ R
а = 1, то квадратное
уравнение вида x2+px+q=0 называется приведенным.
Слайд 12Теорема Виета
Сумма корней приведенного квадратного трехчлена x2 + px + q = 0 равна
его второму коэффициенту p с противоположным знаком, а произведение –
свободному члену q.
Т. е. x1 + x2 = – p и x1 x2 = q
Слайд 13Применение теоремы Виета
Теорема Виета замечательна тем, что, не зная корней
квадратного трехчлена, мы легко можем вычислить их сумму и произведение,
то есть простейшие симметричные выражения x1 + x2 и x1 x2.
Слайд 14Вычисление корней
Так, еще не зная, как вычислить корни уравнения:
x2 + 2x – 8 = 0,
мы, тем не менее, можем сказать, что их
сумма должна быть равна – 2, а произведение должно равняться –8.
Слайд 15Решение уравнений
с помощью теоремы Виета
Теорема Виета позволяет угадывать целые
корни квадратного трехчлена.
Так, находя корни квадратного уравнения
x2 – 7x + 10 = 0,
можно начать с того, чтобы попытаться разложить свободный член (число 10) на два множителя так, чтобы их сумма равнялась бы числу 7.
Слайд 16
Решите уравнения
x2 - 7x – 30 = 0,
x2 + 2x – 15 = 0,
x2 - 7x + 6 = 0,
5x2 - 14x – 9 = 0,
3x2 - 5x + 2 = 0,
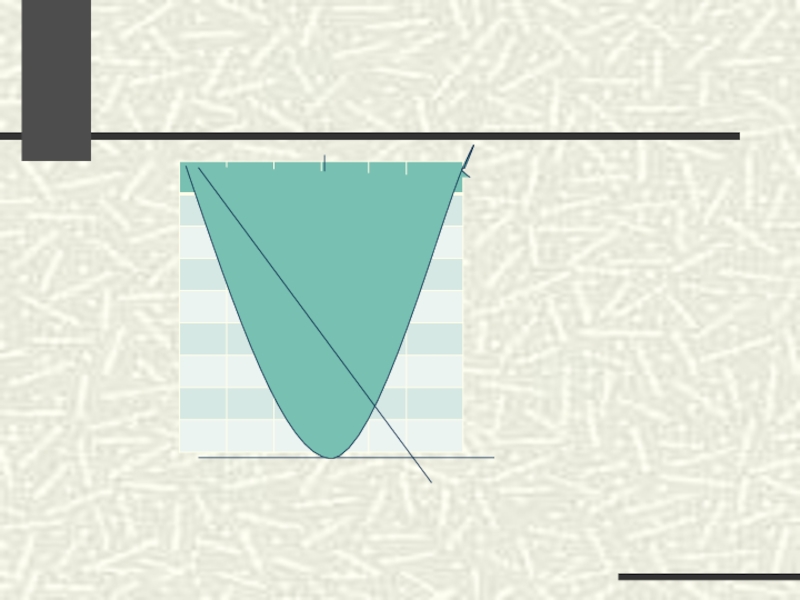
Слайд 17Графическое решение
квадратного уравнения
Решим уравнение х2 + 2х - 3
= 0.
Запишем уравнение в виде х2 = - 2х
+ 3.
В одной системе координат построим графики функций
у = х2 и у = - 2х + 3.
Обозначим абсциссы точек пересечения графиков.
Ответ: -3; 1
Слайд 18Решение уравнений с помощью циркуля и линейки
Решим уравнение ах2 +
bх + c = 0.
Построим точки:
S ( -b/2a;(a+c)/2a) – центр окружности и точка А (0;1)
Проведем окружность радиуса SA.
Абсциссы точек пересечения с осью ОХ есть корни исходного уравнения.
Слайд 19Геометрический способ решения уравнения
Решим уравнение y2 - 6у - 16
= 0.
Представим в виде y2 - 6у =
16.
На рисунке «изображено» выражение y2 - 6у , т.е. их площади квадрата со стороной у дважды вычитается площадь квадрата со стороной 3. Значит y2 - 6у + 9 есть площадь квадрата со стороной у – 3. Выполняем замену y2 - 6у = 16 у-3 3
(у – 3)2 =16 + 9 = 25
у – 3 = 5; у – 3 = - 5
у = 8; у = - 2. у
Ответ: -2; 8.
Решить уравнение:
y2 - 6у +16 = 0.
Слайд 20Решение уравнений
методом переброски
Решим уравнение ах2 + bх + c
= 0. Умножим обе части на а, получим а 2
х2 + bах + cа = 0
Пусть ах = у, откуда х = у/а. Тогда у2 + уb + cа = 0. Его корни у1 ,
у2 найдем с помощью теоремы Виета. Окончательно получаем
х1 = у/а; х2 = у/а. При этом коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, и поэтому его называют «способом переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета, и что самое важное, когда дискриминант точный квадрат.
Решим уравнение: 2х2 - 11х + 15 = 0. Перебросим коэффициент 2 к свободному члену х2 - 11х + 30= 0. Согласно теореме Виета у1 = 5; у2 = 6; х1 = 2,5; х2 = 3. Ответ: 2,5; 3.
Решить уравнение: 2х2 - 9х + 9= 0; 10х2 - 11х + 3 = 0;
3х2 + 11х + 6 = 0. 6х2 + 5х - 6 = 0. 3х2 + 1х - 4 = 0.
Слайд 21Свойства коэффициентов
квадратного уравнения
Если а+b+c=0, то х1 =1; то х2 =с/а.
Решим уравнение х2 + 6х - 7 = 0. 1
+ 6 – 7 = 0. Значит х1 =1;
х2 =-7/1 = -7. Ответ: -7; 1.
Решить уравнение:
5 х2 - 7х + 2 = 0 ;11х2 + 25х - 36 = 0; 345х2 - 137х - 208 = 0 ;
3х2 + 5х - 8 = 0; 4х2 + 5х - 9 = 0.
Если а-b+c=0, то х1 =-1; то х2 =-с/а.
Решим уравнение 2х2 + 3х + 1 = 0. 2 - 3 + 1 = 0. Значит х1 =-1; х2 =-1/2 . Ответ: -1; -1/2.
Решить уравнение:
5 х2 - 7х - 12 = 0 ;11х2 + 25х + 14 = 0; 3х2 + 5х + 2 = 0 ;
5х2 + 4х - 1 = 0; х2 + 4х + 3= 0.
Слайд 22Решение квадратных уравнений с помощью номограммы
Этот старый и незаслуженно забытый
способ решения квадратных уравнений, помещенный на стр. 83 (Брадис В.М.
Четырехзначная математическая таблица.)
Таблица XXII.Номограмма для решения уравнения
z2 +p z + g = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения. криволинейная шкала номограммы построена по формулам. Полагая ОС = p , ED = g, OE =a (все в см) из подобия треугольников CAH и CDF получаем пропорцию. Откуда после подстановок и упрощений вытекает уравнение z2 +p z + g = 0, причем буква z означаем метку любой точки кривой шкалы.
Слайд 23Информационные ресурсы
Брадис В.М. Четырехзначные математические таблицы для средней школы. –
М, Просвещение, 1992г.
Пичурин Л.Ф. За страницами учебника алгебры. – М.
Просвещение, 1990г.
Пресман А.А. Решение квадратных уравнений с помощью циркуля и линейки. – М. Квант № 4/1972г.стр.34.
Газета «Математика» № 42/2001г «Квадратные уравнения».
Литвинова С.А. «За страницами учебника математики». Издательство «Панорама» 2006г.









 0).Если b –" alt="Решение квадратных уравнений по формулеax2+bx+c=0, Основные формулы: (если D>0).Если b – нечетное, то D = b2 -">
0).Если b –" alt="Решение квадратных уравнений по формулеax2+bx+c=0, Основные формулы: (если D>0).Если b – нечетное, то D = b2 -">