Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
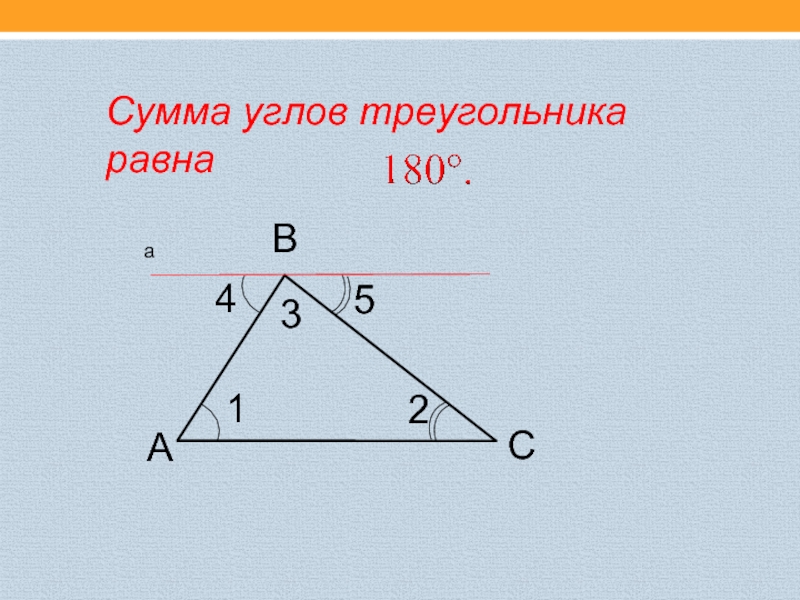
Сумма углов треугольника
Содержание
- 1. Сумма углов треугольника
- 2. «Вдохновение нужно в геометрии, как в
- 3. Математическая зарядка:Сумма углов треугольника равна 180. Углы
- 4. Встретились однажды два прямых углас углами треугольника.
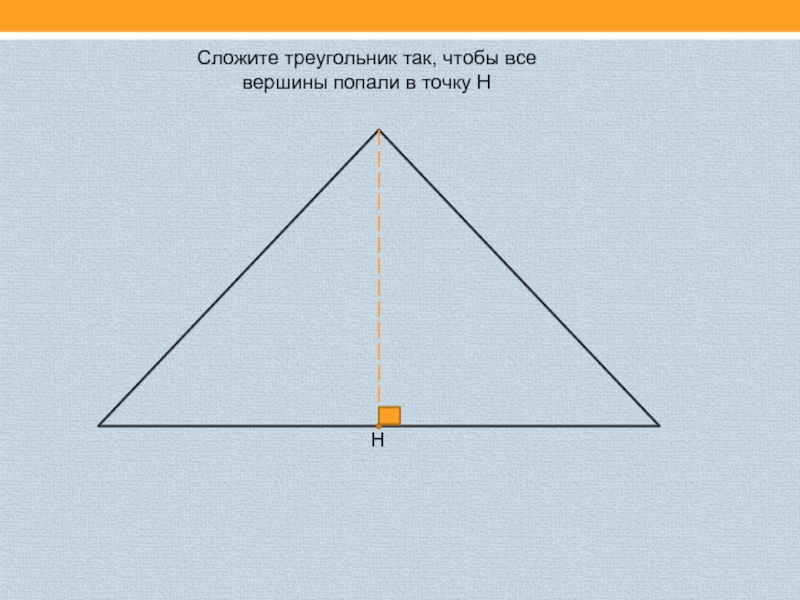
- 5. Сложите треугольник так, чтобы все вершины попали
- 6. Как, имея в наличии три равных треугольника,
- 7. Слайд 7
- 8. АВС14253а
- 9. АВС13M=
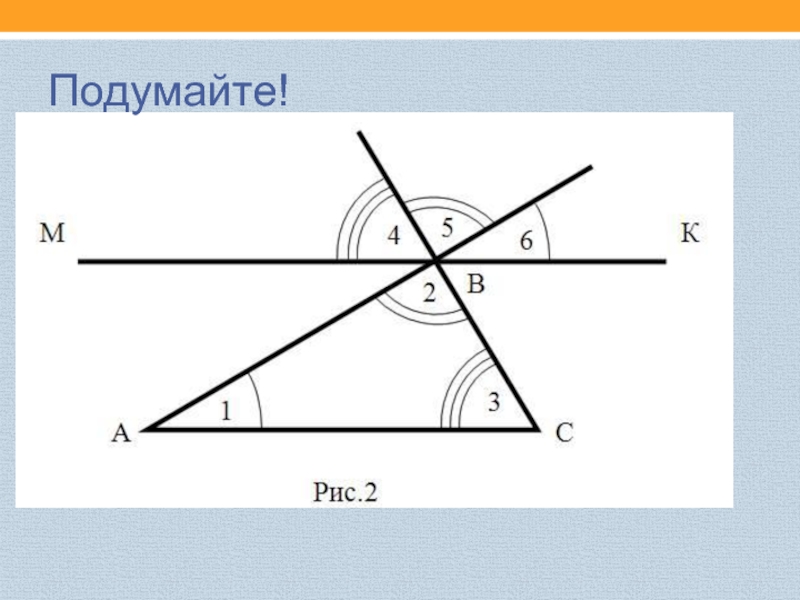
- 10. Подумайте!
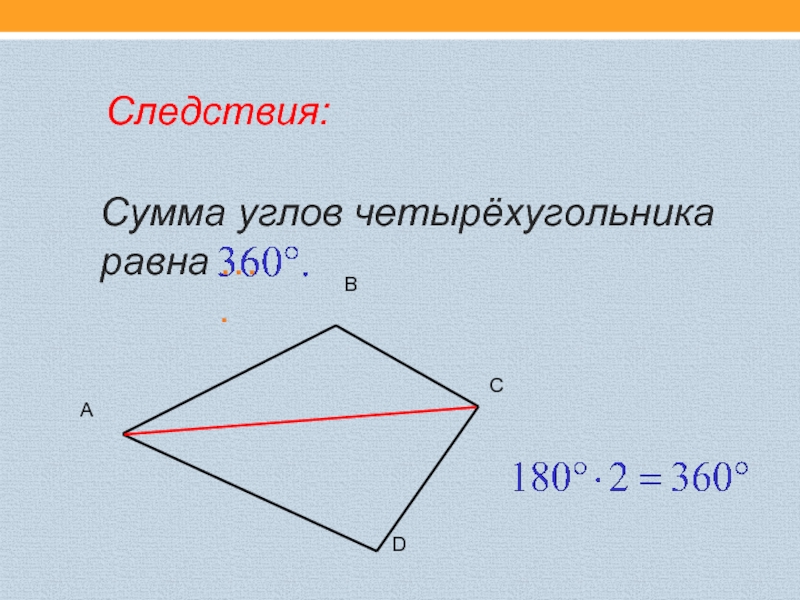
- 11. Сумма углов четырёхугольникаравна… .ABCDСледствия:
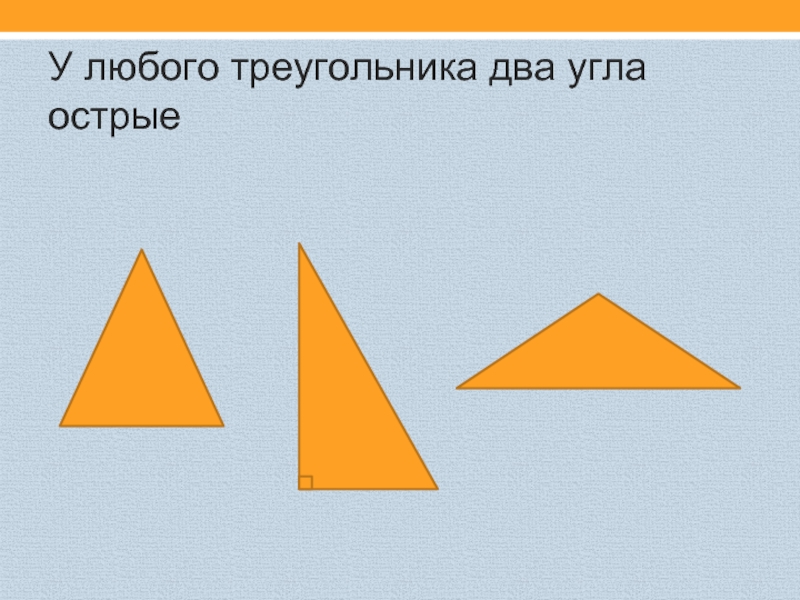
- 12. У любого треугольника два угла острые
- 13. Теорема о внешнем угле треугольника Дано: ∆
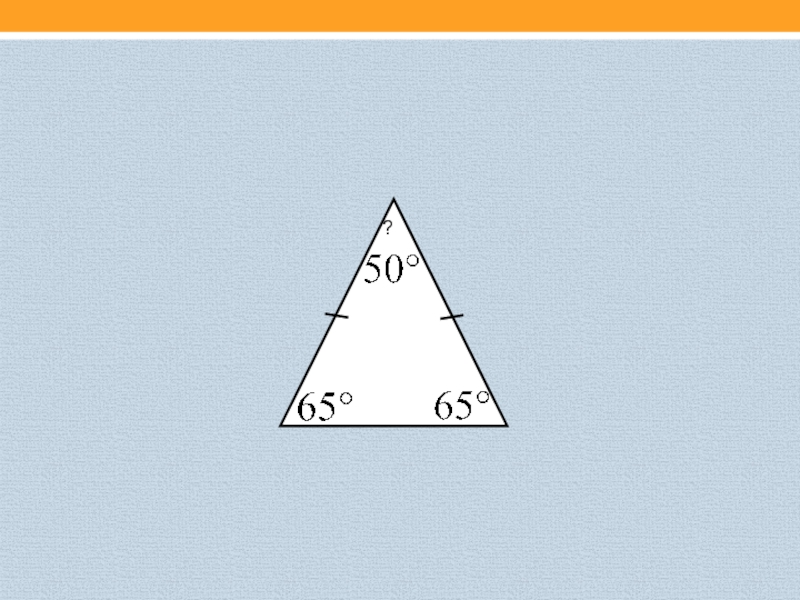
- 14. Найти неизвестный угол треугольника?
- 15. ?
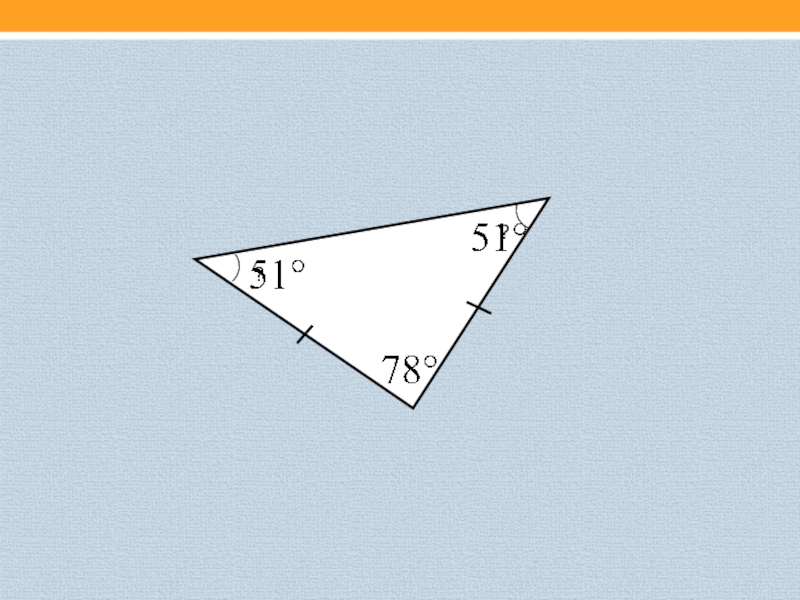
- 16. ??
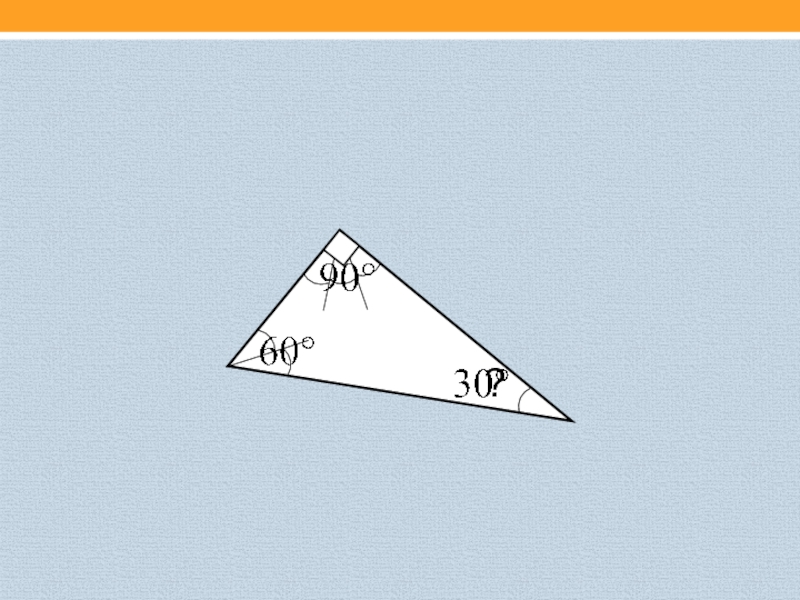
- 17. ?
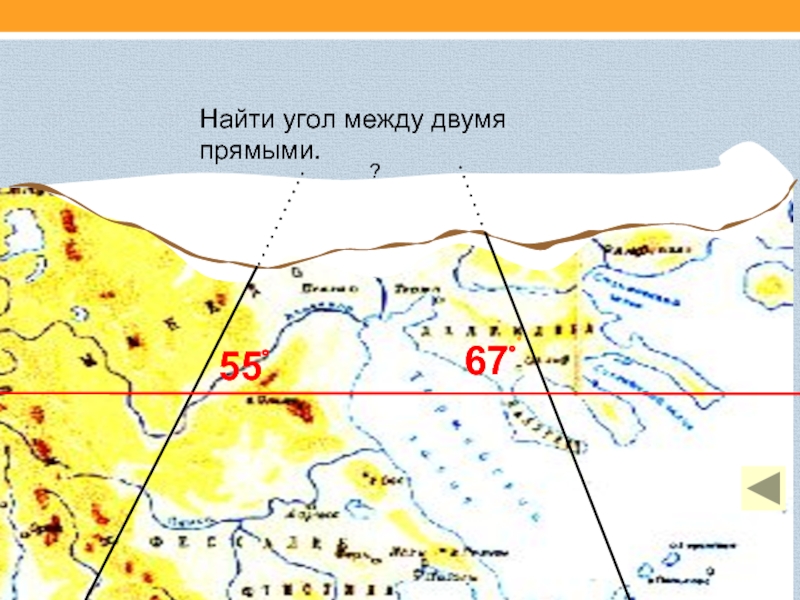
- 18. Найти угол между двумя прямыми.5567?
- 19. Примечания:На сфере сумма углов треугольника всегда превышает 180°.В плоскости Лобачевского сумма углов треугольника всегда меньше 180°.
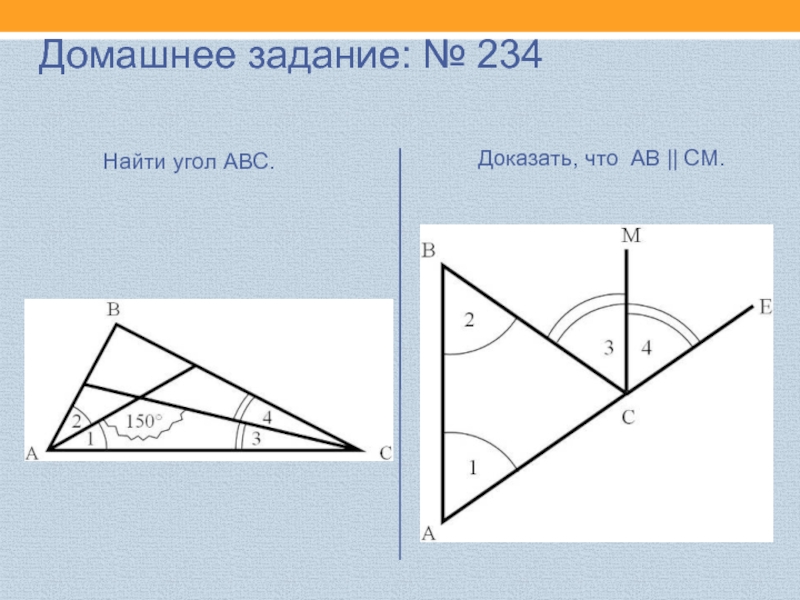
- 20. Найти угол АВС.Доказать, что АВ || СМ.Домашнее задание: № 234
- 21. Письменно: № 231
- 22. Готовимся к ГИА
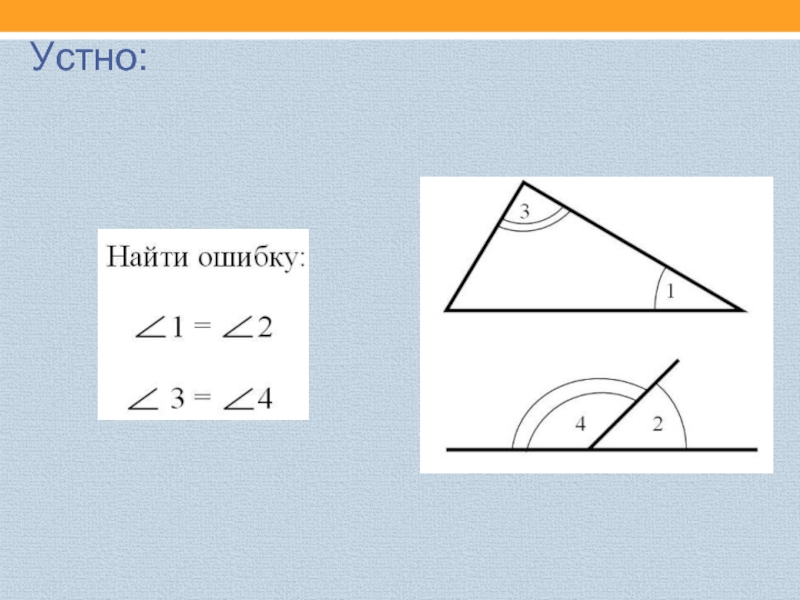
- 23. Устно:
- 24. Слайд 24
- 25. Источники информации:1.Ершова А.П., Голобородько В.В, Ершова А.С
- 26. Слайд 26
- 27. Скачать презентанцию
«Вдохновение нужно в геометрии, как в поэзии»
Слайды и текст этой презентации
Слайд 1Сумма углов треугольника
Презентацию к уроку
составила учитель математики
МБОУ СОШ № 5
г. Кстово Нижегородской области
Слайд 3Математическая зарядка:
Сумма углов треугольника равна 180.
Углы треугольника равны 180.
Сумма
углов в остроугольном треугольнике меньше 180.
Каждый угол в равностороннем треугольнике
равен 60 .Если сумма двух углов треугольника равна третьему углу, то этот треугольник прямоугольный.
Углы равнобедренного треугольника равны.
Если две прямые пересечены секущей, то накрест лежащие углы равны.
Слайд 4Встретились однажды два прямых угла
с углами треугольника. Поспорили тогда.
Одни углы
кричали: «Нас больше, нас ведь три!»
Другие отвечали: «Но в сумме
больше мы.»Услышал треугольник их этот разговор.
«Друзья мои, хотите, я разрешу ваш спор!
Зачем так много слов за спором таковым,
Сумма моих углов равна ведь двум прямым!»
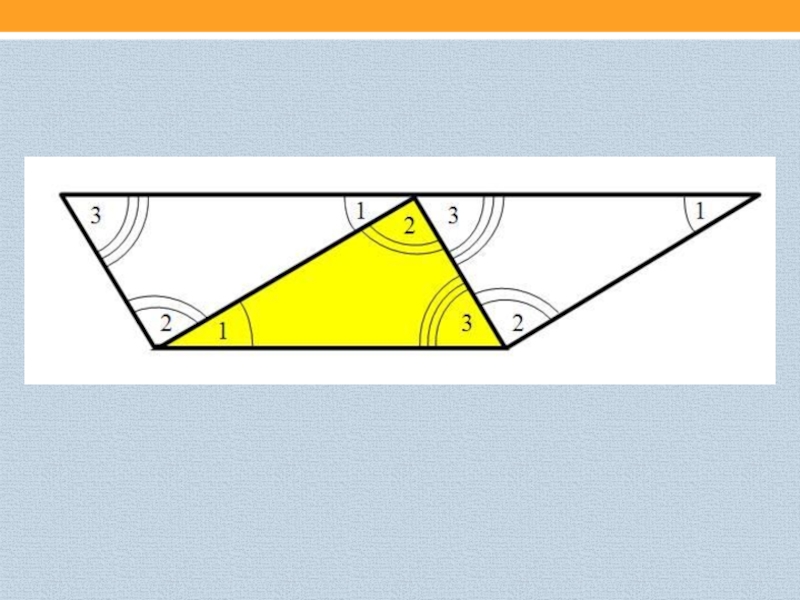
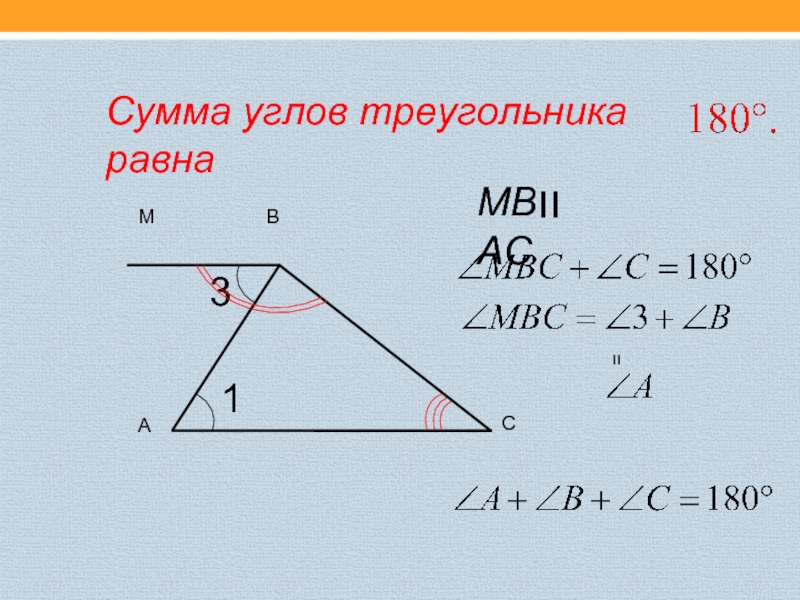
Геометрическая иллюстрация доказательства теоремы о сумме углов треугольника
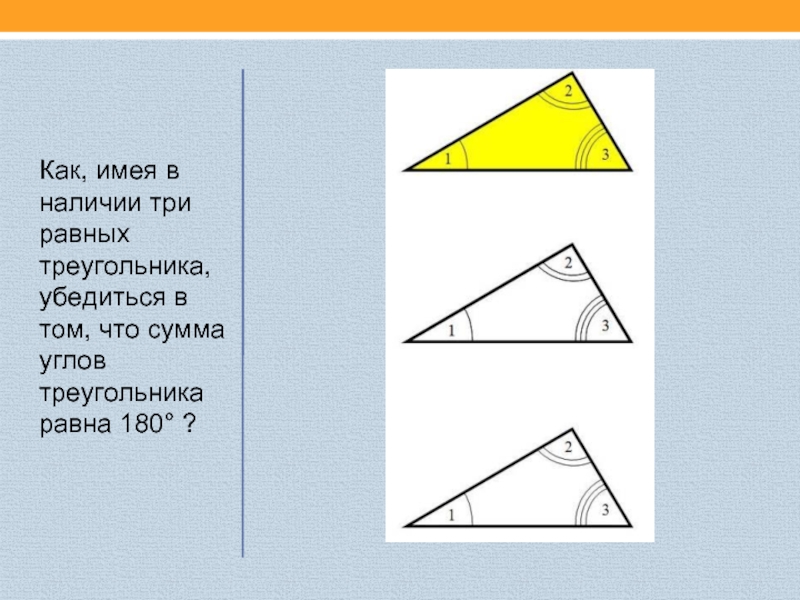
Слайд 6Как, имея в наличии три равных треугольника, убедиться в том,
что сумма углов треугольника равна 180° ?
Слайд 13Теорема о внешнем угле треугольника
Дано: ∆ АВС, 4-внешний.
1
2
3
4
Доказать:
4 = 1+ 2
Доказательство:
4+ 3=180° как смежные углы
(1+ 2) +
3=180°
4= 1+ 2
A
В
С
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним .
Слайд 19Примечания:
На сфере сумма углов треугольника всегда превышает 180°.
В плоскости Лобачевского
сумма углов треугольника всегда меньше 180°.
Слайд 25Источники информации:
1.Ершова А.П., Голобородько В.В, Ершова А.С
Самостоятельные и контрольные
работы по алгебре
и геометриидля 7 класса.-М:Илекса, 2004.-176с.
2.Саврасова С.М.,Ястребинецкий Г.А.
Упражнения
по планиметрии на готовых чертежах.-М.: просвещение, 1987.-112 с.: ил.
3. Зив Б.Г. и др.
Задачи по геометрии: Пособие для учащихся 7-11 кл.
общеобразоват.учреждений.-М.:Просвещение, 2000.-271 с.: ил.
4. http://ru.wikipedia.org/wiki/Пушкин,_Александр_Сергеевич
Теги