Разделы презентаций

Связь между функциями одного и того же аргумента

Содержание

РасшифруРРас йте

Слайды и текст этой презентации

Слайд 1Связь между функциями одного и того же аргумента

Связь между функциями одного и того же аргумента

Слайд 2РасшифруРРас йте



РасшифруРРас йте

Слайд 5Зависимость между синусом и косинусом
По определению:
y=sinα,

x=cosα
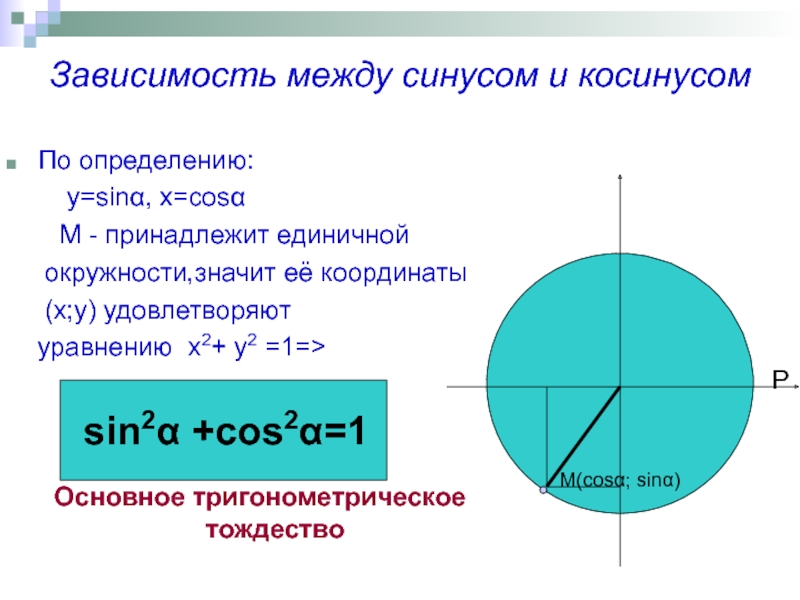
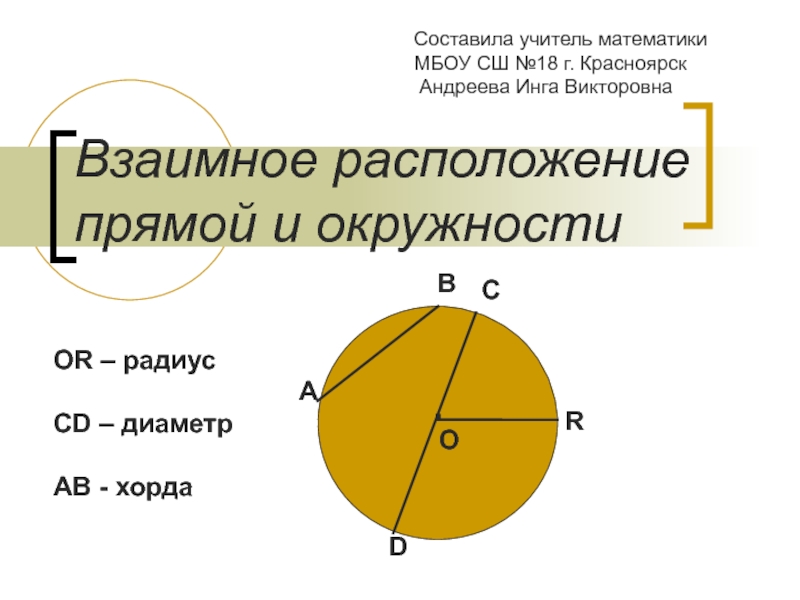
М - принадлежит единичной

окружности,значит её координаты
(х;у) удовлетворяют
уравнению х2+ у2 =1=>



Основное тригонометрическое тождество







Р



sin2α +cos2α=1









М(cosα; sinα)


Зависимость между синусом и косинусомПо определению: y=sinα, x=cosα М - принадлежит

Слайд 6Из равенства выразим sinα через cosα и cosα через sinα
sin2α

= 1- cos2α

sinα = ± √1- cos2α
cos2α = 1- sin2α



cosα = ±√1- sin 2 α

sin2α +cos2α=1

Из равенства выразим sinα через cosα и cosα через sinα sin2α = 1- cos2αsinα = ±

Слайд 8Зависимость между тангенсом и котангенсом
Перемножая равенства получим:
tg α∙ сtg α

= sinα cosα = 1

cosα sinα

tg α∙ сtg α = 1




Зависимость между тангенсом и котангенсомПеремножая равенства получим:tg α∙ сtg α = sinα cosα = 1

Слайд 9Зависимость между тангенсом и косинусом
Разделив обе части равенства
sin2α +cos2α=1

на cos2α, предполагая,
что cosα ≠ 0. Получаем:
sin2α +cos2α

1 , откуда
cos2α cos2α


1+tg2 α = 1
cos2α

Зависимость между тангенсом и косинусомРазделив обе части равенства sin2α +cos2α=1 на cos2α, предполагая, что cosα ≠ 0.

Слайд 10№2. Вычислить tgα ,если cosα = – 3/5 и

п/2 < α < п
Из формулы


Получаем: tg2α =

1 _
cos2α
=1: ( - 3/5)2 – 1 = 16/9
Тангенс во второй четверти отрицателен, зн. tgα = - 4/3

1+tg2α = 1
cos2α

№2. Вычислить tgα ,если cosα = – 3/5 и п/2 < α < пИз

Слайд 11В классе: Дома:
№

1146
№1148
№1150 (1столбик)
№1147
№1149
№1150
(2 столбик)

В классе: Дома:№ 1146№1148№1150 (1столбик)№1147№1149№1150 (2 столбик)

Похожие презентации

Прибавление чисел 7, 8, 9 1 класс Прибавление чисел 7, 8, 9 1 класс 397
Математика 1 класс Длиннее - Короче - Одинаковые по длине Математика 1 класс Длиннее - Короче - Одинаковые по длине 441
Біріктірілген 5-6 сыныптарда математика саба?ы Біріктірілген 5-6 сыныптарда математика саба?ы 316
Решение задач на умножение дробей Решение задач на умножение дробей 376
Великие математики и их открытия Великие математики и их открытия 341
Готовимся к ЕГЭ Готовимся к ЕГЭ 455
Бастауыш сыныптар бойынша жүргізілетін өзіндік жұмыстар жоспары Бастауыш сыныптар бойынша жүргізілетін өзіндік жұмыстар жоспары 460
Математика 2 класс периметр прямоугольника Математика 2 класс периметр прямоугольника 454
Многочлены от одной переменной Многочлены от одной переменной 567
Устный счёт по теме Устный счёт по теме "Решение задач на движение" 4 класс 460
Решение задач на сложение и вычитание смешанных чисел Решение задач на сложение и вычитание смешанных чисел 519
Проверяем умение решать задачи 3 класс Проверяем умение решать задачи 3 класс 346
Презентация к уроку Презентация к уроку "Кредиты" 326
Иррациональные уравнения Иррациональные уравнения 410
Подготовка к итоговой диагностической работе по математике за 2 класс Подготовка к итоговой диагностической работе по математике за 2 класс 381
Теорема Виета (8 класс) Теорема Виета (8 класс) 532
Табличное умножение Табличное умножение 442
Параллельность прямых и плоскостей Параллельность прямых и плоскостей 451
Презентация для урока математики в 5 классе на тему Презентация для урока математики в 5 классе на тему "Пирамида" 812
Презентация по математике Презентация по математике "Путешествие по Байкалу" 350

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика