Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Чевы и ее применение для решения задач (подготовка к ЕГЭ)
Содержание
- 1. Теорема Чевы и ее применение для решения задач (подготовка к ЕГЭ)
- 2. СодержаниеТеоретические факты: а)
- 3. Теоремы об отношении площадей треугольников2. Пусть ∆АВС
- 4. Теорема Менелая Если на сторонах ВС,
- 5. Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30
- 6. Джованни Чева (Ceva Giovani, 1648-1734) – итальянский
- 7. Теорема Чевы На сторонах ВС,
- 8. ЛеммаЕсли в ∆АВС некоторая прямая ВО пересекает
- 9. Доказательство теоремы Рассмотрим разбиение ∆АВС на
- 10. ЗАДАЧА. В ∆АВС на сторонах АВ, ВС
- 11. Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30
- 12. Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30
- 13. Задача. ( Математика. Подготовка к ЕГЭ. Тематические
- 14. Заключение Теоремы Чевы и Менелая не
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Методическая разработка
Рудаковой Татьяны Викторовны
Учителя математики МБОУ «Гимназия № 2»
задач (подготовка к ЕГЭ)
Слайд 2Содержание
Теоретические факты:
а) отношение площадей треугольников.
б) теорема Менелая
2. Теорема
Чевы.3. Применение теоремы для решения задач.
4. Применение теорем Чевы и Менелая при подготовке
к ЕГЭ
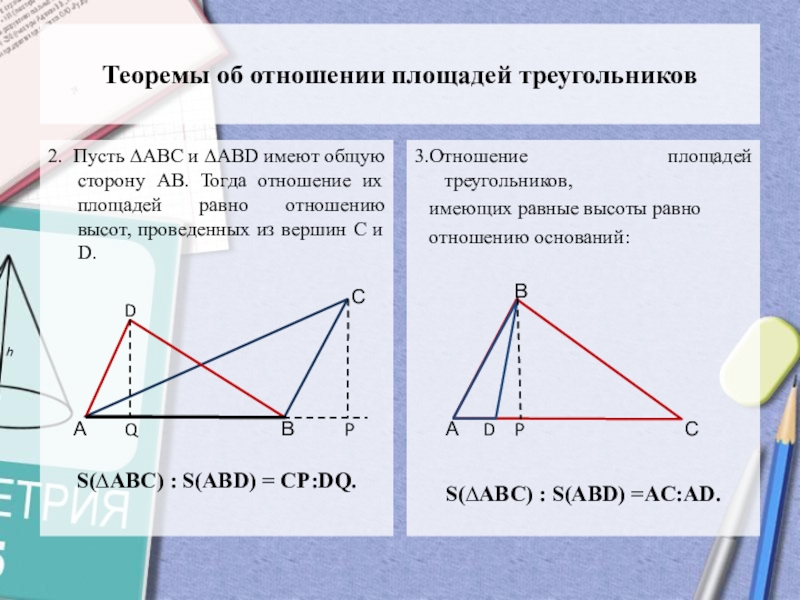
Слайд 3Теоремы об отношении площадей треугольников
2. Пусть ∆АВС и ∆АВD имеют
общую сторону АВ. Тогда отношение их площадей равно отношению высот,
проведенных из вершин С и D.S(∆АВС) : S(АВD) = СР:DQ.
3.Отношение площадей треугольников,
имеющих равные высоты равно
отношению оснований:
S(∆АВС) : S(АВD) =AC:АD.
А
В
С
D
P
Q
А
В
С
D
P
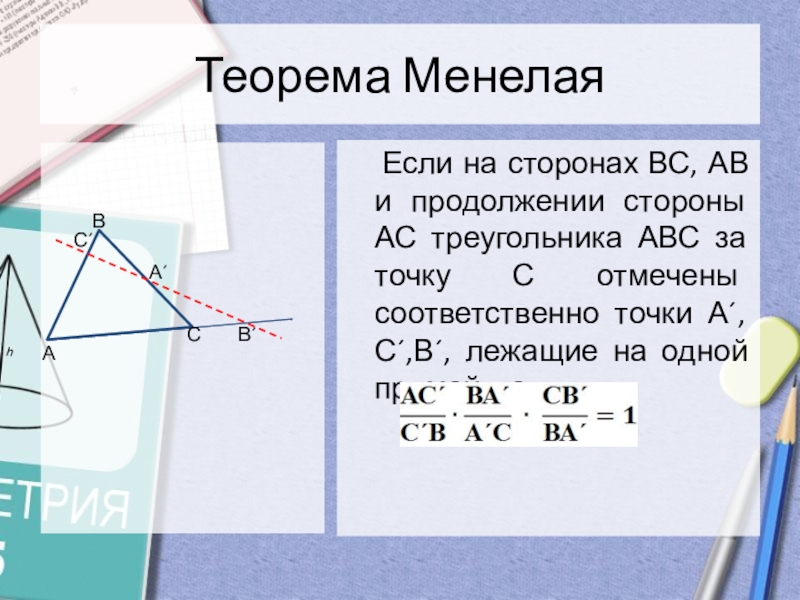
Слайд 4Теорема Менелая
Если на сторонах ВС, АВ и продолжении
стороны АС треугольника АВС за точку С отмечены соответственно точки
А´, С´,В´, лежащие на одной прямой, тоВ
А
С
В´
А´
С´
Слайд 5Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией
А.Л.Семенова, И.В.Ященко. Трениров.работа 10. С4) Точки В´ и С´ лежат
на сторонах соответственно АС и АВ ∆АВС, причем АВ´:В´С=АС´:С´В. Прямые ВВ´ и СС´ пересекаются в точке О. а) Доказать, что прямая АО делит пополам сторону ВС. б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´=1:2. Докажем, что ВК=КС.
Используем теорему Чевы.
А
В
С
В´
С´
О
К
Слайд 6Джованни Чева (Ceva Giovani, 1648-1734) – итальянский инженер и математик.
Окончил университет в Пизе. Основные его труды – работы по
геометрии и механике. Теорема, известная сегодня как теорема Чевы, была доказана им в 1678 году.Теорема Чевы: Если на сторонах AB, BC и CA треугольника ABC взяты соответственно точки C1, A1 и B1 (рис.1), то отрезки AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда выполнено равенство
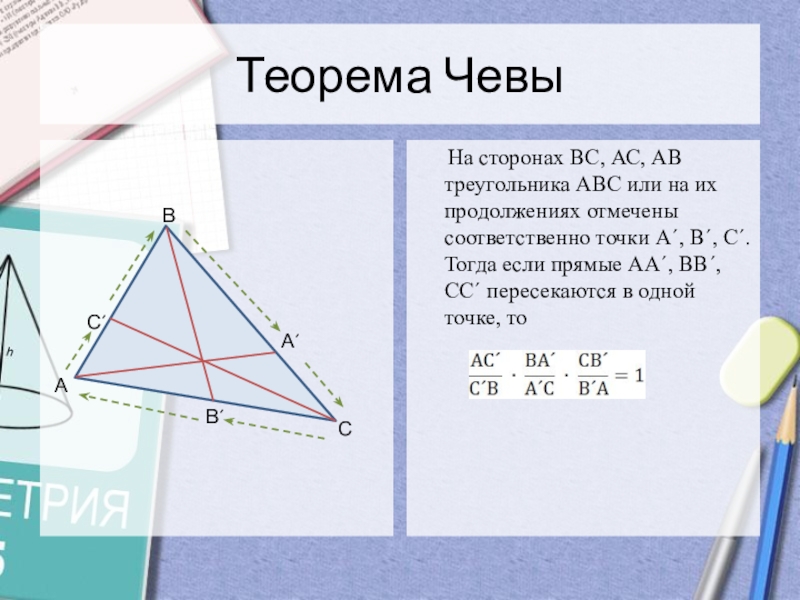
Слайд 7Теорема Чевы
На сторонах ВС, АС, АВ треугольника
АВС или на их продолжениях отмечены соответственно точки А´, В´,
С´. Тогда если прямые АА´, ВВ´, СС´ пересекаются в одной точке, тоА
В
С
А´
В´
С´
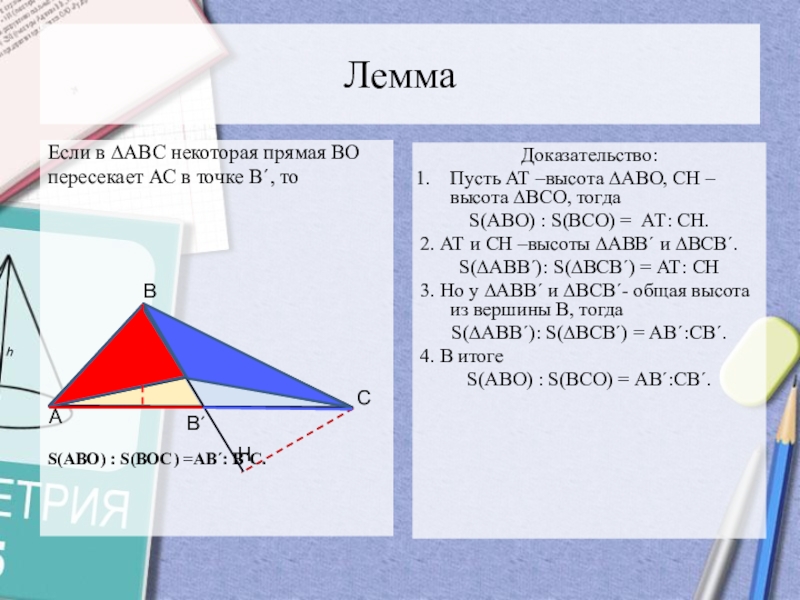
Слайд 8Лемма
Если в ∆АВС некоторая прямая ВО
пересекает АС в точке
В´, то
S(АВО) : S(ВОС) =АВ´: В´С.
Доказательство:
Пусть АТ –высота ∆АВО, СН – высота ∆ВСО, тогда
S(АВО) : S(ВСО) = АТ: СН.
2. АТ и СН –высоты ∆АВВ´ и ∆ВСВ´.
S(∆АВВ´): S(∆ВСВ´) = АТ: СН
3. Но у ∆АВВ´ и ∆ВСВ´- общая высота из вершины В, тогда
S(∆АВВ´): S(∆ВСВ´) = АВ´:СВ´.
4. В итоге
S(АВО) : S(ВСО) = АВ´:СВ´.
А
В
С
О
В´
Т
Н
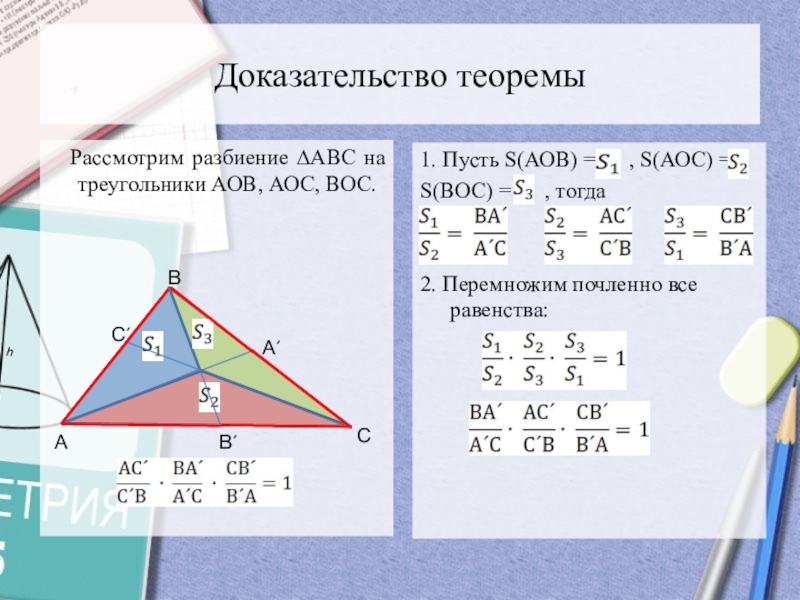
Слайд 9Доказательство теоремы
Рассмотрим разбиение ∆АВС на треугольники АОВ, АОС,
ВОС.
1. Пусть S(АОВ) = , S(АОС) =
S(ВОС)
= , тогда 2. Перемножим почленно все равенства:
А
В
С
О
А´
С´
В´
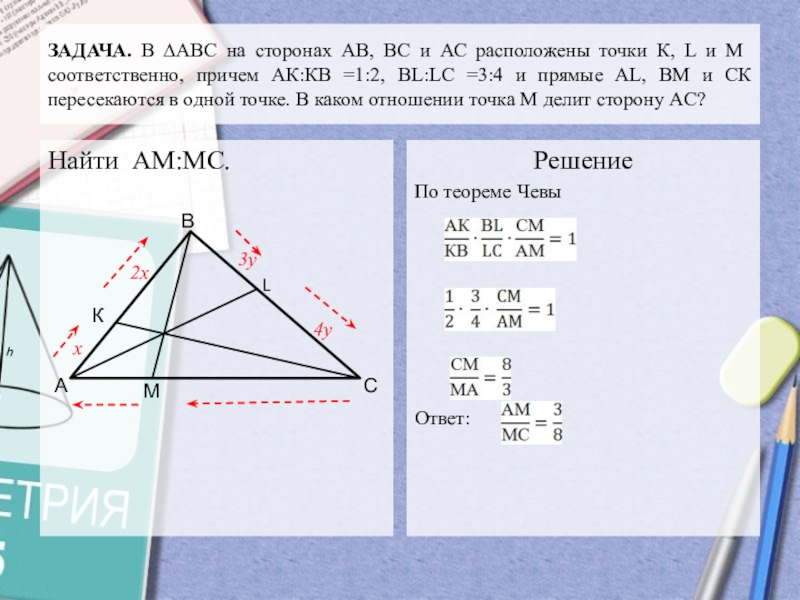
Слайд 10ЗАДАЧА. В ∆АВС на сторонах АВ, ВС и АС расположены
точки К, L и М соответственно, причем АК:КВ =1:2, ВL:LС
=3:4 и прямые АL, ВМ и СК пересекаются в одной точке. В каком отношении точка М делит сторону АС?Найти АМ:МС.
Решение
По теореме Чевы
Ответ:
В
А
С
К
L
М
х
2х
3y
4y
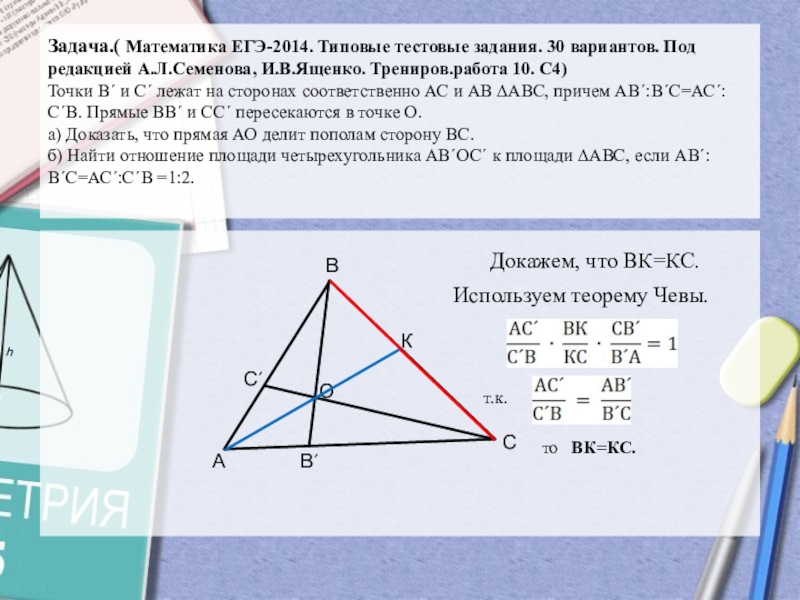
Слайд 11Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией
А.Л.Семенова, И.В.Ященко. Трениров.работа 10. С4) Точки В´ и С´ лежат
на сторонах соответственно АС и АВ ∆АВС, причем АВ´:В´С=АС´:С´В. Прямые ВВ´ и СС´ пересекаются в точке О. а) Доказать, что прямая АО делит пополам сторону ВС. б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´В =1:2. Докажем, что ВК=КС.
Используем теорему Чевы.
т.к.
то ВК=КС.
А
В
С
В´
С´
О
К
Слайд 12Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией
А.Л.Семенова, И.В.Ященко. Трениров.работа 10. С4) б) Найти отношение площади
четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´В=1:2.
Найдем
Ответ:
1. Т.к. АВ´:АС= 1:3, то
2. По теореме Менелая найдем
Для ∆АВВ´ и секущей СС´:
;
Значит =3.
3. , значит
= =
С´
х
2х
С
у
2у
3z
z
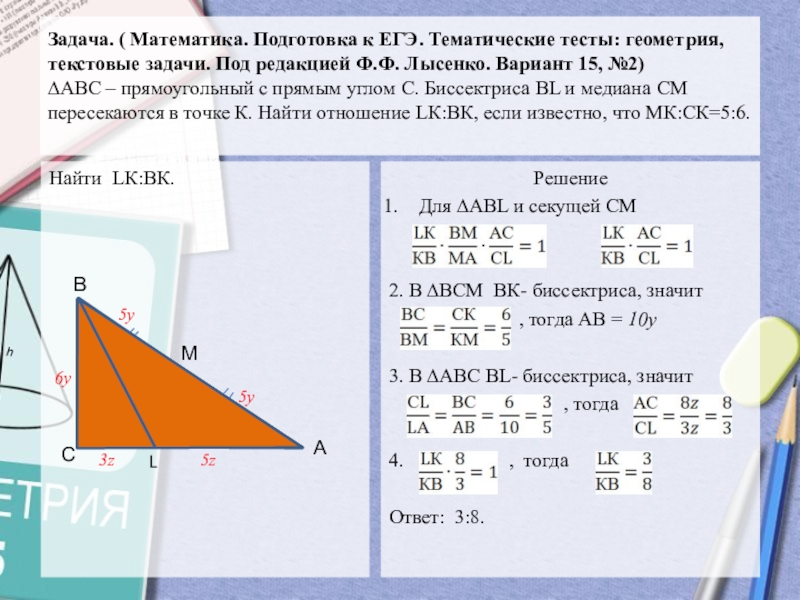
Слайд 13Задача. ( Математика. Подготовка к ЕГЭ. Тематические тесты: геометрия, текстовые
задачи. Под редакцией Ф.Ф. Лысенко. Вариант 15, №2) ∆АВС –
прямоугольный с прямым углом С. Биссектриса ВL и медиана СМ пересекаются в точке К. Найти отношение LК:ВК, если известно, что МК:СК=5:6.Найти LК:ВК.
Решение
Для ∆АВL и секущей СМ
2. В ∆ВСМ ВК- биссектриса, значит
, тогда АВ = 10у
3. В ∆АВС ВL- биссектриса, значит
, тогда
4. , тогда
Ответ: 3:8.
А
В
С
L
М
К
5х
6х
5х
К
5у
6у
5у
3z
5z
Слайд 14Заключение
Теоремы Чевы и Менелая не изучаются в основном
курсе геометрии 7–9 классов, а лишь в 11 классе. Но
трудности, связанные с освоением этих теорем, оправданы их применением при решении задач.Решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными.
Используемая литература
Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
Пособие по геометрии. Часть І. Планиметрия, векторы. В помощь учащимся 10-11-х кл.О.В.Нагорнов, А.В.Баскаков и др.М.:НИЯУ МИФИ,2009.
Математика. Подготовка к ЕГЭ. Тематические тесты: геометрия, текстовые задачи. Под ред.Ф.Ф.Лысенко. 2013г.
http://hijos.ru/2011/03/16/teorema-chevy/
http://www.resolventa.ru/demo/inform/demoinform.htm