Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Чевы и теорема Менелая и их применение
Содержание
- 1. Теорема Чевы и теорема Менелая и их применение
- 2. СодержаниеВведениеКраткая биография Чевы и МенелаяТеоремыРешение задачЗаключениеСписок литературы
- 3. ВведениеВ курсе геометрии рассматриваются важные и интересные
- 4. (Ceva Giovanni),
- 5. Менелай АлександрийскийМенела́й Александри́йский (Μενέλαος ὁ Αλεξανδρεύς, ок.
- 6. Менелаем были написаны не дошедшие до нас
- 7. Теорема Менелая. Пусть точка
- 8. Теорема Чевы.
- 9. 1. Пусть AD
- 10. 2. На стороне
- 11. 3. Стороны треугольника 5, 6 и 7.
- 12. 4. Биссектрисы BE и AD треугольника ABC
- 13. Треугольники QBD и ЕВС имеют общий угол,значит,
- 14. 5. В треугольнике ABC, площадь которого равна
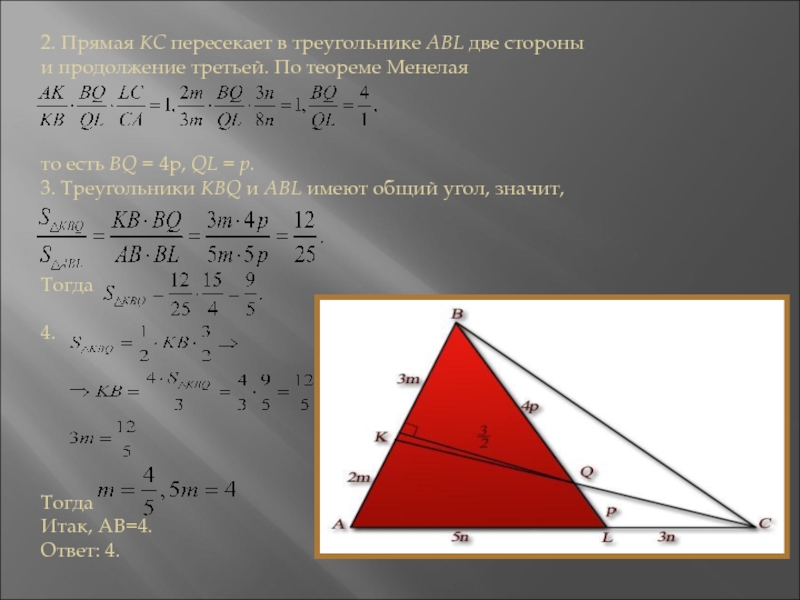
- 15. 2. Прямая КС пересекает в треугольнике ABL
- 16. Решение задач по теореме Чевы ДжованниИспользуя теорему
- 17. Используя свойства касательных, проведенных к окружности из
- 18. 2.Докажите теорему: медианы треугольника пересекаются в одной
- 19. 2. Пусть О — точка пересечения медиан.
- 20. 3.Докажите теорему: биссектрисы треугольника пересекаются в одной
- 21. В заключении1.Для решения задач необходимо находить треугольник,
- 22. Литература1.Геометрия 7-9 Л.С. Атанасян, В.Ф. Бутузов, Москва,
- 23. Скачать презентанцию
СодержаниеВведениеКраткая биография Чевы и МенелаяТеоремыРешение задачЗаключениеСписок литературы
Слайды и текст этой презентации
Слайд 2Содержание
Введение
Краткая биография Чевы и Менелая
Теоремы
Решение задач
Заключение
Список литературы
Слайд 3Введение
В курсе геометрии рассматриваются важные и интересные свойства геометрических фигур
на плоскости, но многие удивительные соотношения и изящные геометрические факты
не входят в основной курс.Работа посвящена теоремам Чевы и Менелая. Эти теоремы позволяют легко и изящно получить решение, в то время как традиционные подходы приводят к громоздким преобразованиям.
Слайд 4 (Ceva Giovanni), родился 3.3.1648, Милан
- умер 13.12.1734, Мантуя.
Итальянский
математик. Главными предметами его занятий были геометрия и механика. Он написал сочинения: "De lineis rectis se invicem secantibus statica constructio" (Милан, 1678); "Opuscula mathematica de potentiis obliquis, de pendulis et vasis et de fluminibus" (там же, 1682); и несколько других. Самым замечательным из них было первое. В первой его части автор доказывает теорему Менелая и ряд сходных с нею теорем при помощи статического метода, основанного на свойствах центра тяжести системы точек. Прилагаемый к вопросам, в которых рассматриваются отношения между отрезками, образованными пересекающимися линиями друг на друге, он состоит в помещении в точках пересечения тяжестей, обратно пропорциональных соответствующим отрезкам, и в последующем за тем выводе отношения между тяжестями на основании принципа рычага в статике. Достаточно назвать известное в геометрии под именем теоремы Ц. предложение о произведениях отрезков, образованных на сторонах треугольника трансверсалями, проходящими через общую точку (произведение трех отрезков, не сходящихся попарно в одной общей точке, равно произведению трех других отрезков), и на подобное же предложение об отрезках, образованных на сторонах четырехугольника плоскостью, их пересекающею, если не все вершины четырехугольника лежат в одной плоскости. Во второй части идеи и теоремы, изложенные в 1-й, прилагаются к коническим сечениям. Наконец, прибавление занимается теоремами о площадях некоторых плоских фигур и об объемах и центрах тяжести тел вращения второго порядка. Его брат, Томмазо Ч., математик (1648 — 1737), иезуит. В 1695 г. изобрел инструмент для механического деления угла на три части. Написал: "De natura gravium" (1669); "De ratione aequilibri. De sectione geometrico-harmonica et arithmetica etc." (1699); "Opuscula mathematica" (1699).Чева Джованни
Слайд 5Менелай Александрийский
Менела́й Александри́йский (Μενέλαος ὁ Αλεξανδρεύς, ок. 70 – от 140
н. э.) — древнегреческий математик и астроном. Время его жизни и деятельности
определяется приведёнными в «Алмагесте» Птолемея двумя астрономическими наблюдениями, которые Менелай произвёл в Риме в первом году царствования Траяна, то есть в 98 г после Р. Х..Главное сочинение Меналая — «Сферика» в трёх книгах. Его греческий оригинал утрачен, и содержание его известно по арабским, а также последующим вторичным латинским и еврейским переводам. В I книге дается определение сферического треугольника и связанных с ним понятий. В 39 предложениях этой книги речь идёт о свойствах сферических треугольников. В 21 предложении II книги рассматриваются свойства системы параллельных кругов на поверхности сферы при пересечении их разными большими кругами. Эта книга опирается на «Сферику» Феодосия. Книге III предшествуют леммы о составных отношениях, на которых строятся дальнейшие доказательства. Эта книга открывается теоремой о полном четырёхстороннике (известной также как «теорема шести величин» или «теорема о трансверсалях»). Она доказывается сначала для плоского случая, а затем переносится центральным проектированием на сферу. При этом Менелай формулирует её сферический вариант не на языке отношений синусов, как это стали делать впоследствии Ибн Ирак и другие математики стран ислама, но на языке отношений хорд.
Слайд 6Менелаем были написаны не дошедшие до нас сочинения «О вычислении
хорд» в 6 книгах, «Начала геометрии» в 3 книгах, «Книга
о треугольнике», «Книга о заходах знаков зодиака».Менелай изучал кривые высших порядков. Особенным его вниманием, по словам Паппа, пользовалась одна кривая, которая была названа им «необыкновенной линией» (παραδοξος γραμμή). Какая это была кривая, из слов Паппа, однако же, определить нельзя. По мнению П. Таннери, она представляла собой кривую, образующуюся при пересечении сферы и кругового цилиндра, радиус которого вдвое меньше радиуса сферы, а образующая проходит через центр. Эта кривая возникает в решении задачи об удвоении куба, принадлежащем Архиту Тарентскому, а из трактата братьев Бану Муса известно, что Менелай занимался этим решением.
Менелаю принадлежала «Книга о подразделении составных тел», посвящённая определению удельных весов тел. Эту книгу цитирует ал-Хазини в своей «Книге весов мудрости».
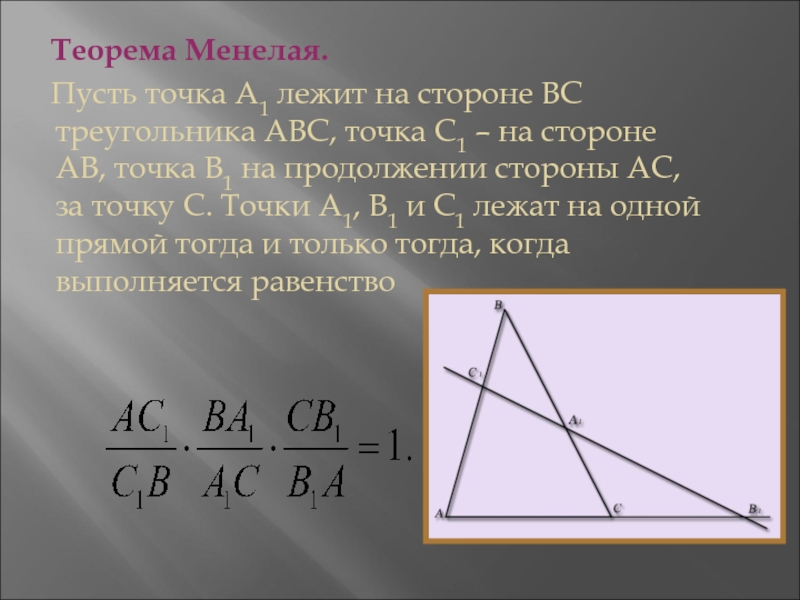
Слайд 7 Теорема Менелая.
Пусть точка А1 лежит на
стороне ВС треугольника АВС, точка С1 – на стороне АВ,
точка В1 на продолжении стороны АС, за точку С. Точки А1, В1 и С1 лежат на одной прямой тогда и только тогда, когда выполняется равенствоСлайд 8 Теорема Чевы.
Пусть в треугольнике
АВС точка А1 лежит на стороне ВС, точка В1 на
стороне АС, точка С1 – на стороне АВ. Отрезки АА1, ВВ1, СС1 пересекаются в одной точке тогда и только тогда, когда выполняется равенствоОтрезки прямых АА1, ВВ1, СС1 – «чевианы» названы по имени автора теоремы. Медианы, биссектрисы, высоты – примеры чевиан.
Слайд 9
1. Пусть AD — медиана треугольника
ABC. На стороне AD взята точка К так, что АК
: KD = = 3:1. Прямая ВК разбивает треугольник ABC на два. Найдите отношение площадей этих треугольников.Решение. Пусть AD = DC = a, KD = т; тогда АК = Зт. Пусть Р — точка пересечения прямой ВК со стороной АС. Необходимо
найти отношение . Так как треугольники АВР
и РВС имеют равные высоты, проведенные из вершины В, то =
По теореме Менелая для треугольника ADC и секущей РВ имеем:
Итак, SABP : SBPC = 3 : 2.
Ответ: 3 : 2
Решение Задач
по теореме Менелая
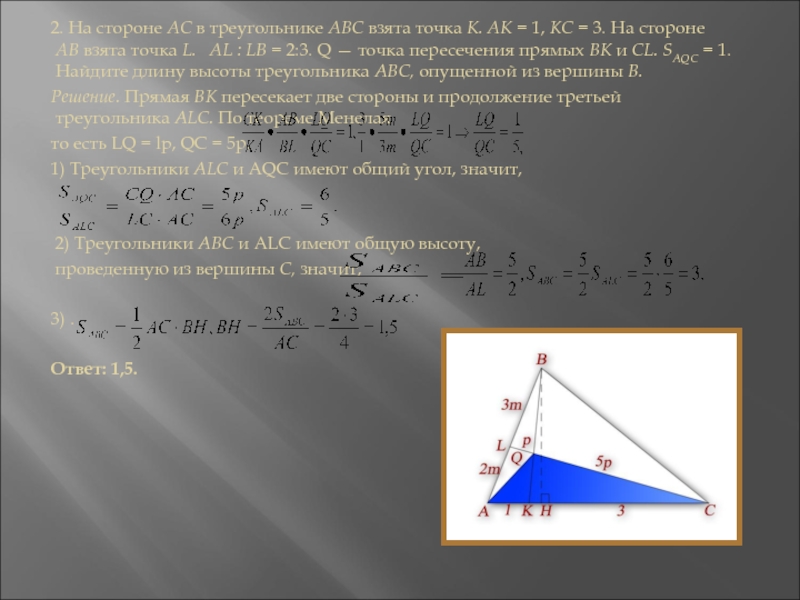
Слайд 10 2. На стороне АС в треугольнике
ABC взята точка К. АК = 1, КС = 3.
На стороне АВ взята точка L. AL : LB = 2:3. Q — точка пересечения прямых ВК и CL. SAQC = 1. Найдите длину высоты треугольника ABC, опущенной из вершины В.Решение. Прямая ВК пересекает две стороны и продолжение третьей треугольника ALC. По теореме Менелая
то есть LQ = lp, QC = 5р.
1) Треугольники ALC и AQC имеют общий угол, значит,
2) Треугольники ABC и ALC имеют общую высоту,
проведенную из вершины С, значит,
3) .
Ответ: 1,5.
Слайд 113. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков,
на которые биссектриса большего угла этого треугольника разделана центром окружности,
вписанной в треугольник.Решение. Пусть в треугольнике ABC АВ = 5, ВС = 7, АС = 6. Угол ВАС
лежит против большей стороны в треугольнике ABC, значит, угол ВАС — больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть О — точка пересечения биссектрис. Необходимо найти АО: OD. Так как AD —биссектриса треугольника ABC, то , то есть
BD = 5k, DC = 6k. Так как BF — биссектриса треугольника ABC, то
, то есть AF = 5т, FC = 7т.
Прямая BF пересекает две стороны и продолжение третьей треугольника ADC. По теореме Менелая
Ответ: 11 : 7.
Слайд 12
4. Биссектрисы BE и AD треугольника ABC пересекаются в точке
Q. Найдите площадь треугольника ABC, если ,
2АС = ЗАВ, 3BC = 4AB.Решение. Пусть АВ = а,
тогда АС = а, ВС = а.
AD — биссектриса треугольника ABC, тогда
то есть BD = 2р, DC = Зр.
BE — биссектриса треугольника ABC, тогда
AE=3k, ЕС = 4к.
В треугольнике ВEС прямая AD пересекает 2 стороны и продолжение третьей стороны. По теореме Менелая
то есть EQ = 9m, QB = 14m.
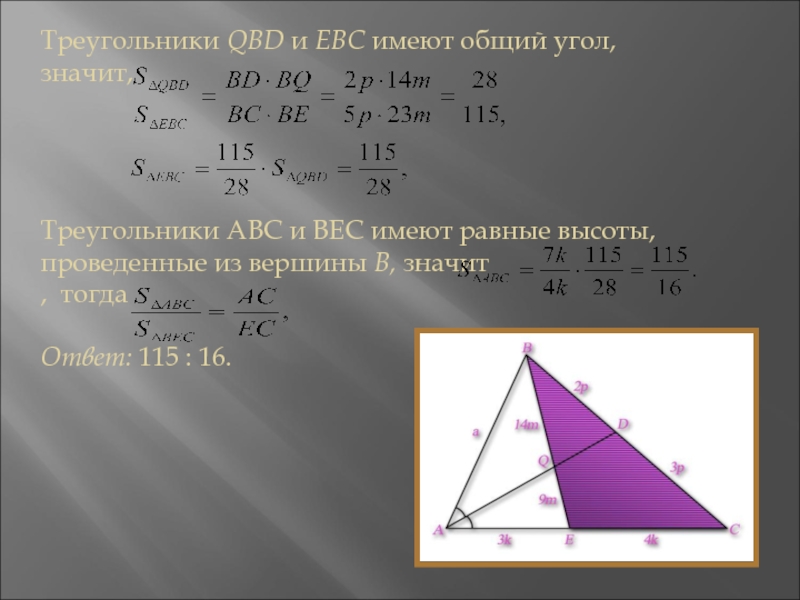
Слайд 13Треугольники QBD и ЕВС имеют общий угол,
значит,
Треугольники ABC и
ВЕС имеют равные высоты, проведенные из вершины В, значит
, тогдаОтвет: 115 : 16.
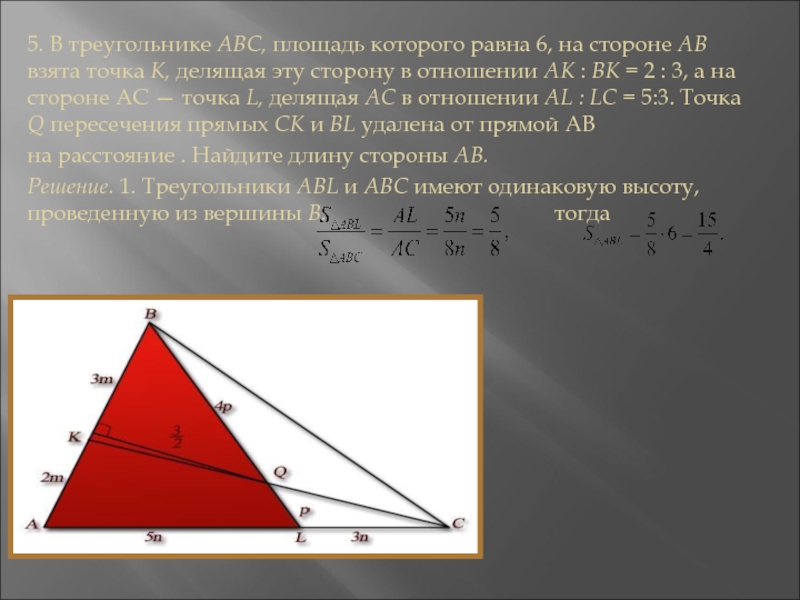
Слайд 145. В треугольнике ABC, площадь которого равна 6, на стороне
АВ взята точка К, делящая эту сторону в отношении АК
: ВК = 2 : 3, а на стороне АС — точка L, делящая АС в отношении AL : LC = 5:3. Точка Q пересечения прямых СК и BL удалена от прямой АВна расстояние . Найдите длину стороны АВ.
Решение. 1. Треугольники ABL и ABC имеют одинаковую высоту, проведенную из вершины В. тогда
Слайд 152. Прямая КС пересекает в треугольнике ABL две стороны и
продолжение третьей. По теореме Менелая
то есть BQ = 4p, QL
= p.3. Треугольники КВQ и ABL имеют общий угол, значит,
Тогда
4.
Тогда
Итак, АВ=4.
Ответ: 4.
Слайд 16Решение задач
по теореме Чевы Джованни
Используя теорему Чевы доказываются следующие утверждения:
1.Медианы
треугольника пересекаются в одной точке.
2.Биссектрисы треугольника пересекаются в одной точке.
3.Высоты
треугольника (или их продолжения) пересекаются в одной точке. 1. Докажите теорему: если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.
Доказательство:
Пусть А1, В1 и С1 – точки касания вписанной окружности треугольника АВС. Для того, чтобы доказать, что отрезки АА1, ВВ1 и СС1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:
Слайд 17Используя свойства касательных, проведенных к окружности из одной точки, введем
обозначения:
Равенство Чевы выполняется, значит, указанные отрезки (биссектрисы треугольника) пересекаются в
одной точке. Эту точку называют точкой Жергонна. Теорема доказана.Слайд 182.Докажите теорему: медианы треугольника пересекаются в одной точке; точка пересечения
делит каждую из них в отношении 2:1, считая от вершины.
Доказательство.
Пусть AL1 ВL2, CL3 — медианы треугольника ABC. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что Тогда по теореме Чевы (обратной) отрезки AL1, ВL2 и СL3 пересекаются в одной точке. Имеем:
Итак, доказано, что медианы треугольника пересекаются в одной точке.
Слайд 192. Пусть О — точка пересечения медиан. Прямая L3С пересекает
две стороны треугольника АВL2 и продолжение третьей стороны этого треугольника.
По теореме МенелаяРассматривая теорему Менелая для треугольников AL C и АL3С, мы получаем, что ,
Теорема доказана.
Слайд 203.Докажите теорему: биссектрисы треугольника пересекаются в одной точке.
Доказательство. Достаточно показать,
что
Тогда по тереме Чевы
(обратной) AL1 BL2, CL3 пересекаются в
одной точке. По свойству биссектрис треугольника:,
Перемножая почленно полученные равенства, получаем
Итак, для биссектрис треугольника равенство
Чевы выполняется, следовательно,
они пересекаются в одной точке.
Теорема доказана.
Слайд 21В заключении
1.Для решения задач необходимо находить треугольник, удовлетворяющий этим теоремам.
2.При
составлении равенства Менелая можно записывать, начиная с любой вершины треугольника,
в любом направлении, а также надо переходить от вершины к вершине через точку пересечения секущей линии с этой стороной или ее продолжением. Заканчивать необходимо в той же вершине с которой начали.3.Утверждения и теоремы, доказанные в курсе планиметрии, можно доказать используя теорему Чевы.
4.В работе размещены задачи, которые были предложены при поступлении в ВУЗы и при проведении олимпиад. Этот материал был изложен на спецкурсе по математике, и может быть использован при подготовке к экзаменам.
Слайд 22Литература
1.Геометрия 7-9 Л.С. Атанасян, В.Ф. Бутузов, Москва, «Просвещение» 1994 г.
2.Математика.
Подготовка к тестированию. Г.Г. Мамонтова, Минск ООО «Новое знание» 2005
г.3. Атанасян Л.С. Бутузов В.Ф.и др.Геометрия: Учеб. пособие для7-9 кл.общеобразоват. учреждений- М.: Просвещение ,1999
4. Балк М. Б. Болтянский В. Г. Геометрия масс -М.: Наука, 1987
5. Балк М. Б. Болтянский В. Г Центр тяжести облегчает решение .стр.32-41 Проложение к журналу КВАНТ №1\95
6. Всероссийские математические олимпиады школьников. -М., Просвещение ,1992
7. Глайзер Г.И. История математики в средней школе .Пособие для учителей .-М.,Просвещение,1970