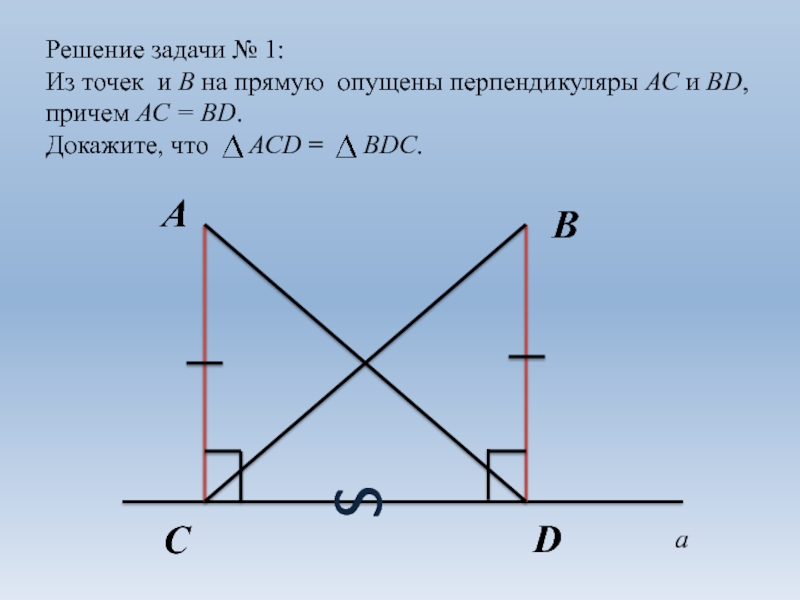
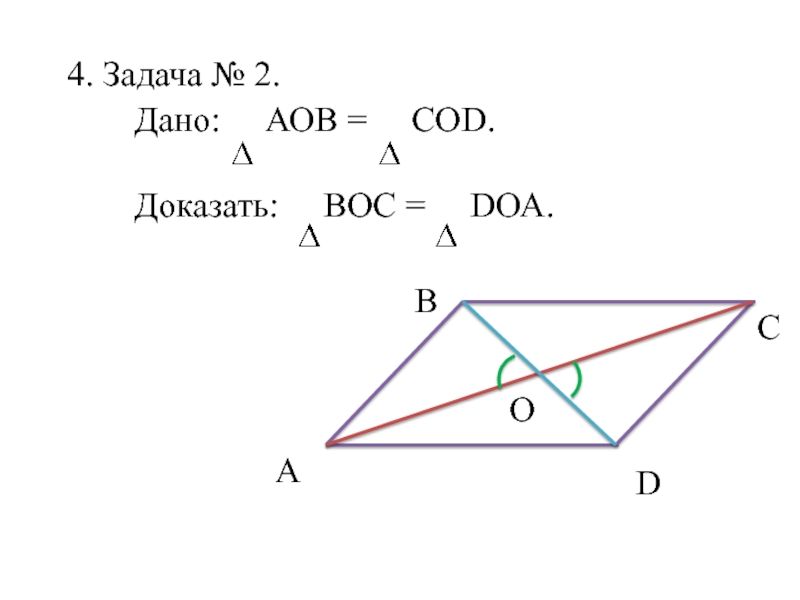
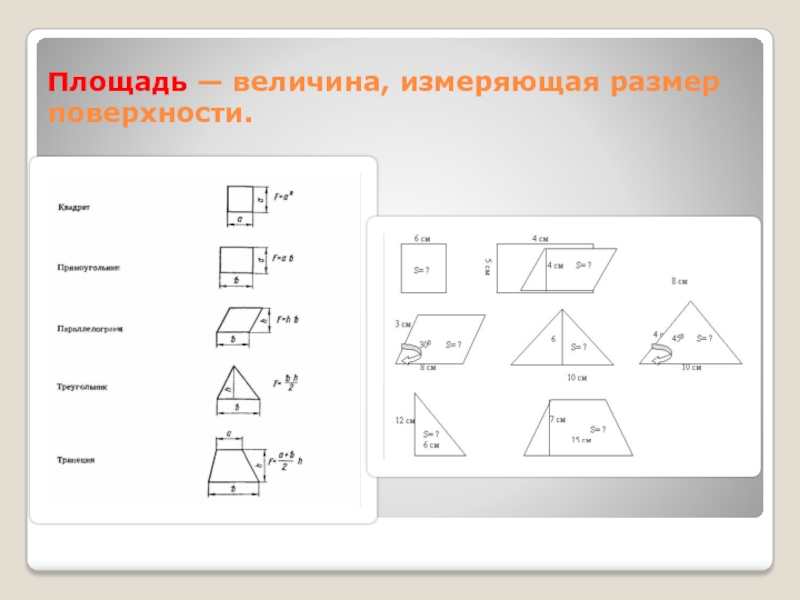
и их свойство.
3. Определение равных фигур, биссектрисы угла.
4. Какой угол
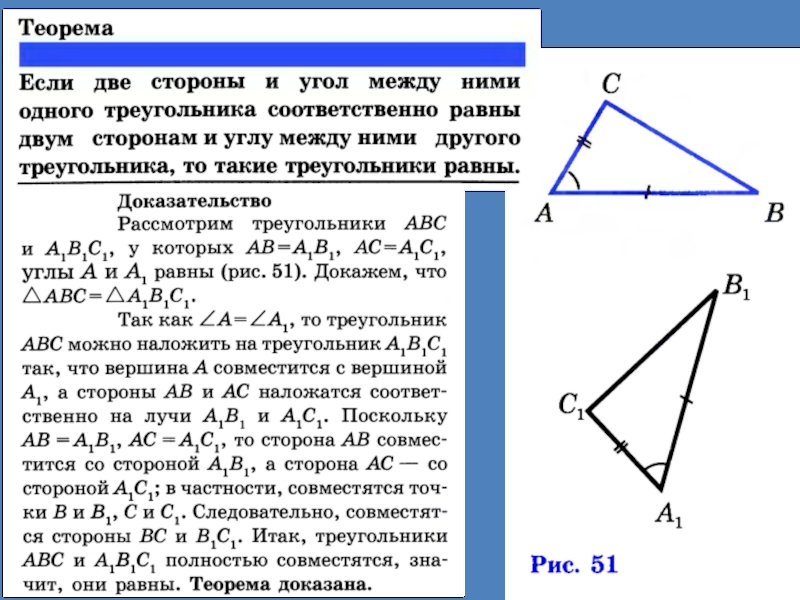
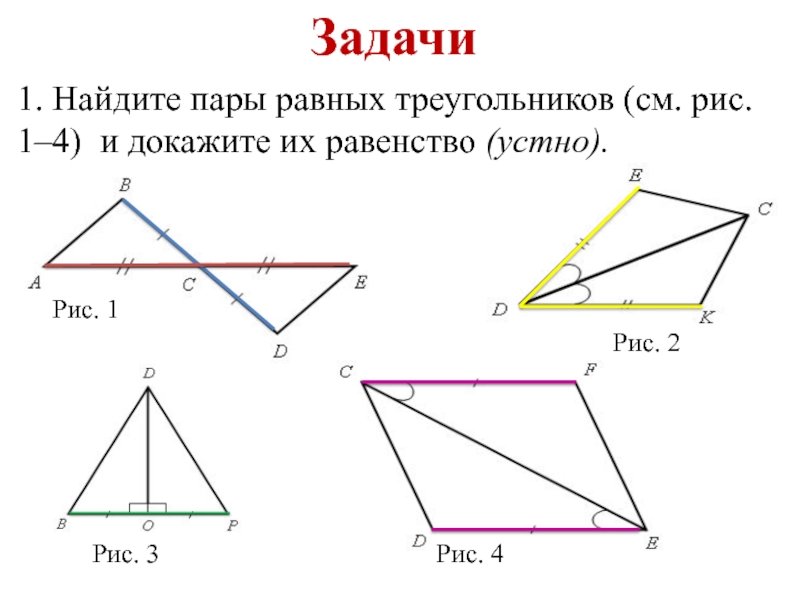
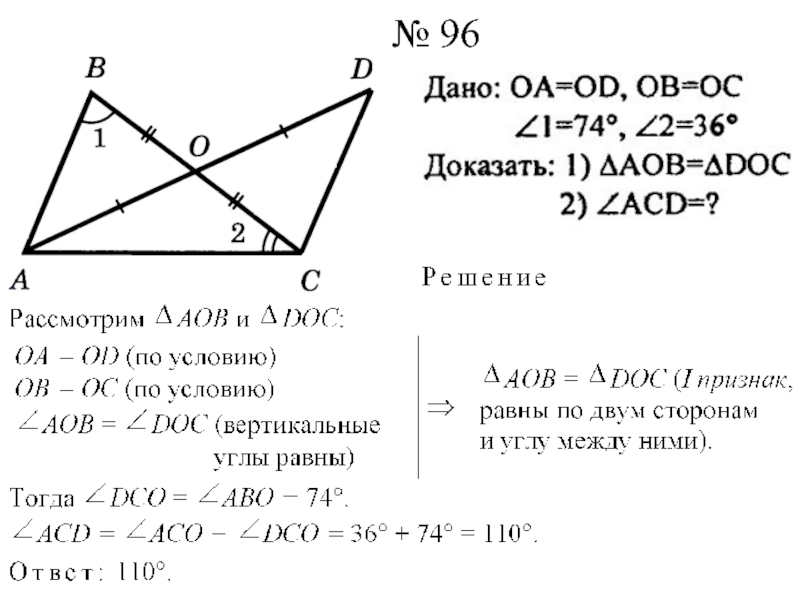
называется острым, прямым, тупым?5. Определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников.