Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники
Содержание
- 1. Треугольники
- 2. АннотацияВ своей работе я рассмотрела сумму углов
- 3. доказательство теоремы о сумме углов треугольника;знакомство с
- 4. Из истории открытияСвойство суммы углов треугольника было
- 5. Сам же Прокл, комментируя первую книгу «Начала»
- 6. А в книге «Начала» Евклида излагается доказательство
- 7. Папирус из Оксиринха Следует
- 8. Аксиома параллельности Евклида, или пятый постулат —
- 9. Постулаты Евклида На современном языке текст
- 10. Вообще у V постулата имеется огромное количество
- 11. Теорема о сумме углов треугольника — классическая теорема
- 12. Доказательство Пусть
- 13. Слайд 13
- 14. Слайд 14
- 15. Сумма углов треугольника в неевклидовой геометрии – геометрии Лобачевского и сферической геометрии
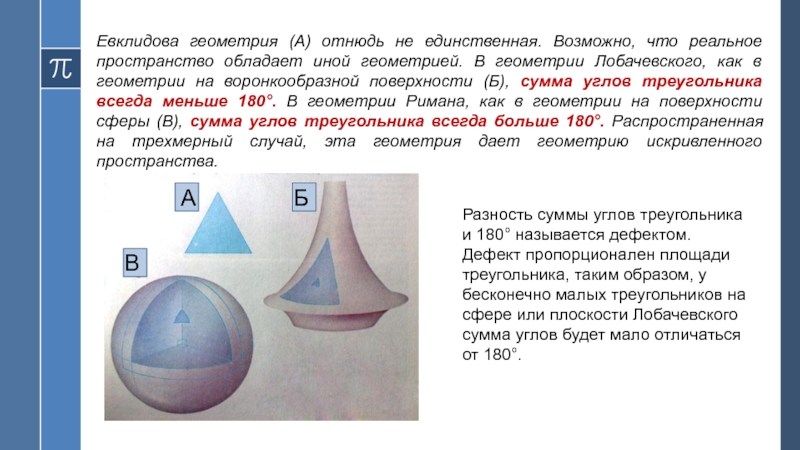
- 16. Евклидова геометрия (А) отнюдь не единственная. Возможно,
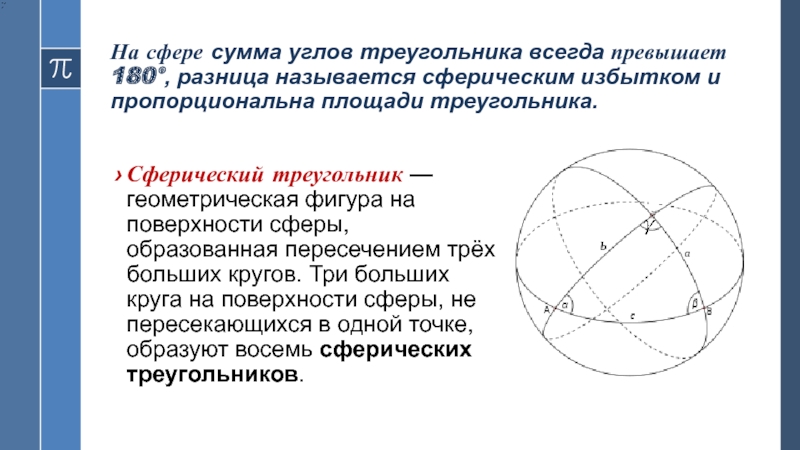
- 17. На сфере сумма углов треугольника всегда превышает
- 18. Сферический треугольникСумма углов сферического треугольника
- 19. У сферического треугольника может быть два прямых
- 20. В плоскости Лобачевского сумма углов треугольника всегда
- 21. Слайд 21
- 22. о применении свойств треугольника - суммы
- 23. о применении свойств треугольника - суммы
- 24. Если сторона треугольника получена из непосредственных измерений,
- 25. В работе «Голландский Эратосфен», опубликованной в
- 26. Триангуляция имеет научное и практическое значениеОна служит
- 27. Как известно, каждая вышка постоянно посылает изменяющийся
- 28. источникиhttp://ru.wikipedia.org/wikihttp://referat.znate.ru/text/index-73500.html?page=3http://bcetyt.ru/computers/notebooks/54051193.html?page=3http://epizodsspace.no-ip.org/bibl/znan/1983/09/09-kosm.htmlhttp://mat.1september.ruБогомолов Н.В., Самойленко П.И. Математика, учебник для
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Краевое государственное бюджетное образовательное учреждение среднего профессионального образования
«Хабаровский судостроительный колледж», Хабаровский край
Мария Борисовна, преподаватель математикиСлайд 2Аннотация
В своей работе я рассмотрела сумму углов треугольника на евклидовой
плоскости и не только. Интерес к этой теме поддерживается тем,
что треугольники часто встречаются в различных явлениях природы, физике, картографии, геодезии, строительстве и в человеческой деятельности, а теорема о сумме углов треугольника используется в геодезии, строительстве и др. областях. Именно это я и рассмотрела в своей работе.Меня заинтересовали разные способы доказательства теоремы о сумме углов треугольника, следствия из этой теоремы. Было интересно узнать – всегда ли сумма углов треугольника равна 1800?
Цели моей работы:
Расширение и углубление знаний о сумме углов треугольника.
Знакомство постулатами Евклида.
Слайд 3доказательство теоремы о сумме углов треугольника;
знакомство с неевклидовыми геометриями –
геометрией Лобачевского и сферической геометрией.
Для достижения этой
цели были в ходе моей деятельности были поставлены и решены следующие задачи.Задачи:
- изучение и анализ учебной, научной и научно-популярной литературы касающейся суммы углов треугольника;
- поиск ответа на вопрос – всегда ли сумма углов треугольника равна 1800?
- развитие интеллектуальных, творческих способностей, математической интуиции, умений анализировать и обобщать;
- приобретение навыков поисковой и исследовательской деятельности;
- приобретение опыта создания презентаций.
Слайд 4Из истории открытия
Свойство суммы углов треугольника было установлено эмпирически, то
есть опытным путем, еще в Древнем Египте. Однако дошедшие до
нас сведения об его доказательствах относятся к более позднему времени.Доказательство, изложенное в современных учебниках, содержится в комментарии Прокла к «Началам» Евклида. Прокл утверждает, что согласно Евдему Родосскому это доказательство было открыто еще пифагорейцами (V в. до н. э.) Прокл пишет: «Пифагор впервые разработал принципы геометрии».
Пифагорейцы содействовали формированию геометрии как науки, основанной на аксиомах и доказательствах.
Евкли́д (ок. 300 г. до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике.
Известен как «Отец Геометрии»
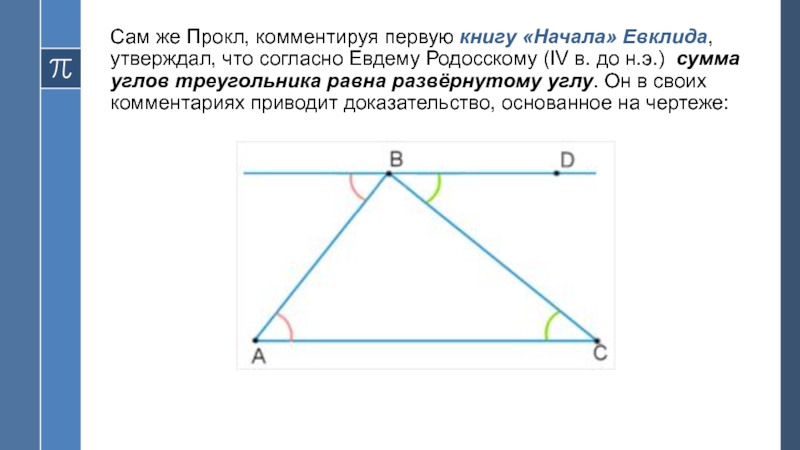
Слайд 5Сам же Прокл, комментируя первую книгу «Начала» Евклида, утверждал, что
согласно Евдему Родосскому (IV в. до н.э.) сумма углов треугольника
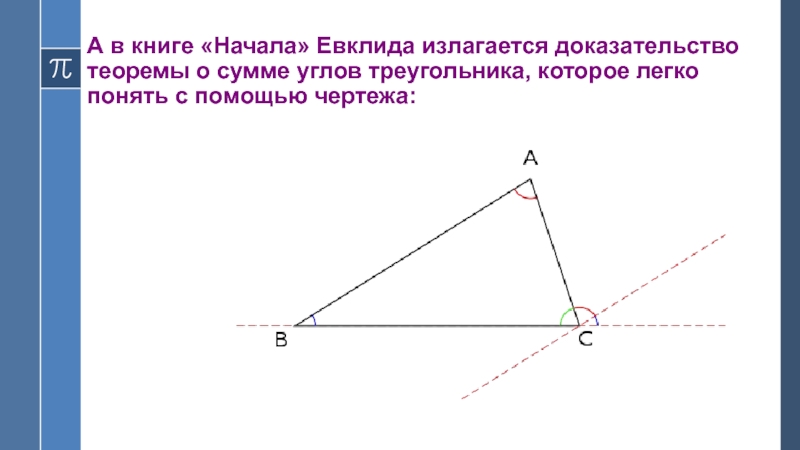
равна развёрнутому углу. Он в своих комментариях приводит доказательство, основанное на чертеже:Слайд 6А в книге «Начала» Евклида излагается доказательство теоремы о сумме
углов треугольника, которое легко понять с помощью чертежа:
Слайд 7Папирус из Оксиринха
Следует отметить, что как доказательство
Прокла, так и доказательство Евклида основываются на том, что при
пересечении двух параллельных прямых третьей внутренние накрест лежащие, а также и соответственные углы равны. Это предложение в свою очередь доказывается при помощи аксиомы параллельности Евклида или пятого постулата Евклида. Итак, теорема о том, что сумма углов треугольника равна 2d, верна, если верна аксиома параллельности Евклида, которая принята в системе аксиом Евклида без доказательства. Наиболее интересен в аксиоматике Евклида последний, знаменитый пятый постулат. Среди других, интуитивно очевидных постулатов, он нарочито чужероден, его громоздкая формулировка закономерно вызывает некоторое чувство протеста и желание отыскать для него доказательство. Такие доказательства уже в древности пытались построить Птолемей и Прокл; а в Новое время из этих попыток развилась неевклидова геометрия – геометрия Лобачевского и сферическая геометрия.
Папирус из Оксиринха
содержащий небольшой фрагмент
«Начал» Евклида
Слайд 8Аксиома параллельности Евклида, или пятый постулат
— одна из аксиом,
лежащих в основании классической планиметрии.
Впервые приведена в «Началах» Евклида.
И
если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.Слайд 9Постулаты Евклида
На современном языке текст Евклида можно переформулировать
так:
Если сумма внутренних углов с общей стороной, образованных
двумя прямыми при пересечении их третьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту же сторону от секущей.Слайд 10Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие
из которых кажутся довольно очевидными. Вот некоторые из них
Существует прямоугольник (хотя бы один), то есть четырёхугольник, у которого все углы прямые. Сумма углов одинакова у всех треугольников.
Существует треугольник, сумма углов которого равна двум прямым.
Вариант: существует, как минимум, одна пара неравновеликих треугольников с одинаковой суммой углов.
Существует треугольник (по меньшей мере один), сумма углов которого равна двум прямым.
Вариант: существует N-угольник, сумма углов которого равна 1800*(N-2).
Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему
Слайд 11Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии. Утверждает,
что
сумма углов треугольника на евклидовой плоскости равна 180°.
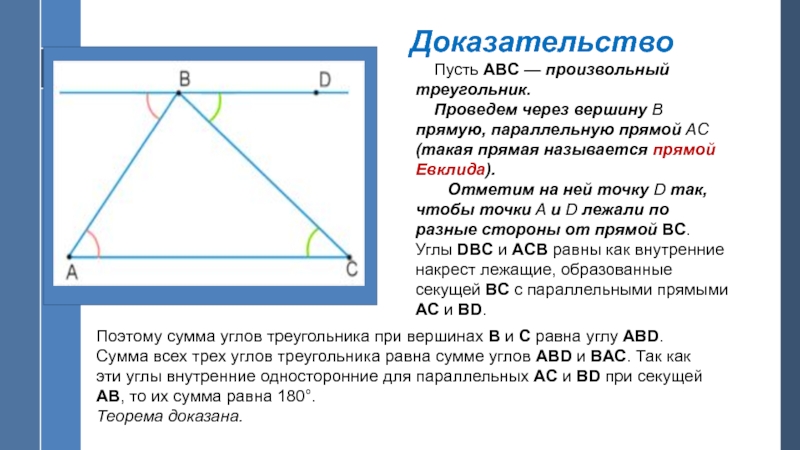
Слайд 12 Доказательство
Пусть ABC — произвольный треугольник.
Проведем через вершину B прямую, параллельную прямой AC (такая прямая
называется прямой Евклида).Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD.
Поэтому сумма углов треугольника при вершинах B и С равна углу ABD. Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°.
Теорема доказана.
Слайд 13
Следствия
Из теоремы следует, что у любого треугольника два угла острые.
Действительно, применяя доказательство от противного, допустим, что у треугольника только
один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.
Слайд 15Сумма углов треугольника в неевклидовой геометрии – геометрии Лобачевского и
сферической геометрии
Слайд 16Евклидова геометрия (А) отнюдь не единственная. Возможно, что реальное пространство обладает
иной геометрией. В геометрии Лобачевского, как в геометрии на воронкообразной поверхности
(Б), сумма углов треугольника всегда меньше 180°. В геометрии Римана, как в геометрии на поверхности сферы (В), сумма углов треугольника всегда больше 180°. Распространенная на трехмерный случай, эта геометрия дает геометрию искривленного пространства.А
В
А
В
Б
Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.
Слайд 17На сфере сумма углов треугольника всегда превышает 180°, разница называется
сферическим избытком и пропорциональна площади треугольника.
Сферический треугольник — геометрическая фигура на
поверхности сферы, образованная пересечением трёх больших кругов. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников.Слайд 18Сферический треугольник
Сумма углов сферического треугольника
всегда меньше и больше
.Величина называется сферическим избытком или сферическим эксцессом.
Если от двух углов сферического треугольника отнимем третий, получим угол, меньший .
В отличие от плоского треугольника, у сферического треугольника может быть два тупых угла или два прямых угла.
Слайд 19У сферического треугольника может быть два прямых угла
Углы сферического треугольника
– это углы между касательными к его сторонам, проведенными в
его вершинах. Как и углы обычного треугольника, они меняются от 0 до 180°. В отличие от плоского треугольника, у сферического сумма углов не равна 180°, а больше: в этом нетрудно убедиться, рассмотрев, например, треугольник, образованный дугами двух меридианов и экватора на глобусе: хотя меридианы сходятся в полюсе, оба они перпендикулярны экватору, а значит, у этого треугольника два прямых угла!Слайд 20В плоскости Лобачевского сумма углов треугольника всегда меньше 180°. Разность
также пропорциональна площади треугольника.
Сумма углов всякого треугольника меньше
и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность где — углы треугольника, пропорциональна его площади: . Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.Модель плоскости Лобачевского – модель Пуанкаре
Слайд 22 о применении свойств треугольника - суммы углов треугольника в
древности
Греческий мудрец Фалес из Милета за шесть веков до
нашей эры определил в Египте высоту пирамиды.
Он воспользовался тенью. Как говорит придание, Фалес избрал день и час, когда длина собственной его тени равнялась его росту, в этот момент высота пирамиды должна также равняться длине отображенной ее тени. Задача греческого мудреца кажется сейчас нам очень простой, но надо помнить, что было это еще за 300 лет до жизни Евклида, который написал книгу, по которой обучаются геометрии до сих пор.
Чтобы измерить высоту пирамиды по ее тени, надо было знать геометрические свойства треугольника:
1) что углы при основании равнобедренного треугольника равны, и обратно - что стороны , лежащие против равных углов треугольника, равны между собой.
2) что сумма углов всякого треугольника равна двум прямым углам (1800).
Только вооруженный этим знанием Фалес вправе был заключить, что когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды ,центр ее основания и конец ее тени должны обозначить равнобедренный треугольник.
(Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно).
Слайд 23 о применении свойств треугольника - суммы углов треугольника в
современной жизни
Метод триангуляции
Теорема о сумме углов треугольника активно «работает» в
геодезии. На ней основан один из методов создания геодезической сети – метод триангуляции ( от лат. triangulum – треугольник).Состоит в построении рядов или сетей примыкающих друг к другу треугольников и в определении положения их вершин в избранной системе координат.
В каждом треугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путём последовательного решения предыдущих треугольников, начиная от того из них, в котором одна из его сторон получена из измерений.
Слайд 24Если сторона треугольника получена из непосредственных измерений, то она называется
базисной стороной триангуляции. Для контроля и повышения точности измеряют большее
число сторон, чем это необходимо.Считается, что метод триангуляции изобрёл и впервые применил В. Снеллиус (математик, физик и астроном) в 1615–17 гг. при прокладке ряда треугольников в Нидерландах для градусных измерений.
Слайд 25 В работе «Голландский Эратосфен», опубликованной в 1617 году, В.
Снеллиус описал метод триангуляции и привел результаты измерений дуги меридиана
между двумя голландскими городами.В России применение этого метода для топографических съемок началось на рубеже XVII XIXвв., а к началуXXв. Он получил повсеместное распространение.
Пример геодезического сигнала
Слайд 26Триангуляция имеет научное и практическое значение
Она служит для:
определения формы
и размеров Земли методом градусных измерений;
изучения горизонтальных движений земной коры;
обоснования
топографических съёмок в различных масштабах и целях;обоснования различных геодезических работ при изыскании;
проектировании и строительстве крупных инженерных сооружений;
при планировке и строительстве городов и т.д.
Слайд 27Как известно, каждая вышка постоянно посылает изменяющийся код, а телефон
принимает его и отсылает обратно. Именно такая схема работы позволяет
автоматически выбирать вышку через которую пойдет сигнал для наилучшего качества связи. Естественно, если вышек несколько, то можно применить метод триангуляции для вычисления точного положения телефона.А еще триангуляция – один из методов вычисления места нахождения абонента мобильной связи. Происходит это путем наложения координат абонента на карту местности
Слайд 28источники
http://ru.wikipedia.org/wiki
http://referat.znate.ru/text/index-73500.html?page=3
http://bcetyt.ru/computers/notebooks/54051193.html?page=3
http://epizodsspace.no-ip.org/bibl/znan/1983/09/09-kosm.html
http://mat.1september.ru
Богомолов Н.В., Самойленко П.И. Математика, учебник для учреждений среднего профессионального
образования. – М., 2009
Богомолов Н.В., Сборник задач по математике, учебник
для учреждений среднего профессионального образования. – М., 2010Богомолов Н.В. Практические занятия по математике. – М. Высшая школа, 2002
Пехлецкий И.Д. Математика: учебник. – М., 2003