Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Треугольники в ЕГЭ по математике ЗАДАЧА № 16
Содержание
- 1. Треугольники в ЕГЭ по математике ЗАДАЧА № 16
- 2. Треугольники в ЕГЭ по математике ЗАДАЧА № 16
- 3. Ключевая задача Доказать, что если медиана, проведенная к гипотенузе, равна ее половине, то треугольник прямоугольный.
- 4. Доказать, что если медиана, проведенная к
- 5. Задача профильного уровня
- 6. АСВ
- 7. АСВ
- 8. Ключевая задачаВычислите длину биссектрисы угла А △АВС
- 9. Вычислите длину биссектрисы угла А △АВС со
- 10. Задача профильного уровня
- 11. вспомним
- 12. Слайд 12
- 13. Слайд 13
- 14. Ключевая задачаНайти медиану прямоугольного треугольника, проведенную из прямого угла, если гипотенуза равна 12.
- 15. Найти медиану прямоугольного треугольника, проведенную из
- 16. Ключевая задачаНайти площадь треугольника, две медианы которого перпендикулярны и равны 3 и 6.
- 17. Найти площадь треугольника, две медианы которого перпендикулярны и равны 3 и 6.
- 18. Задача профильного уровняОкружность с центром в точке
- 19. Окружность с центром в точке О
- 20. Окружность с центром в точке О касается
- 21. Ключевая задача
- 22. Слайд 22
- 23. Ключевая задачаНа отрезке АС, равном 10, взяты
- 24. На отрезке АС, равном 10, взяты точки
- 25. Ключевая задачаНа серединах сторон АВ и ВС
- 26. На серединах сторон АВ и
- 27. Задача профильного уровня
- 28. Слайд 28
- 29. Слайд 29
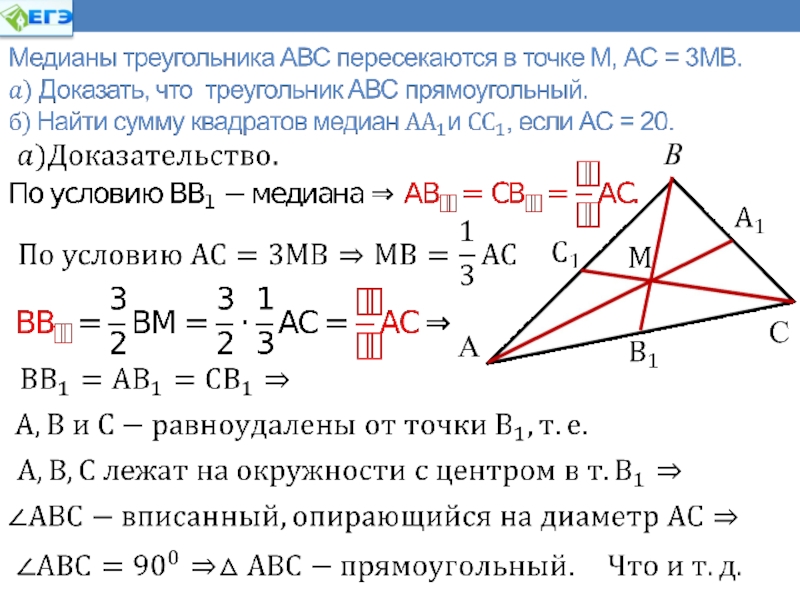
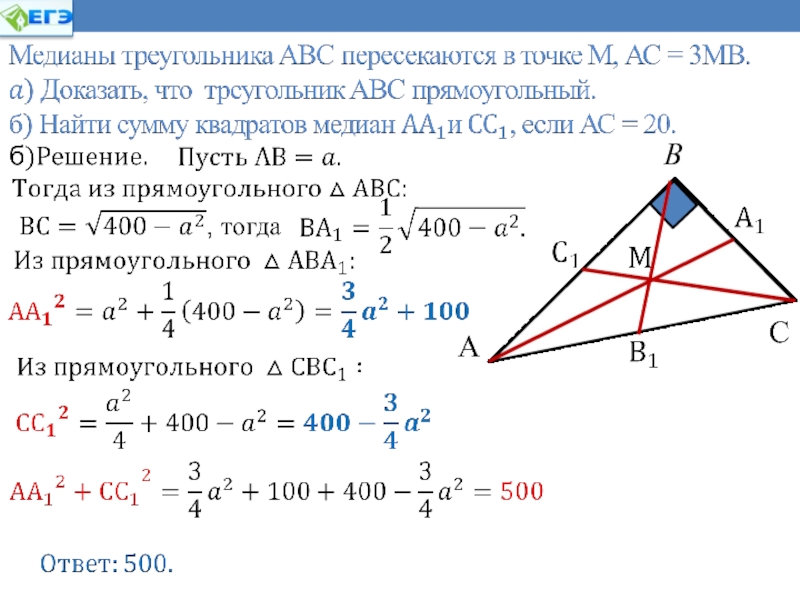
- 30. Ключевая задачаВ треугольнике АВС проведена биссектриса ВМ.
- 31. В треугольнике АВС проведена биссектриса ВМ.
- 32. Ключевая задачаВ треугольнике АВС прямая МК пересекает
- 33. В треугольнике АВС прямая МК пересекает
- 34. Ключевая задача
- 35. 2
- 36. Задача профильного уровня
- 37. Слайд 37
- 38. Слайд 38
- 39. Спасибо за внимание! Удачи на ЕГЭ.
- 40. Вспомним!!!Теорема, обратная теореме Фалеса.Если прямые, пересекающие стороны
- 41. Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Задачи планиметрии
Профильный уровень
Учитель математики
МАОУ «Обдорская гимназия»
г. Салехард ЯНАО
Е.И. Гусак
Слайд 3Ключевая задача
Доказать, что если медиана, проведенная к гипотенузе, равна
ее половине, то треугольник прямоугольный.
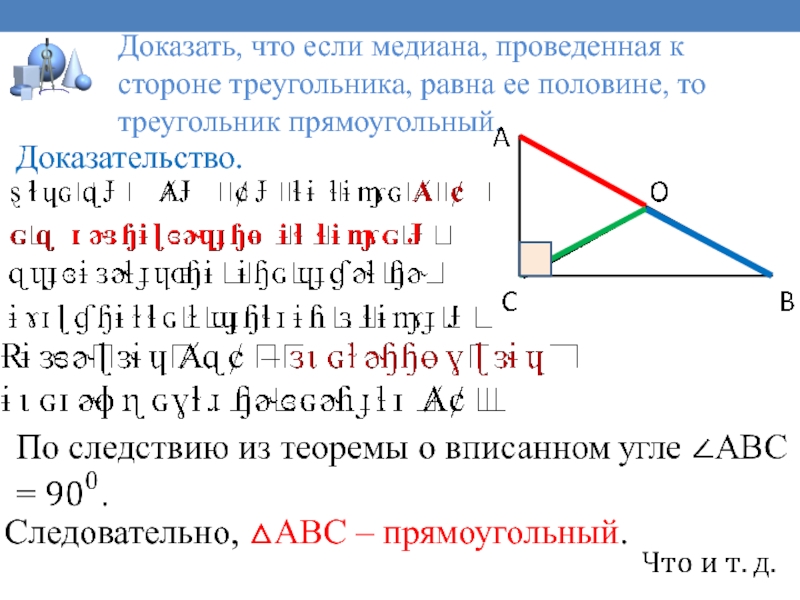
Слайд 4 Доказать, что если медиана, проведенная к стороне треугольника, равна ее
половине, то треугольник прямоугольный.
Доказательство.
Следовательно, △АВС – прямоугольный.
Слайд 8Ключевая задача
Вычислите длину биссектрисы угла А △АВС со сторонами АВ
= 18, ВС = 15, АС = 12.
Слайд 14Ключевая задача
Найти медиану прямоугольного треугольника, проведенную из прямого угла, если
гипотенуза равна 12.
Слайд 15 Найти медиану прямоугольного треугольника, проведенную из прямого угла, если гипотенуза
равна 12.
Решение.По свойству медианы:
медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы.
Следовательно, медиана равна 6.
Ответ: 6.
вспомним
Слайд 16Ключевая задача
Найти площадь треугольника, две медианы которого перпендикулярны и равны
3 и 6.
Слайд 18Задача профильного уровня
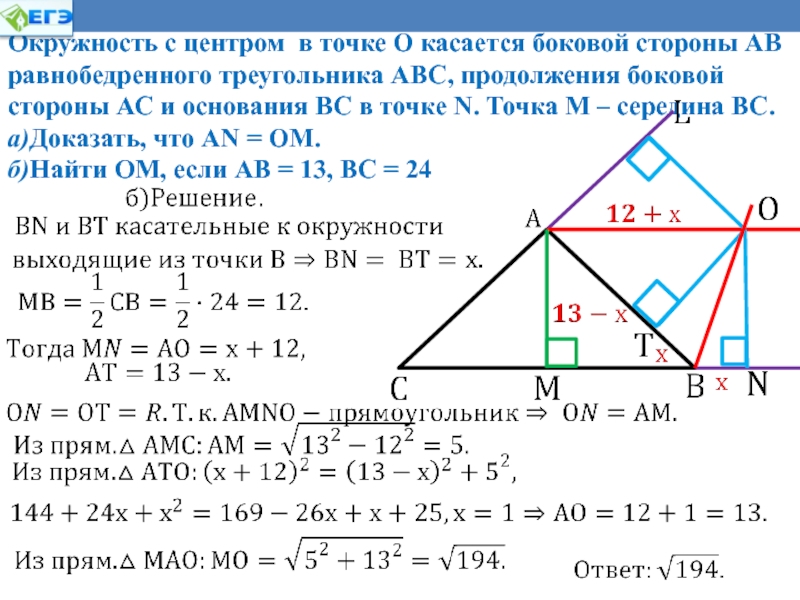
Окружность с центром в точке О касается боковой
стороны АВ равнобедренного треугольника АВС, продолжения боковой стороны АС и
основания ВС в точке N. Точка М – середина ВС.a)Доказать, что AN = ОМ.
б)Найти ОМ, если АВ = 13, ВС = 24.
Слайд 19 Окружность с центром в точке О касается боковой стороны АВ
равнобедренного треугольника АВС, продолжения боковой стороны АС и основания ВС
в точке N. Точка М – середина ВС. a)Доказать, что AN = ОМ. б)Найти ОМ, если АВ = 13, ВС = 24.Слайд 20Окружность с центром в точке О касается боковой стороны АВ
равнобедренного треугольника АВС, продолжения боковой стороны АС и основания ВС
в точке N. Точка М – середина ВС. a)Доказать, что AN = ОМ. б)Найти ОМ, если АВ = 13, ВС = 24Слайд 23Ключевая задача
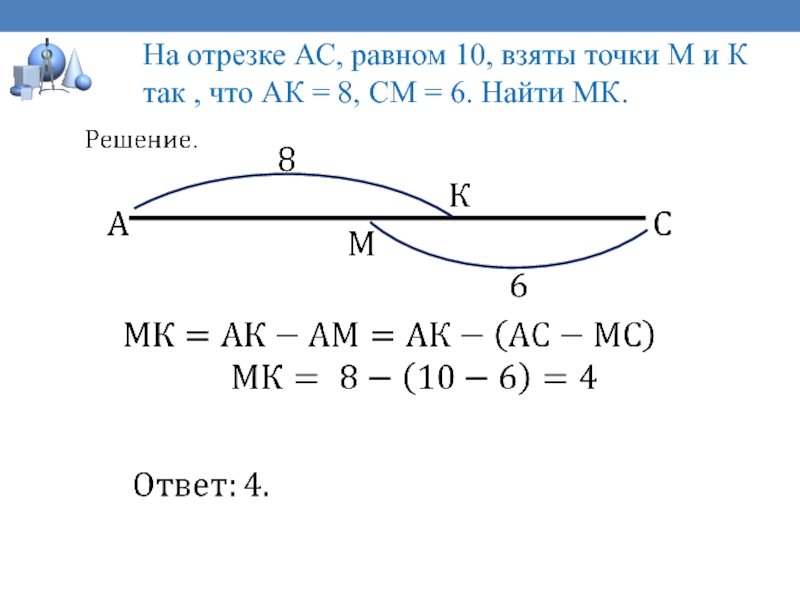
На отрезке АС, равном 10, взяты точки М и
К так , что АК = 8, СМ = 6.
Найти МК.Слайд 25Ключевая задача
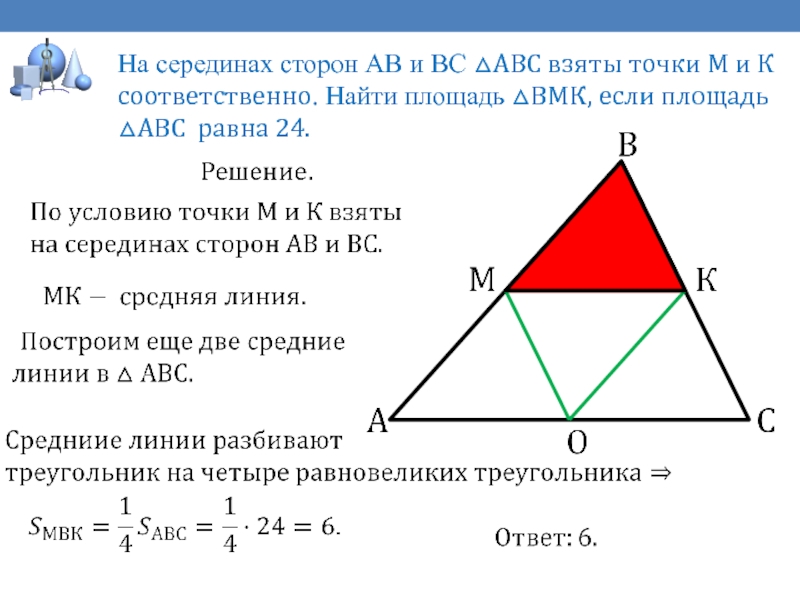
На серединах сторон АВ и ВС △АВС взяты точки
М и К соответственно. Найти площадь △ВМК, если площадь △АВС
равна 24.Слайд 26 На серединах сторон АВ и ВС △АВС взяты точки М
и К соответственно. Найти площадь △ВМК, если площадь △АВС равна
24.Слайд 30Ключевая задача
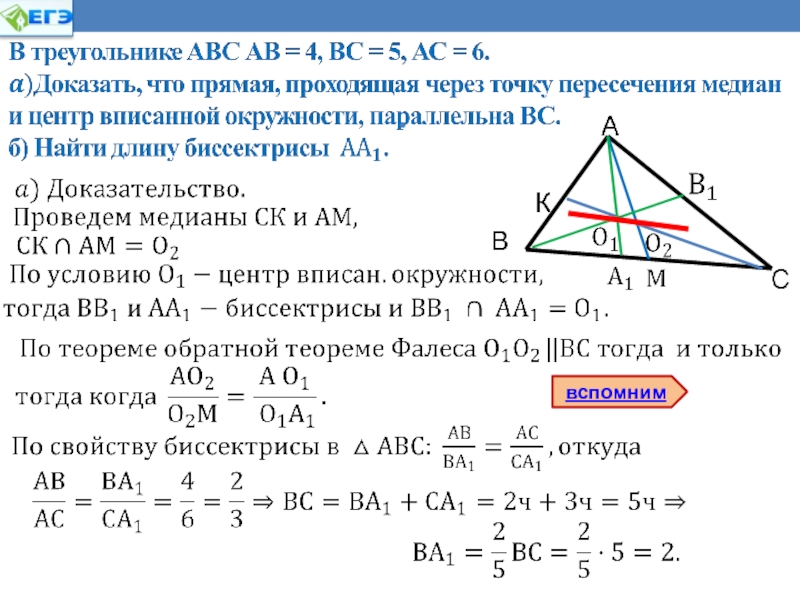
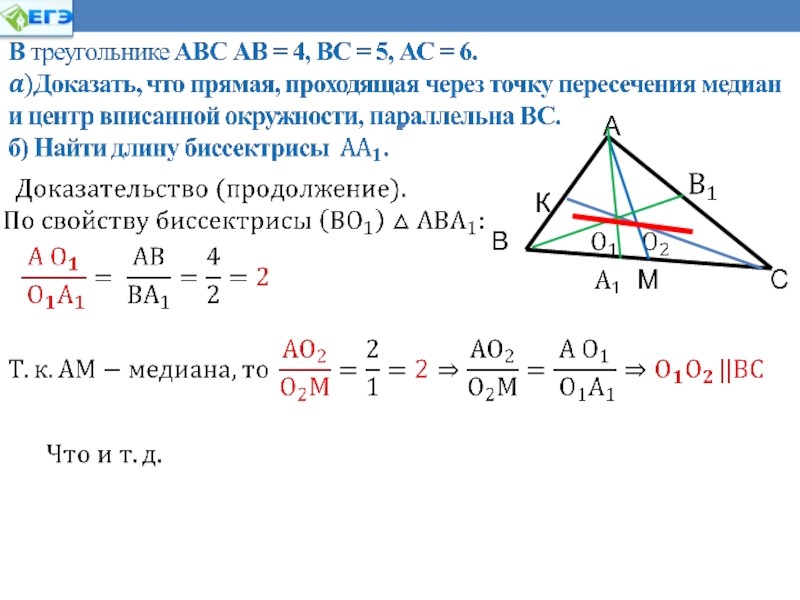
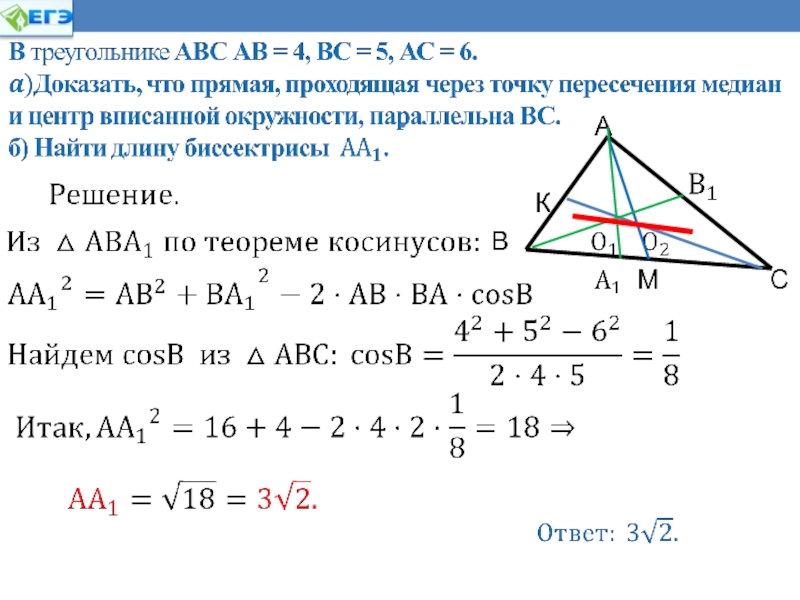
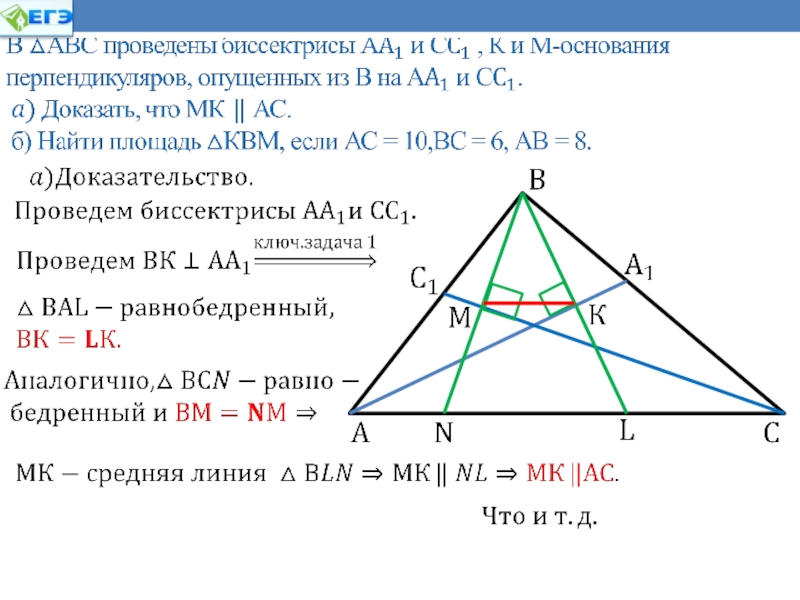
В треугольнике АВС проведена биссектриса ВМ. АВ = 2,
ВС = 3, АС = 3. Найти АМ, МС.
Слайд 32Ключевая задача
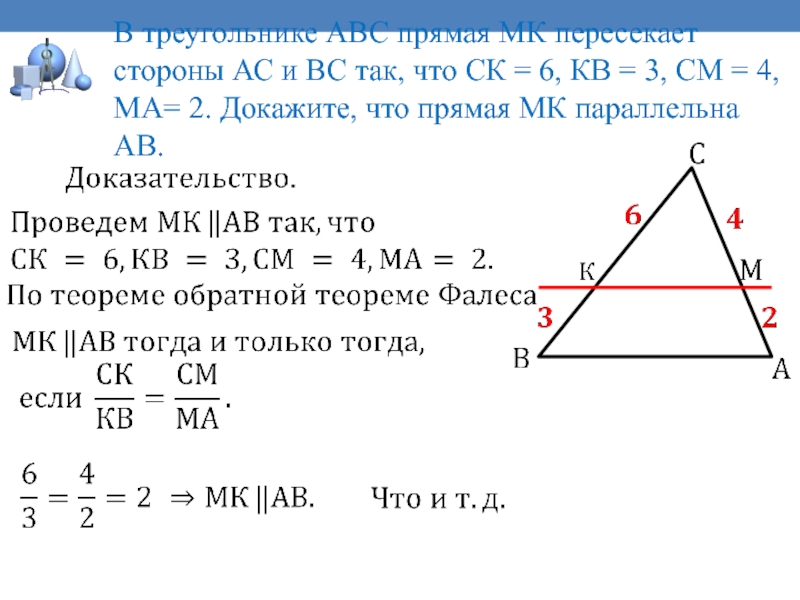
В треугольнике АВС прямая МК пересекает стороны АС и
ВС так, что СК = 6, КВ = 3, СМ
= 4, МА = 2.Докажите, что прямая МК параллельна АВ.
Слайд 33 В треугольнике АВС прямая МК пересекает стороны АС и ВС
так, что СК = 6, КВ = 3, СМ =
4, МА= 2. Докажите, что прямая МК параллельна АВ.Слайд 40Вспомним!!!
Теорема, обратная теореме Фалеса.
Если прямые, пересекающие стороны угла, отсекают на
одной и на другой стороне угла равные (или пропорциональные) между
собой отрезки, начиная от вершины, то такие прямые параллельны.В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
назад
Слайд 41Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы
1) В прямоугольном
△ АВС из вершины прямого угла С проведем к гипотенузе
AB отрезок CO так, чтобы CO=OA.2) ∆ AOC — равнобедренный с основанием AC ⇒ ∠OAC=∠OCA=α.
3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в △АВС ∠B=90º- α.
4) Так как ∠BCA=90º (по условию), то ∠BCO=90º- ∠OCA=90º-α.
5) Рассмотрим треугольник BOC.
∠BCO=90º-α, ∠B=90º- α, следовательно, ∠BCO=∠B ⇒ BOC — равнобедренный с основанием BC. Отсюда BO=CO.
назад