Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольная система координат в пространстве. Координаты вектора
Содержание
- 1. Прямоугольная система координат в пространстве. Координаты вектора
- 2. Прямоугольная система координатЕсли через точку пространства проведены
- 3. Прямые, с выбранными на них направлениями, называются
- 4. Прямоугольная система координатВся система координат обозначается Охуz.
- 5. Точка О разделяет каждую из осей координат
- 6. В прямоугольной системе координат каждой точке М
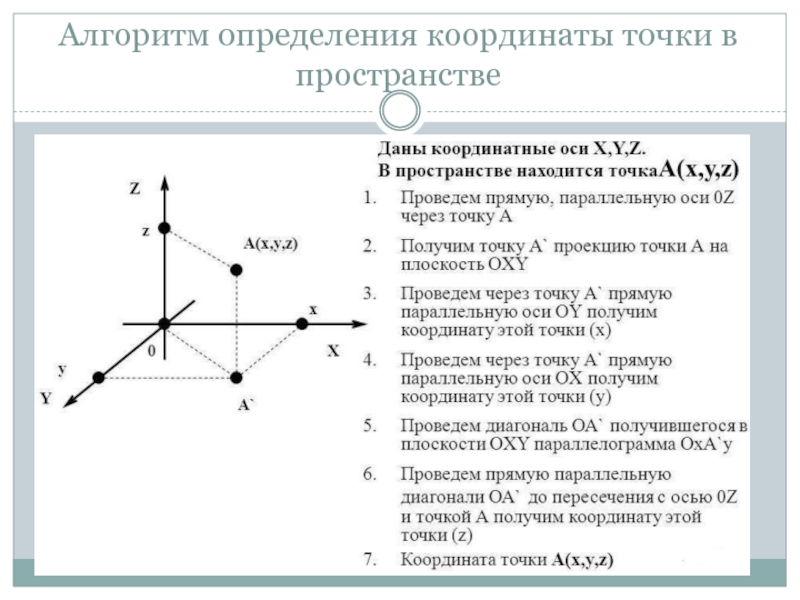
- 7. Алгоритм определения координаты точки в пространстве
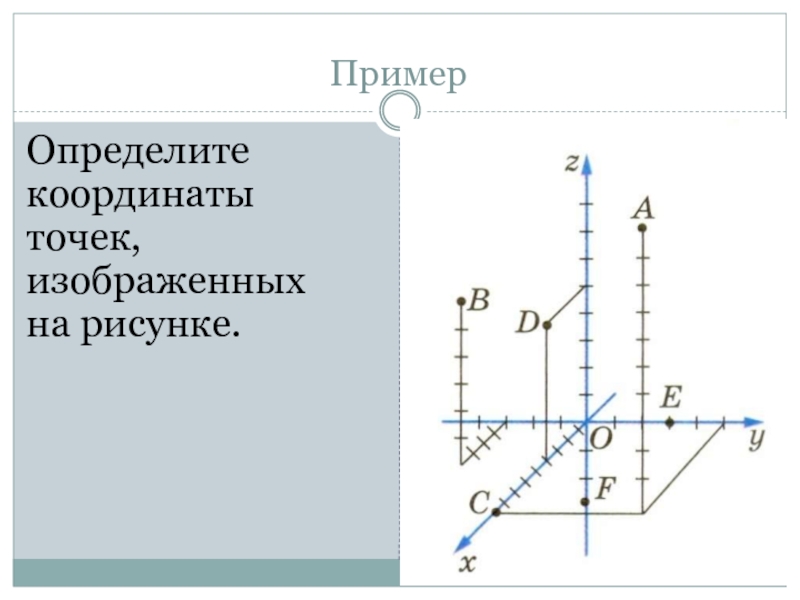
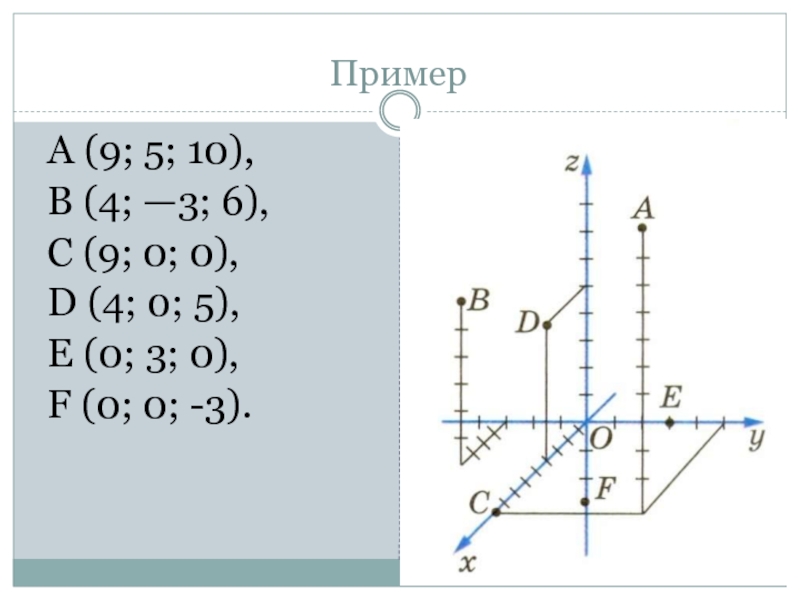
- 8. Определите координаты точек, изображенных на рисунке.Пример
- 9. А (9; 5; 10), В (4; —3;
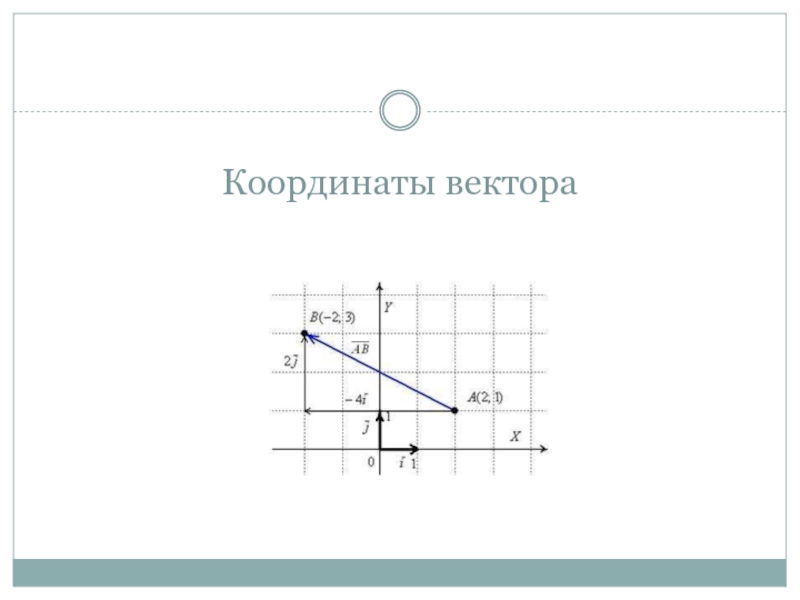
- 10. Координаты вектора
- 11. Что такое вектор?Вектором называется направленный отрезок, для которого указано
- 12. Любой вектор можно разложить
- 13. Коэффициенты х, у и z в разложении
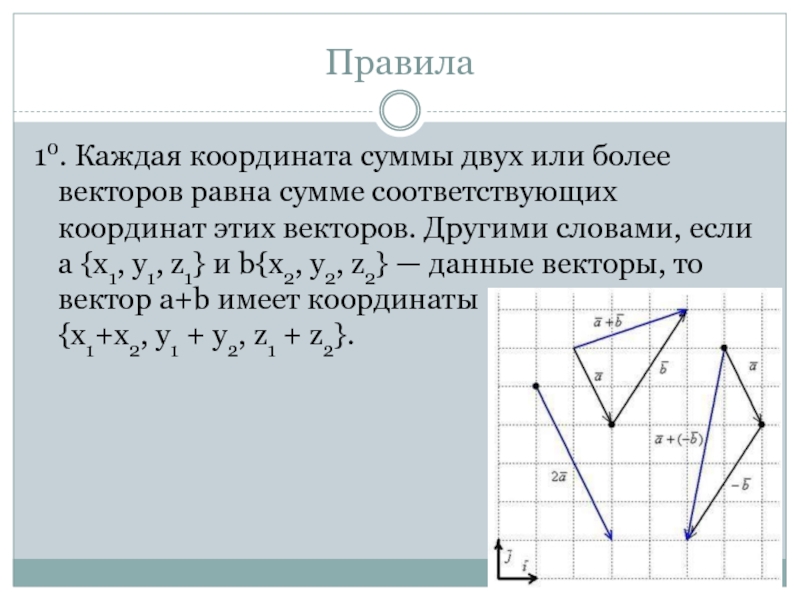
- 14. Правила10. Каждая координата суммы двух или более
- 15. Правила20. Каждая координата разности двух векторов равна
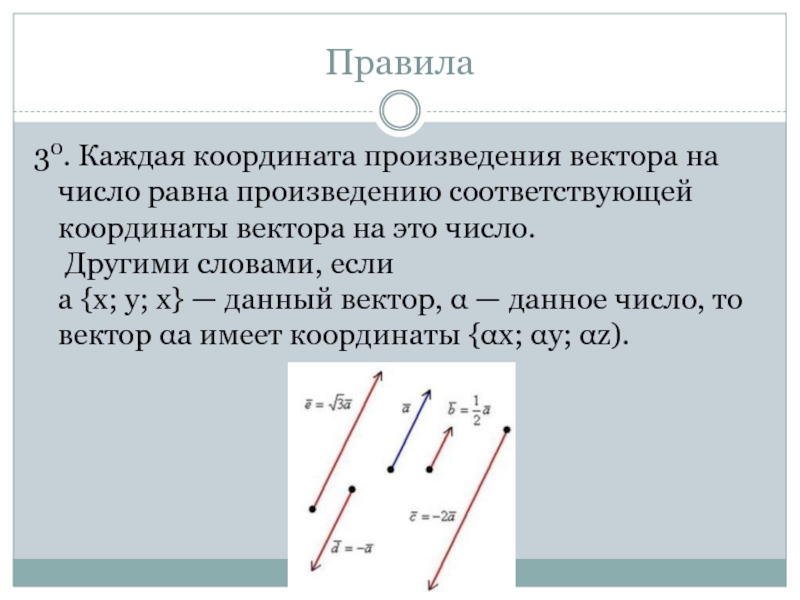
- 16. Правила30. Каждая координата произведения вектора на число
- 17. Скачать презентанцию
Прямоугольная система координатЕсли через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве
Слайды и текст этой презентации
Слайд 1Преподаватель ГАПОУ РО «РКТМ»
Колыхалина К.А.
Прямоугольная система координат в пространстве.
Координаты вектора
Слайд 2Прямоугольная система координат
Если через точку пространства проведены три попарно перпендикулярные
прямые, на каждой из них выбрано направление и выбрана единица
измерения отрезков, то говорят, что задана прямоугольная система координат в пространствеСлайд 3Прямые, с выбранными на них направлениями, называются осями координат, а
их общая точка — началом координат. Она обозначается обычно буквой
О. Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат.Прямоугольная система координат
Слайд 4Прямоугольная система координат
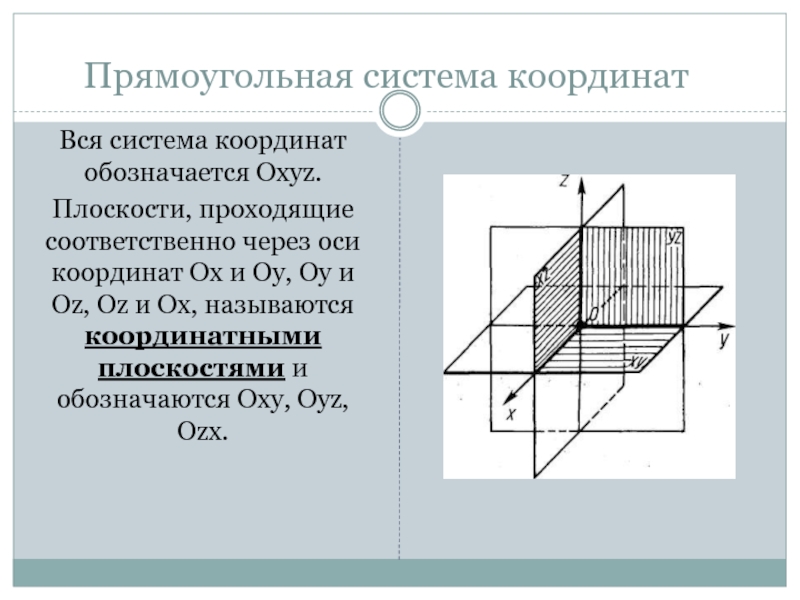
Вся система координат обозначается Охуz.
Плоскости, проходящие соответственно
через оси координат Ох и Оу, Оу и Оz, Оz
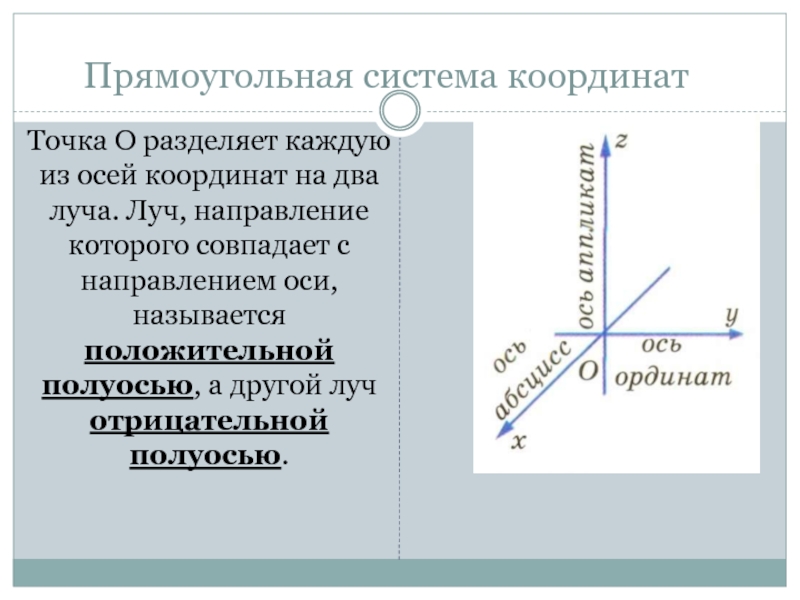
и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.Слайд 5Точка О разделяет каждую из осей координат на два луча.
Луч, направление которого совпадает с направлением оси, называется положительной полуосью,
а другой луч отрицательной полуосью.Прямоугольная система координат
Слайд 6В прямоугольной системе координат каждой точке М пространства сопоставляется тройка
чисел, которые называются ее координатами.
Прямоугольная система координат
Слайд 11Что такое вектор?
Вектором называется направленный отрезок, для которого указано его начало и
конец.
В данном случае началом отрезка является точка A, концом отрезка –
точка B. Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери колледжа или выйти из дверей колледжа – это совершенно разные вещи.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.