Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История возникновения счета и простейших счетных приборов
Содержание
- 1. История возникновения счета и простейших счетных приборов
- 2. На протяжении всей своей жизни люди сталкиваются
- 3. познакомиться с историей возникновения
- 4. Факты убедительно свидетельствуют о том,
- 5. На этой кости тридцать тысяч лет назад
- 6. КипуC помощью узелков в государстве инков
- 7. С усложнением хозяйственной деятельности
- 8. Абаком называлась дощечка покрытая
- 9. Китайская разновидность абака - суаньпань - появилась
- 10. «Счет на линиях»Заменил в Средние века в
- 11. Дощаный счет Один из ранних образцов такого
- 12. Арифметическая машина ( или Паскалево колесо) была
- 13. Модель счетного устройства Леонардо да Винчи Арифмометр
- 14. В 1834 году англичанин Чарльз Бэббидж изобретает
- 15. Индийская или арабская нумерация
- 16. Индийская или арабская нумерация Это,
- 17. Вавилонская нумерация = 5 =30
- 18. Древнегреческая нумерацияВ Греции
- 19. Древнеегипетская нумерация
- 20. К примеру, запись числа 1.124.624 выглядела следующим
- 21. Нумерация племени МайяЭта нумерация очень интересна тем,
- 22. Римская (латинская) нумерацияДревние
- 23. Славянская глаголическая нумерацияЭта нумерация была создана для
- 24. Славянская кириллическая нумерацияЮжные и восточные славянские
- 25. Китайская нумерацияЭта нумерация одна из
- 26. Проследив основные этапы
- 27. http://ru.wikipedia.org/wiki/История_математикиИнформационные источники http://irnik.narod.ru/htm/histori.htm http://freecode.pspo.perm.ru/436/work/ss/ist_ch.htm http://www.sch297.ru/projects/ivt
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Автор:
Кудряшова Любовь Александровна,
учитель математики
МОУ СОШ № 9 г. Переславль-Залесский, 2010
История
возникновения счета и простейших счетных приборов
Слайд 2На протяжении всей своей жизни люди сталкиваются с числами и
выполняют над ними арифметические действия. Мы воспринимаем это, как факт,
как само собой разумеющееся. Действительно, мы спокойно пересчитываем предметы, даем этому множеству количественную характеристику , даже не задумываясь о том, что и в далеки времена наши предки, которые долгое время общались жестами и членораздельными звуками, могли считать или, во всяком случае, могли определить количество предметов. Нас очень заинтересовало, на какой же стадии развития человека зародился счет, как люди «укрощали» эту науку.Слайд 3 познакомиться с историей возникновения счета разных
народов стран
познакомиться с простейшими счётными
приборамиЦель
Слайд 4Факты убедительно свидетельствуют о том, что счет
возник раньше, чем названия чисел. Человек пользовался окружавшими его
однотипными предметами счета: пальцы, камешки, узелки, нарисованные на стене черточки, зарубки на палках и на деревьях, кучки камней.Счётные приборы
Слайд 5На этой кости тридцать тысяч лет назад сделаны
нарезки, они показывают, что уже
тогда наши предки умели не только считать, но и записывать результаты счета.Кость из Ля Ферраси
(50 тыс. лет до н.э.)
Считается, что правильно расположенные линии использовались для счета
Браслеты из бивня мамонта (30–25 тыс. лет до н.э. ) Число черточек на пластинках показывает, что владельцы браслетов знали счет до 20(число пальцев на руках и ногах).
Слайд 6Кипу
C помощью узелков в государстве инков записывали результаты
счета, и исторические события.
Бирки (40–12 тыс. лет до
н.э.)Кости или палочки с насечками. Использовались для записи результатов счета.
Слайд 7С усложнением хозяйственной деятельности людей
понадобилось вести счет в более обширных пределах, что потребовало создания
более сложных счётных устройств. Это различные счёты(абак, соробан, суан-пан) и позднее в средние века появляются механические счётные устройства: машина Паскаля, машина Лейбница, логарифмические линейки. Далее разрабатываются счётные устройства, которые могут работать под управлением программы - разносная и аналитическая машины Бэббиджа.Слайд 8 Абаком называлась дощечка покрытая слоем пыли,
на которой острой палочкой проводились линии и какие-нибудь предметы,
размещавшиеся в полученных колонках по позиционному принципу. Изготовлялся абак из бронзы, камня, слоновой кости и цветного стекла. До нашего времени дошёл бронзовый римский абак, на котором камешки передвигались в вертикально прорезанных желобках. Внизу помещались камешки для счета до пяти, а в верхней части имелось отделение для камешка, соответствующего пятёрке.
Слайд 9Китайская разновидность абака - суаньпань - появилась в VI веке
н.э.. Суаньпань представляет собой прямоугольную раму, в которой
параллельно друг другу протянуты проволоки или веревки числом от девяти и более; перпендикулярно этому направлению суаньпань перегорожен на две неравные части. В большом отделении(«земля») на каждой проволоке нанизано по пять шариков, в меньшем («небо») - по два. Проволокисоответствуют десятичным разрядам.
Слайд 10«Счет на линиях»
Заменил в Средние века в Европе абак. Русским
аналогом был «счет костьми » .
Использовались разлинованная таблица и жетоны. Был вытеснен выкладками на бумаге.«Сошный счет»
Специальный прибор для вычисления поземельного податного обложения в России XV – XVI вв. Предусматривал умножение на коэффициент и работу с дробями
Слайд 11Дощаный счет
Один из ранних образцов такого "счета" представлял собой
два соединенных ящика, одинаково разделенных по высоте перегородками. В каждом
ящике два счетных поля с натянутыми веревками или проволочками. На верхних 10 веревках по 9 косточек (четок), на 11-й их четыре, на остальных веревках - по одной.Соробан
Соробан - японский абак , происходит от китайского суаньпаня, который был завезен в Японию в XV- XVI веках. Соробан проще своего предшественника , у него на "небе" на один шарик меньше, чем у суаньпаня
Слайд 12Арифметическая машина ( или Паскалево колесо) была готова в 1645
году. В отличие от известных счетных инструментов типа абака в
арифметической машине вместо предметного представления чисел использовалось их представление в виде углового положения оси (вала) или колеса, которое несет эта ось.Суммирующая машина Блеза Паскаля. Первая дошедшая до нас механическая вычислительная машина. Изготовлена Паскалем в 1642 г. в 19 лет, когда он уже был известен, как математик.
Слайд 13Модель счетного устройства Леонардо да Винчи
Арифмометр Лейбница.
Первое
устройство, предназначенное для выполнения не только сложения и вычитания, но
и умножения и деления. Изобретено Готфридом Лейбницем в 1673 г.13 - разрядное суммирующее устройство с десятизубыми колёсами. В рекламных целях оно было воспроизведено фирмой IBM и оказалось вполне работоспособным
Слайд 14В 1834 году англичанин Чарльз Бэббидж изобретает аналитическую машину. Она
состояла из «склада» для хранения чисел ( накопитель), «мельницы» -
для производства арифметических действий над числами ( арифметическое устройство), устройство, управляющее в определенной последовательности операциями машины ( устройство управления ), устройство ввода и вывода данных.Петербургским инженером В. Т. Однером был создан арифмометр, который распространился во всем мире, с его появлением зародилось математическое машиностроение, в течение многих десятков лет он был самой распространенной вычислительной машиной. Только распространение электронных калькуляторов вытеснило арифмометр Однера из всеобщего употребления.
Слайд 15 Индийская или арабская нумерация
Вавилонская нумерация
Древнегреческая нумерация
Древнеегипетская нумерация
Нумерация племени Майя
Римская (латинская) нумерацияСлавянская глаголическая нумерация
Славянская кириллическая нумерация
Китайская нумерация
Письменная нумерация у древних народов
Слайд 16Индийская или арабская нумерация
Это, самая
распространенная на сегодняшний день нумерация. Название «
арабская» для нее не совсем верно, поскольку хоть и завезли ее в Европуиз арабских стран, но там она тоже была не родной. Настоящая родина этой нумерации - Индия.
Первоначально этими знаками представлялись числа 1, 2, 3, ... 9, 10, 20, ..., 90, 100, 1000; с их помощью записывались другие числа. Но в последствии был введен особый знак - жирная точка, или кружок, для указания пустующего разряда; и нумерация «Деванагари» превратилась в поместную десятичную систему.
Слайд 17Вавилонская нумерация
= 5
=30
=35
=59
Запись вавилонской клинописью
чисел, больших 60
= 302 (5x60+2)
= 1295 (21x60+35)
= 3725
(1x60x60+2x60+5)= 7203 (2x60x60+0x60+3)
Числа, меньшие 60, обозначались с помощью двух знаков: единицы и для десятка . Они имели клинообразный вид, так как вавилоняне писали на глиняных дощечках палочками треугольной формы. Эти знаки повторялись нужное число раз. При отсутствии промежуточного разряда применялся знак.
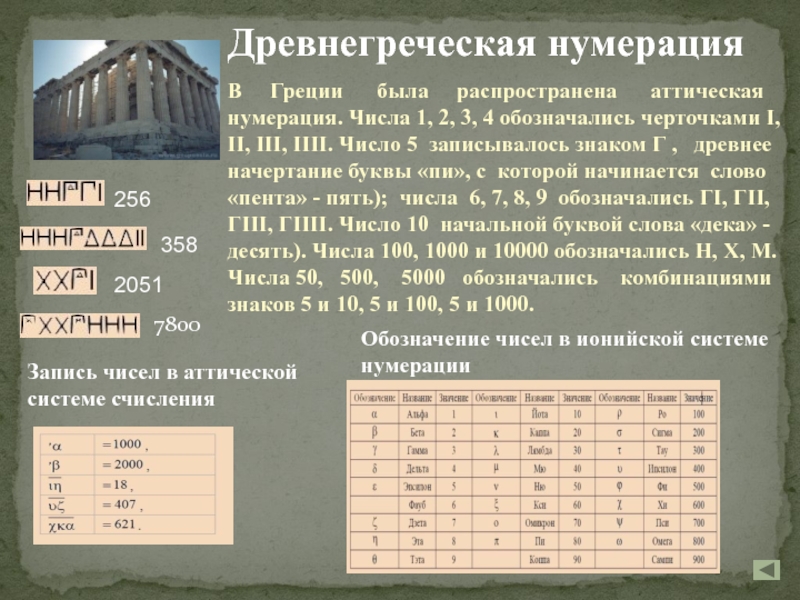
Слайд 18Древнегреческая нумерация
В Греции была
распространена аттическая нумерация. Числа 1, 2, 3, 4
обозначались черточками I, II, III, IIII. Число 5 записывалось знаком Г , древнее начертание буквы «пи», с которой начинается слово «пента» - пять); числа 6, 7, 8, 9 обозначались ГI, ГII, ГIII, ГIIII. Число 10 начальной буквой слова «дека» - десять). Числа 100, 1000 и 10000 обозначались H, X, M. Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000.Запись чисел в аттической системе счисления
256
358
2051
7800
Обозначение чисел в ионийской системе нумерации
Слайд 19Древнеегипетская нумерация
Система счета древних египтян насчитывает семь знаков, передающих разряды чисел. Запись цифр внутри каждого из разрядов производилась
простым увеличением количества знаков по принципу сложения. Например, число «1» передавалось одной чертой (I), «2»- двумя (II), «3» - тремя (III).... «8» - восемью (IIIIIIII), «9» - девятью (IIIIIIIII). Числа, содержащие несколько разрядов единиц, записывались по такому же принципу;
при этом единицы высших разрядов выносились
в начало записи.
Слайд 20К примеру, запись числа 1.124.624 выглядела следующим образом:
В последующие
эпохи он переводится
как «множество». Для обозначения чисел высших разрядов египтяне использовали запись умножения.Слайд 21Нумерация племени Майя
Эта нумерация очень интересна тем, что на ее
развитие не повлияла ни одна из цивилизаций Старого Света.
Сначала эта нумерация обслуживала пятеричную систему счисления, а потом ее приспособили для двадцатеричной. Также большой вес имеют пиктографические знаки, часто изображающиеся со многими деталями животных, людей, частей тела и предметов быта. Истоки лежат в методе счёта, при котором применялись не только десять пальцев рук, но и десять пальцев ног. Также интересным является тот факт, что у майя существовало обозначение нуля, который схематически был представлен в виде пустой раковины от устрицы или улитки. Обозначение нуля также применялось для обозначения бесконечности.Слайд 22
Римская (латинская) нумерация
Древние римляне пользовались «римской
нумерацией». Мы пользуемся для обозначения веков, юбилейных дат, наименования конференций,
для нумерации глав книги или строф стихотворения.В позднейшем своем виде римские цифры выглядят так: I=1, V=5, X=10, L=100, D=500, M=1000.
Запись чисел римскими цифрами:
XXVIII = 28, XXXIX = 39, CCCXCVII = 397, MDCCCXVIII = 1818.
Слайд 23Славянская глаголическая нумерация
Эта нумерация была создана для переписки чисел в
священных книгах западных славян. Использовалась она нечасто, но достаточно долго.
По организации она в точности повторяет греческую нумерацию. Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали Такая запись числа аддитивная, то есть в ней используется только сложение:= 800+60+3 = 863
Для того, чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.
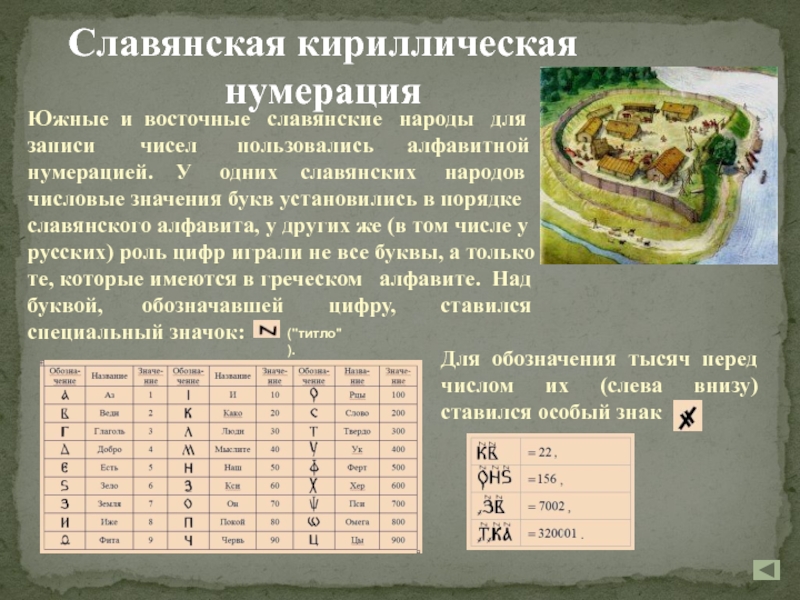
Слайд 24Славянская кириллическая нумерация
Южные и восточные славянские народы
для записи чисел пользовались
алфавитной нумерацией. У одних славянских народов числовые значения букв установились в порядке славянского алфавита, у других же (в том числе у русских) роль цифр играли не все буквы, а только те, которые имеются в греческом алфавите. Над буквой, обозначавшей цифру, ставился специальный значок: ("титло").
Для обозначения тысяч перед числом их (слева внизу) ставился особый знак
Слайд 25Китайская нумерация
Эта нумерация одна из старейших и
самых прогрессивных, поскольку в нее заложены такие же принципы,
как и в современную арабскую, которой мы с Вами пользуемся. Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае.Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого - то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду.
Слайд 26 Проследив основные этапы зарождения чисел,
их различных систем записей у разных народов, необходимо сделать
такой вывод: не зря многие ученые умы интересовались понятием числа, раскрывали его тайны.Да и в наш технократичный век, когда с числами сталкиваешься повсеместно ( на денежных знаках, ценниках, компьютерах, панелях стиральных машин )
это понятие не утратило своей актуальности. Трудно себе представить, как современный человек смог бы прожить, если бы когда-то, много тысячелетий назад, не была бы приоткрыта тайна великих и загадочных чисел.
Вывод