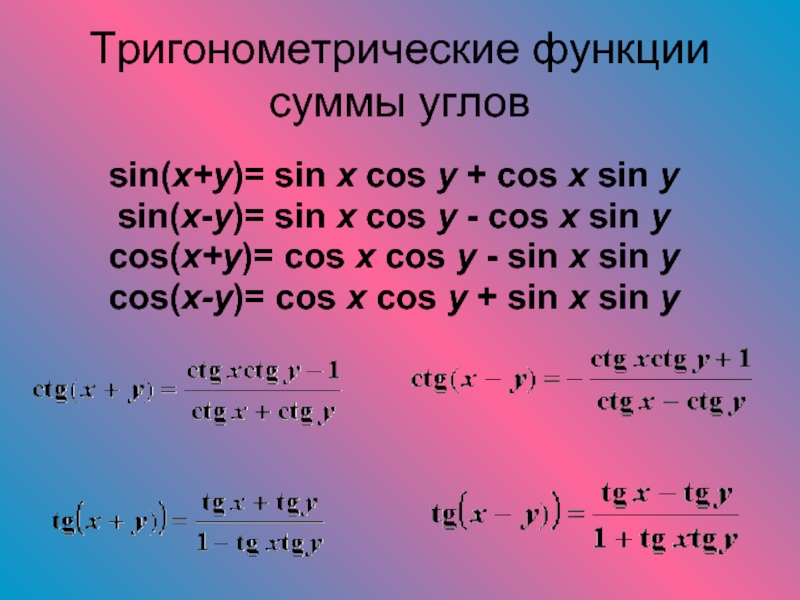Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тригонометрические функции
Содержание
- 1. Тригонометрические функции
- 2. Тригонометрические функции острого угла есть отношения
- 3. П р и м е р
- 4. Для некоторых углов
- 5. Связь тригонометрических функций острого угла
- 6. Тригонометрические функции двойного угла:sin 2x = 2
- 7. Тригонометрические функции половинного углаЧасто бывают полезны формулы,
- 8. Тригонометрические функции суммы угловsin(x+y)= sin x cos
- 9. Для больших значений аргумента можно пользоваться
- 10. Важнейшими тригонометрическими формулами являются формулы сложения,
- 11. Производные всех Тригонометрических функций выражаются через Тригонометрические функции
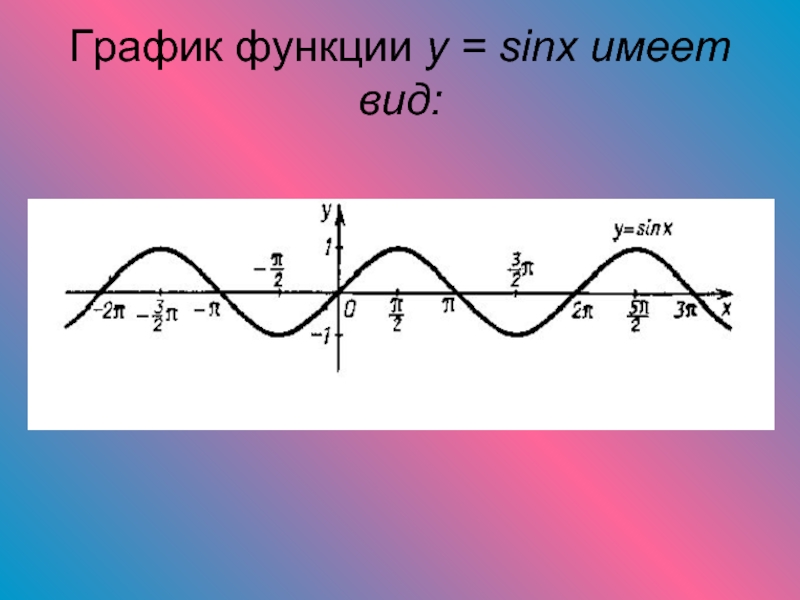
- 12. График функции y = sinx имеет вид:
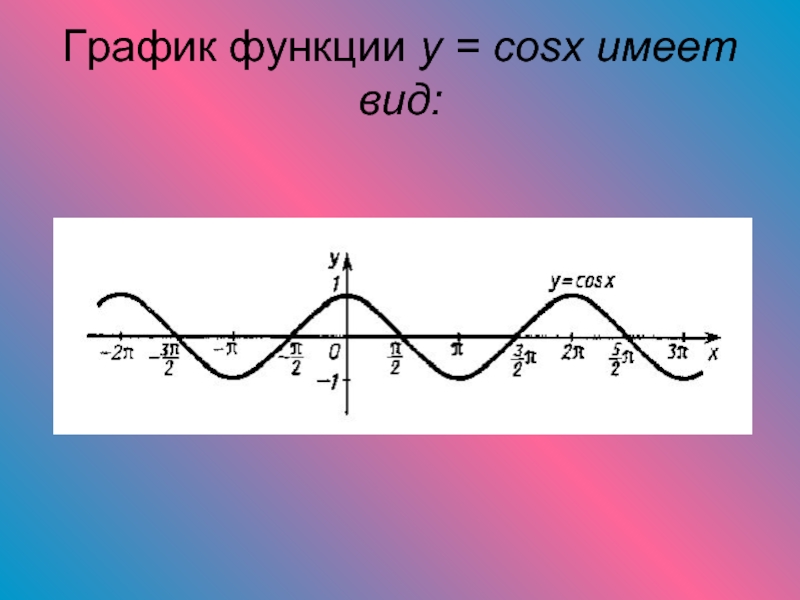
- 13. График функции y = cosx имеет вид:
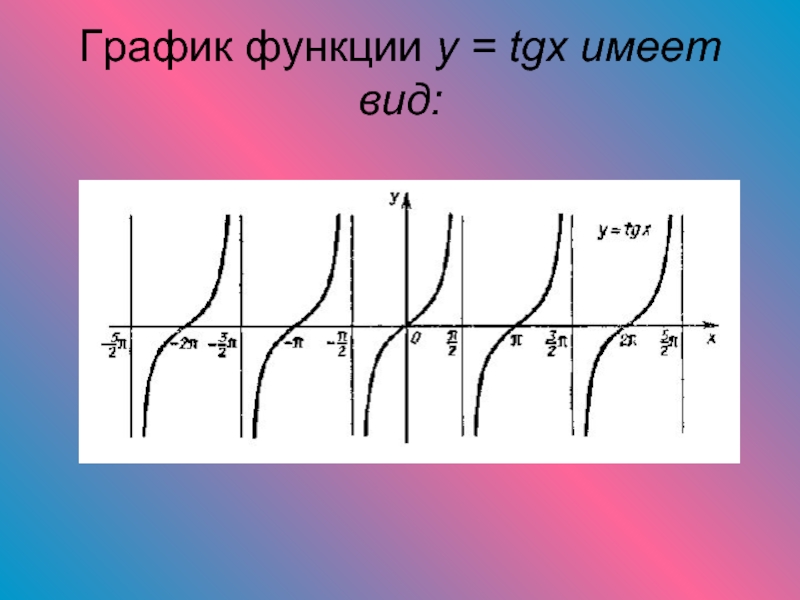
- 14. График функции y = tgx имеет вид:
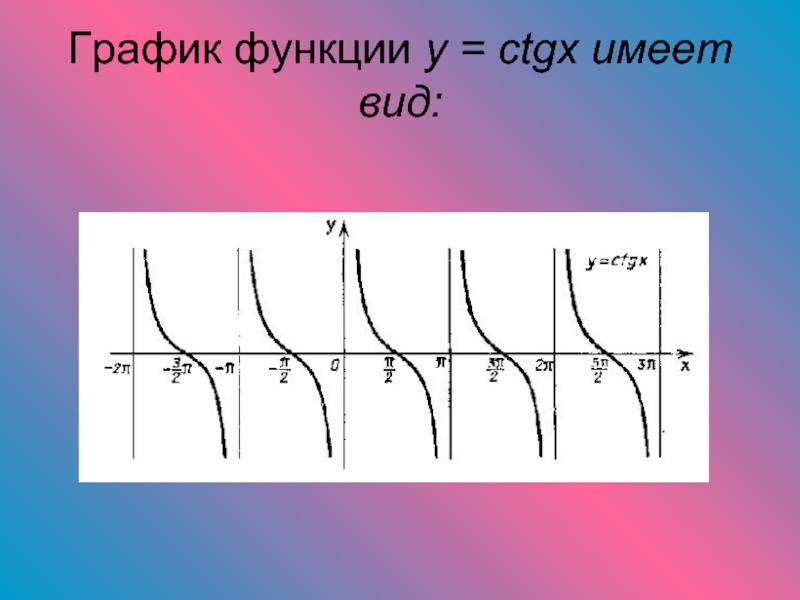
- 15. График функции y = ctgx имеет вид:
- 16. История возникновения тригонометрических функцийТ. ф. возникли
- 17. Гиппархом (2 в. до н. э.),
- 18. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №30»
Тригонометрические функции
Подготовила:
Шунайлова М., ученица 11
«Д»
Слайд 2
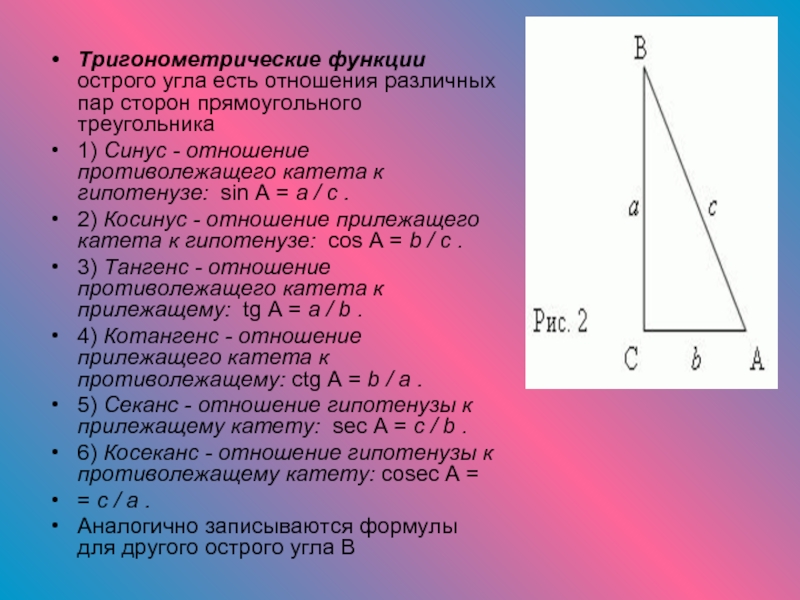
Тригонометрические функции острого угла есть отношения различных пар сторон
прямоугольного треугольника
1) Синус - отношение противолежащего катета к гипотенузе: sin
A = a / c . 2) Косинус - отношение прилежащего катета к гипотенузе: cos A = b / c .
3) Тангенс - отношение противолежащего катета к прилежащему: tg A = a / b .
4) Котангенс - отношение прилежащего катета к противолежащему: ctg A = b / a .
5) Секанс - отношение гипотенузы к прилежащему катету: sec A = c / b .
6) Косеканс - отношение гипотенузы к противолежащему катету: cosec A =
= c / a .
Аналогично записываются формулы для другого острого угла B
Слайд 3
П р и м е р :
Прямоугольный треугольник
ABC ( рис.2 ) имеет катеты:
a = 4, b
= 3. Найти синус, косинус и тангенс угла A.
Р е ш е н и е . Во-первых, найдём гипотенузу, используя теорему Пифагора:
c 2 = a2 + b 2 ,
Согласно вышеприведенным формулам имеем: sin A = a / c = 4 / 5
cos A = b / c = 3 / 5
tg A = a / b = 4 / 3
Слайд 4
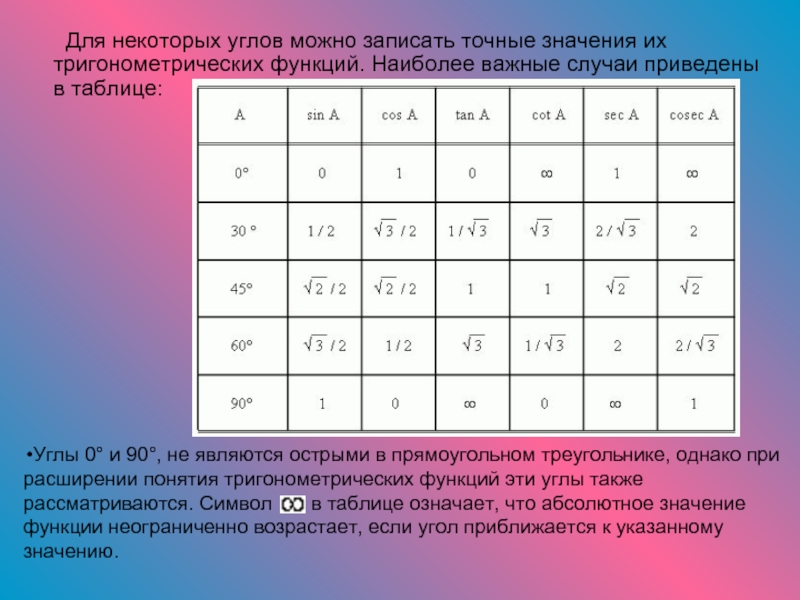
Для некоторых углов можно записать
точные значения их тригонометрических функций. Наиболее важные случаи приведены в
таблице:Углы 0° и 90°, не являются острыми в прямоугольном треугольнике, однако при расширении понятия тригонометрических функций эти углы также рассматриваются. Символ в таблице означает, что абсолютное значение функции неограниченно возрастает, если угол приближается к указанному значению.
Слайд 6Тригонометрические функции двойного угла:
sin 2x = 2 sinx cosx
cos
2x = cos2x - sin2x
tg 2x = 2 tg
x /(1- tg2x)ctg 2x = ctg2x-1/(2 ctg x)
Слайд 7Тригонометрические функции половинного угла
Часто бывают полезны формулы, выражающие степени sin
и cos простого аргумента через sin и cos кратного, например:
Формулы
для cos2x и sin2x можно использовать для нахождения значений Т. ф. половинного аргументаСлайд 8Тригонометрические функции суммы углов
sin(x+y)= sin x cos y + cos
x sin y
sin(x-y)= sin x cos y - cos
x sin y cos(x+y)= cos x cos y - sin x sin y
cos(x-y)= cos x cos y + sin x sin y
Слайд 9
Для больших значений аргумента можно пользоваться так называемыми формулами
приведения, которые позволяют выразить Т. ф. любого аргумента через
Т. ф.
аргумента x, что упрощает составление таблиц Т. ф. и пользование ими, а также построение графиков. Эти формулы имеют вид:в первых трёх формулах n может быть любым целым числом, причём верхний знак соответствует значению n = 2k, а нижний - значению n = 2k + 1; в последних - n может быть только нечётным числом, причём верхний знак берётся при n = 4k + 1, а нижний при n = 4k - 1.
Слайд 10
Важнейшими тригонометрическими формулами являются формулы сложения, выражающие Т. ф.
суммы или разности значений аргумента через Т. ф. этих значений:
знаки
в левой и правой частях всех формул согласованы, то есть верхнему (нижнему) знаку слева соответствует верхний (нижний) знак справа. Из них, в частности, получаются формулы для Т. ф. кратных аргументов, например: