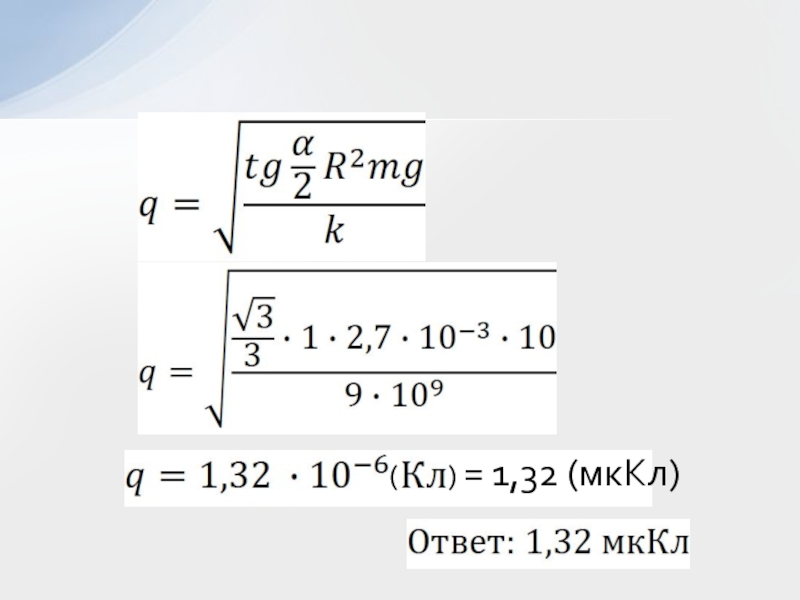Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТРИГОНОМЕТРИЯ И ЕЕ ПРИМЕНЕНИЕ В РАЗЛИЧНЫХ СФЕРАХ НАУКИ И ЖИЗНИ
Содержание
- 1. ТРИГОНОМЕТРИЯ И ЕЕ ПРИМЕНЕНИЕ В РАЗЛИЧНЫХ СФЕРАХ НАУКИ И ЖИЗНИ
- 2. Изучить историю возникновения тригонометрии и понять, как
- 3. ТРИГОНОМЕТРИЯ – (от греч.
- 4. Таблица числовых значений хорд Таблица для
- 5. Архаджива (инд.) - половина тетивы лукаДживаДжибаДжайб (араб.) - выпуклость, пазуха SinusПроисхождение термина «синус»
- 6. Построил таблицы тангенсов, котангенсов и косекансов
- 7. Автор трактата о полном четырехсторонникеПостроил таблицы
- 8. Дополнил и систематизировал различные случаи решения
- 9. Ввел понятие функции и принятую в наши
- 10. С АНРИС. 1С РИС. 2Н cos2 С
- 11. Разработал метод проектирования сложных форм в 1920
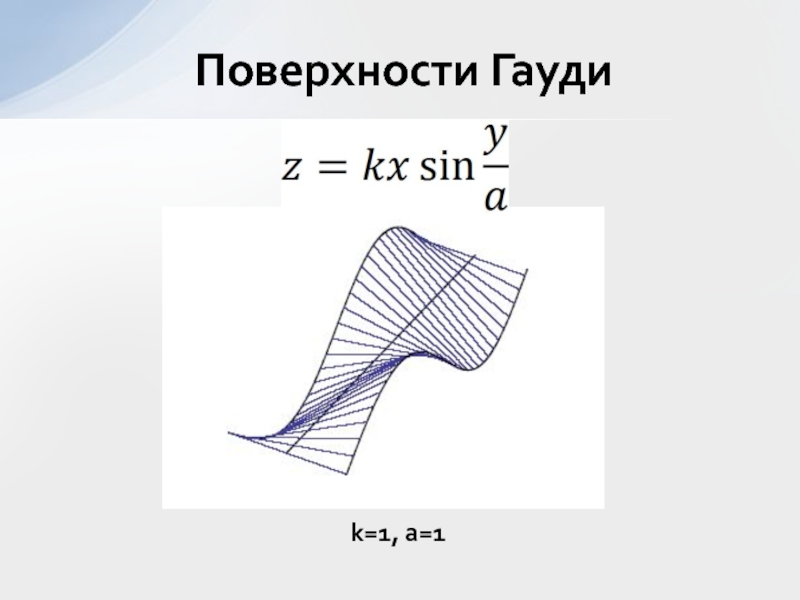
- 12. Поверхности Гаудиk=1, a=1
- 13. Детская школа Гауди в Барселоне
- 14. Страховая корпорация Swiss Re в Лондонеx = λy = f(λ)cos θz = f(λ)sin θ
- 15. Сантьяго Калатрава Винодельня «Бодегас Исиос»
- 16. Феликс Кандела Ресторан в Лос-Манантиалесе[adcos(t) + ddt , bdsin(t), cdt + edt2]
- 17. Готическая архитектура Собор Парижской Богоматери1163г. – середина XIV века.
- 18. Колебания, при которых изменения физических величин
- 19. Скорость – это производная от координаты по
- 20. Слайд 20
- 21. Ускорение – производная от скорости по времени:Вторая
- 22. Слайд 22
- 23. Сравним:иМожно записать:Часто бывает удобно записывать уравнения для
- 24. n1 - показатель преломления первой средыn2 -
- 25. Ка́устика — геометрическое место всех фокусов негомоцентрических пучков
- 26. 1. Сферическая капля 2. Внутреннее отражение
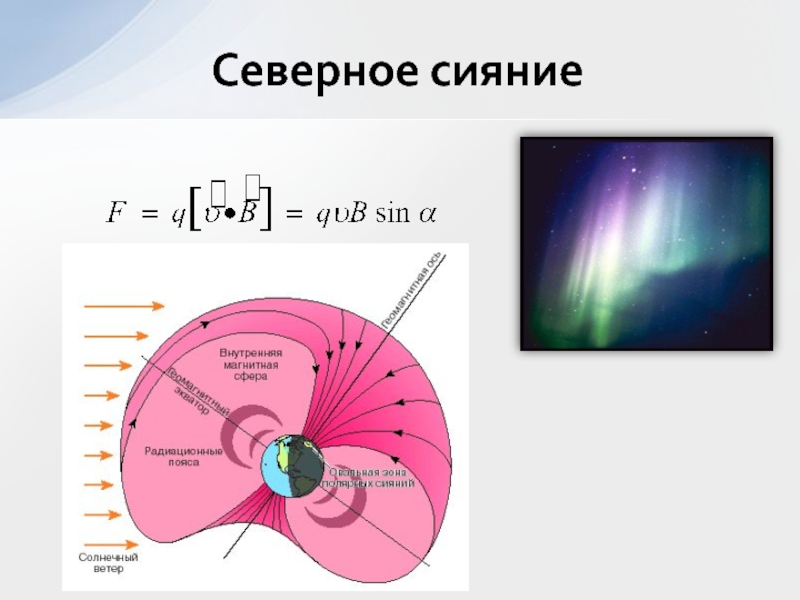
- 27. Северное сияние
- 28. Для двух шкивов, соединенных ременной передачей вычислите
- 29. Случай 11250125012550ACBOO₁αДано:OO₁=1250 ммOB=50 ммO₁C = 125 ммНайти α-? AB = lAC = R- r
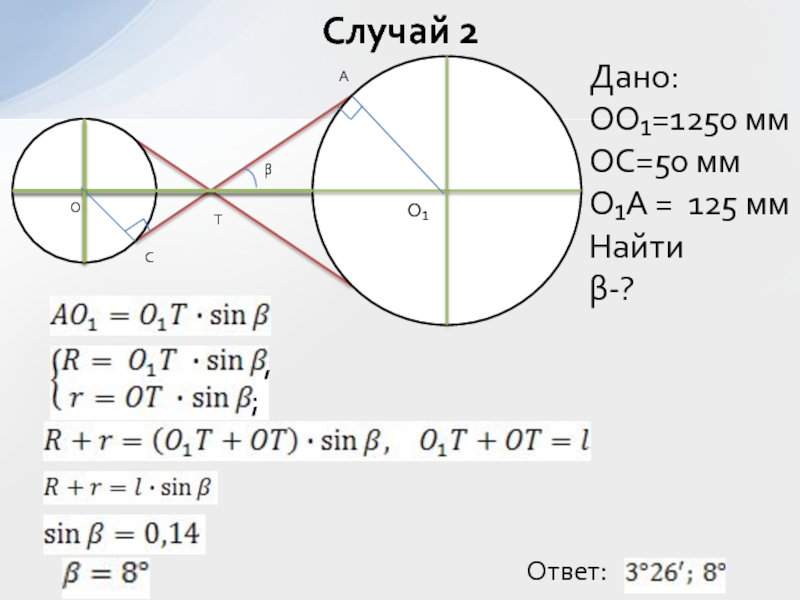
- 30. Ответ:Случай 2O₁OTCAβДано:OO₁=1250 ммOC=50 ммO₁A = 125 ммНайти β-?;,
- 31. С наблюдательного пункта замечают под
- 32. ACHB79,5РешениеHAB = 42°45’BH = 341 мBC =
- 33. На нитях длиной 1 м, закрепленных в
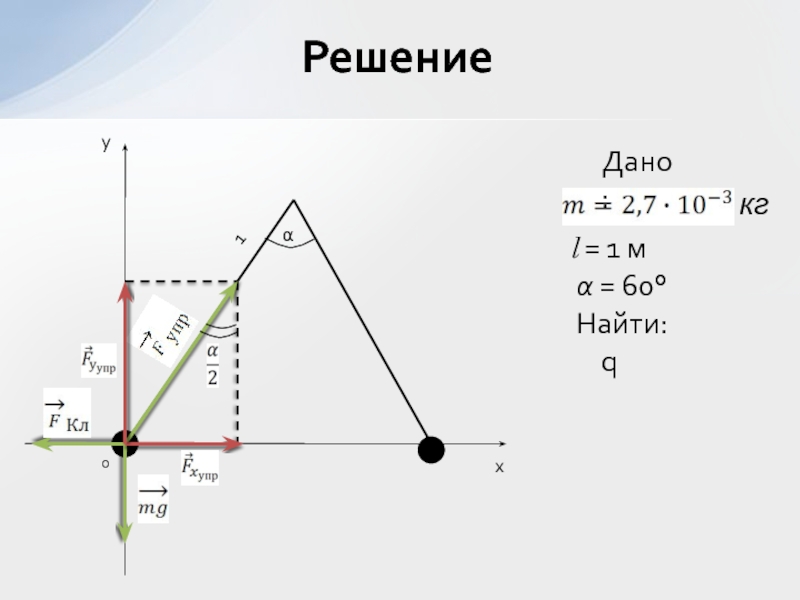
- 34. Решениеxy1l = 1 мкгДано:α = 60°Найти: q0α
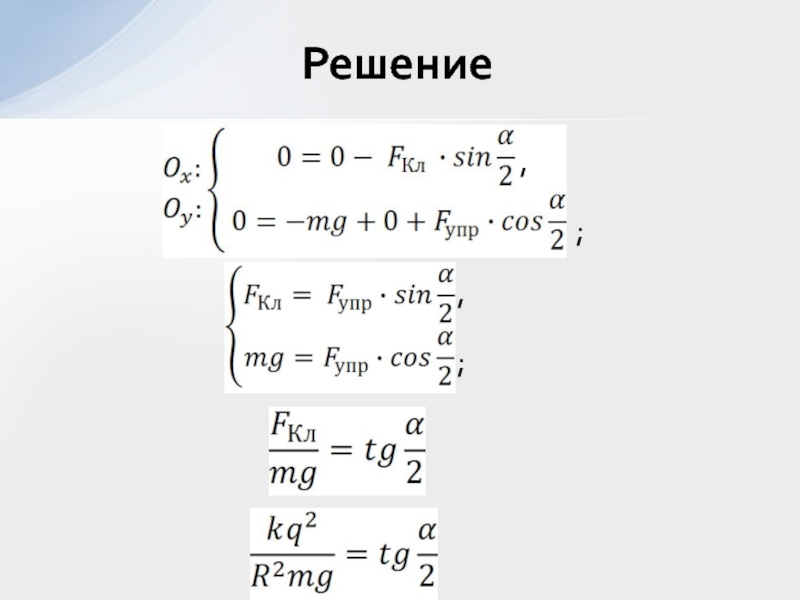
- 35. Решение ;;,,
- 36. ( ) = 1,32 (мкКл)
- 37. Тригонометрия в биологии
- 38. Экологические ритмы : суточные, сезонные (годовые), приливные
- 39. Слайд 39
- 40. Физический цикл -23 дня. Определяет энергию, силу,
- 41. Слайд 41
- 42. Бета-ритм - 14-30 Гц, активная умственная деятельностьАльфа-ритм
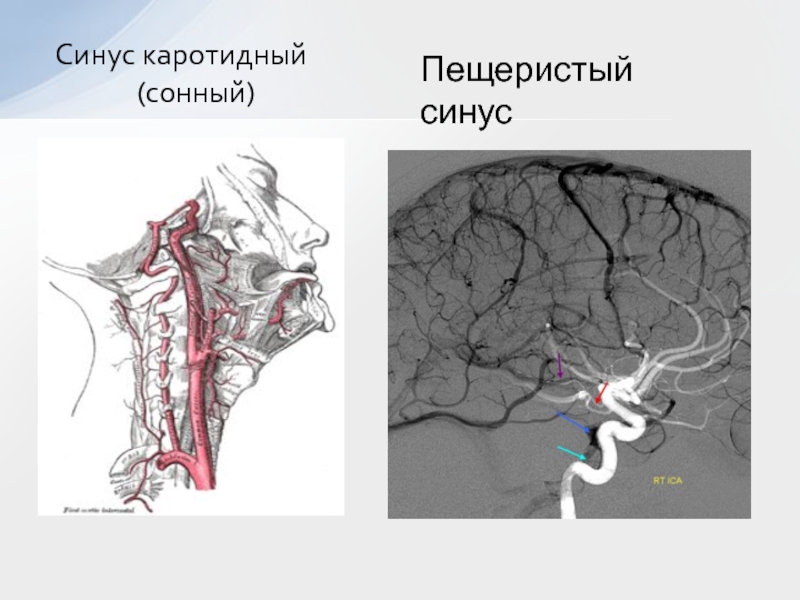
- 43. Синус каротидный (сонный)Пещеристый синус
- 44. В ходе проделанной нами работы
- 45. Скачать презентанцию
Изучить историю возникновения тригонометрии и понять, как зарождались математические понятия, связанные с нейУзнать, в каких сферах науки и искусства применяется тригонометрияИсследовать применение тригонометрии в этих наукахНаучиться использовать знания, полученные на уроках
Слайды и текст этой презентации
Слайд 2Изучить историю возникновения тригонометрии и понять, как зарождались математические понятия,
связанные с ней
Узнать, в каких сферах науки и искусства применяется
тригонометрияИсследовать применение тригонометрии в этих науках
Научиться использовать знания, полученные на уроках алгебры, в задачах с практическим содержанием
Цели работы
Слайд 3 ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник
и metrew – измеряю) – математическая дисциплина, изучающая зависимости между
углами и сторонами треугольников и тригонометрические функции.История тригонометрии
Слайд 4 Таблица числовых значений хорд
Таблица для определения соотношений между
элементами треугольников
Гиппарх Никейский
( 180 – 125 г. до н.э.)
Первая таблица синусов, высчитанная по хордам в окружности«Альмагест – самая значимая тригонометрическая работа всей античности
Клавдий Птолемей (90 – 168 г н.э)
Слайд 5Архаджива (инд.) - половина тетивы лука
Джива
Джиба
Джайб (араб.) - выпуклость, пазуха
Sinus
Происхождение термина «синус»
Слайд 6 Построил таблицы тангенсов, котангенсов и косекансов
Присоединил к линиям
синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов
Установил
основные соотношения между этими линиямиДал определения функциям
Установил формулу двойного угла
Ал-Батани
( ок. 900 г. н.э)
Абу-ль-Вефа
( 940 – 997 г. н.э)
Слайд 7 Автор трактата о полном четырехстороннике
Построил таблицы синусов и котангенсов
Ал-Хорези
(783 – 850 г. н.э)
Насир-эд-Дин из Туса
(1201 –
1274 г. н.э)
Слайд 8 Дополнил и систематизировал различные случаи решения плоских и сферических
треугольников
Открыл «плоскую» теорему косинусов и формулы тригонометрических функций от
кратных угловРазложил функции в ряды и открыл путь для их использования в математическом анализе
Франсуа Виет (1540 – 1603 г.)
Исаак Ньютон
(1643 – 1727г.)
Слайд 9Ввел понятие функции и принятую в наши дни символику
Разъяснил вопрос
о знаках всех тригонометрических функций любого аргумента
Леонард Эйлер
(1707
– 1783 г. н.э)
Слайд 10С
А
Н
РИС. 1
С
РИС. 2
Н
cos2 С + sin2 С
= 1
АС – расстояние от верха статуи до глаз человека,
АН
– высота статуи,sin С - синус угла падения взгляда.
А
Тригонометрия в искусстве
Слайд 11Разработал метод проектирования сложных форм в 1920 году;
Выразил тригонометрические функции
как отношение координат x, y, z к длине элемента.
Ричард Саусвелл
(1888-1970)
![Феликс Кандела Ресторан в Лос-Манантиалесе[adcos(t) + ddt , bdsin(t), cdt + edt2]](/img/thumbs/79a7a83cfb69f029f5c1ccda597c35b0-800x.jpg "ТРИГОНОМЕТРИЯ И ЕЕ ПРИМЕНЕНИЕ В РАЗЛИЧНЫХ СФЕРАХ НАУКИ И ЖИЗНИ Феликс Кандела Ресторан в Лос-Манантиалесе[adcos(t) + ddt , bdsin(t), cdt + edt2]")
Слайд 18 Колебания, при которых изменения физических величин происходят по закону косинуса
или синуса (гармоническому закону), называются гармоническими колебаниями.
Выражение, стоящее под
знаком косинуса или синуса, называется фазой колебания:
Тригонометрия в физике
Слайд 19Скорость – это производная от координаты по времени:
Максимальная скорость колебательного
движения:
Скорость при гармоническом колебании:
Скорость для случая с нулевой начальной фазой:
Слайд 21Ускорение – производная от скорости по времени:
Вторая производная от координаты
по времени:
Максимальное ускорение:
Ускорение при гармоническом колебании:
Ускорение для случая с нулевой
начальной фазой:
Слайд 23Сравним:
и
Можно записать:
Часто бывает удобно записывать уравнения для колебаний
в виде:
Выражение для смещения
Выражение для ускорения
, где
период колебания
Слайд 24
n1 - показатель преломления первой среды
n2 - показатель преломления второй
среды
α-угол падения, β-угол преломления света
Теория радуги
sin β
sin α
n1
n2
=
Слайд 261. Сферическая капля
2. Внутреннее отражение
3. Первичная радуга
4. Преломление
5. Вторичная радуга
6. Входящий луч света
7. Ход лучей при формировании первичной радуги
8. Ход лучей при формировании вторичной радуги
9. Наблюдатель
10-12. Область формирования радуги.
Схема образования радуги
Слайд 28Для двух шкивов, соединенных ременной передачей вычислите углы α при
прямой передаче и β при перекрестной, если диаметры шкивов D=250
мм и d = 100 мм, а расстояние между центрами шкивов l=1250 ммЗадача № 1
Слайд 31 С наблюдательного пункта замечают под углом 63°30’ самолет,
пролетающий над башней, высота которой 79,5 м. Прямая, соединяющая наблюдательный
пункт с верхушкой башни, образует с горизонтальной плоскостью угол 20°45’. На какой высоте находится самолет?Задача № 2
Слайд 32A
C
H
B
79,5
Решение
HAB = 42°45’
BH = 341 м
BC = 341+79,5=420,5 (м)
Дано:
HC =
79,5
HAC = 20°45’
BAC = 63°30’
Найти
BC -?
Ответ: 420,5 м
20°45’
42°45’
Слайд 33На нитях длиной 1 м, закрепленных в одной точке, подвешены
два одинаковых шарика, массой 2,7 г каждый. Когда шарикам сообщили
одноименные заряды, они разошлись и нити образовали угол 60°. Найти заряд каждого шарика.Задача № 3
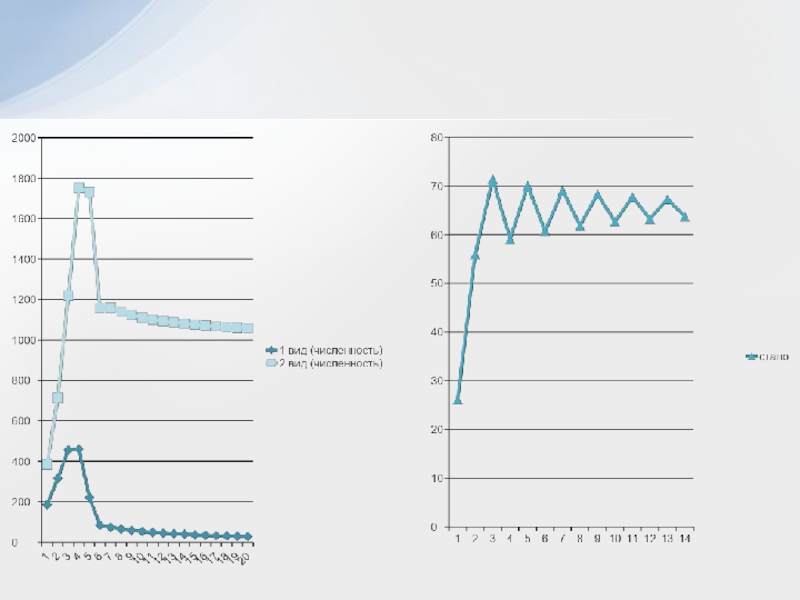
Слайд 38Экологические ритмы : суточные, сезонные (годовые), приливные и лунные циклы
Физиологические
ритмы: ритмы давления, биения сердца, артериальное давление, три биоритма, лежащие
в основе «теории трех биоритмов»Биоритмы
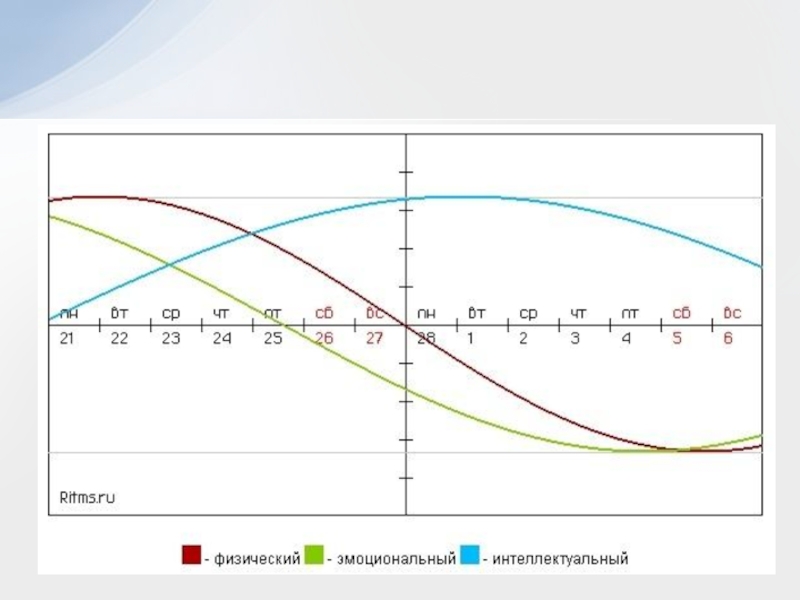
Слайд 40Физический цикл -23 дня. Определяет энергию, силу, выносливость, координацию движения
Эмоциональный
цикл - 28 дней. Состояние нервной системы и настроение
Интеллектуальный цикл
- 33 дня. Определяет творческую способность личностиТеория трех ритмов
Слайд 42Бета-ритм - 14-30 Гц, активная умственная деятельность
Альфа-ритм – 8-13 Гц,
монотонная, рутинная деятельность
Тета-ритм – 4-8 Гц, состояние близкое ко сну,
полудремаДельта-ритм - 1-4 Гц, глубокий сон
Тригонометрия в медицине
Слайд 44 В ходе проделанной нами работы мы:
Выяснили, что тригонометрия
применяется не только в алгебре и началах анализа, но и
во многих других науках, таких как медицина, биология и физикаЯвляется основой для создания многих шедевров искусства и архитектуры
Научились использовать тригонометрию в задачах с практическим содержанием
Вывод
