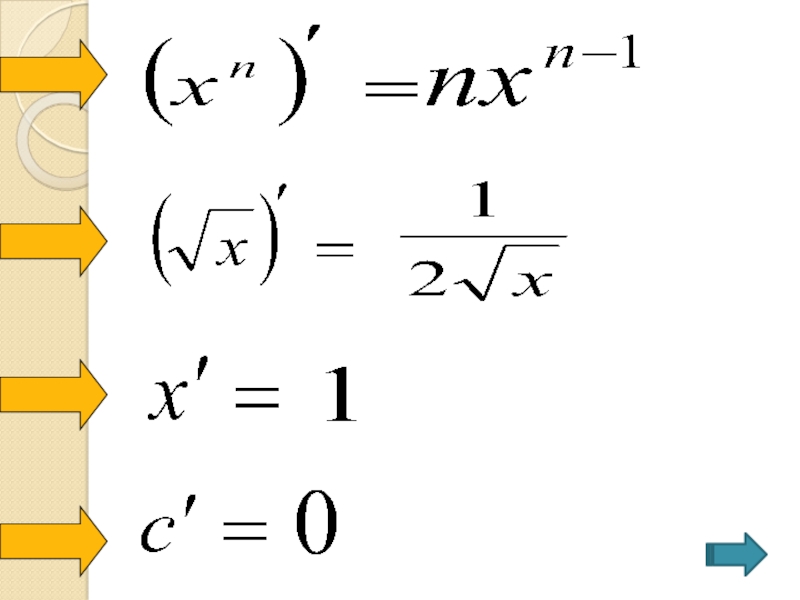Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Туынды тарауын ?айталау ж?не есептер шы?ару
Содержание
- 1. Туынды тарауын ?айталау ж?не есептер шы?ару
- 2. Сабақтың мақсаты:білімділік: Оқушылардың туындысын есептеу ережелері,күрделі,
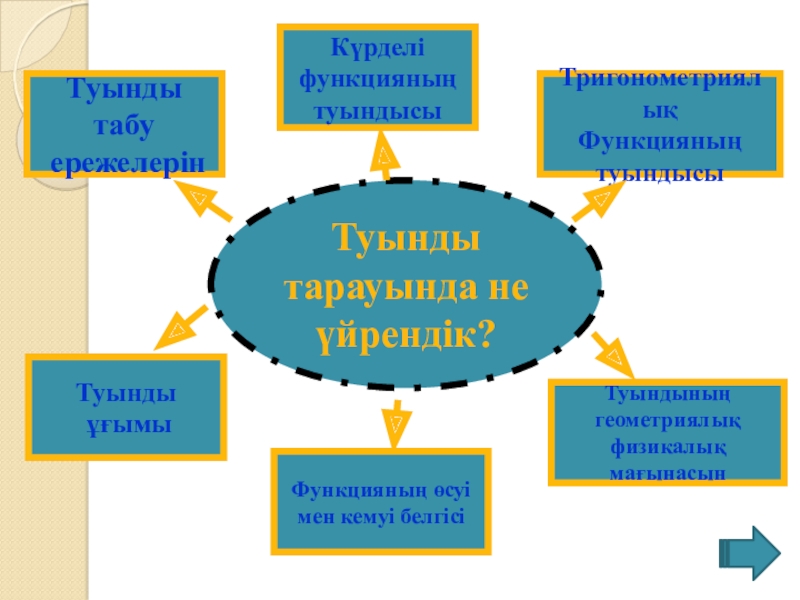
- 3. Туынды тарауында не үйрендік?Туынды табу ережелерінКүрделі функцияныңтуындысыТригонометриялықФункцияныңтуындысыТуынды ұғымыФункцияның өсуі мен кемуі белгісіТуындының геометриялық физикалықмағынасын
- 4. Туынды ұғымы ХVІІ ғасырда пайда болдыбелгіленулерін Лагранж енгізген
- 5. Слайд 5
- 6. Слайд 6
- 7. Күрделі функцияның туындысы Күрделі функция туындысының формуласы. Егер
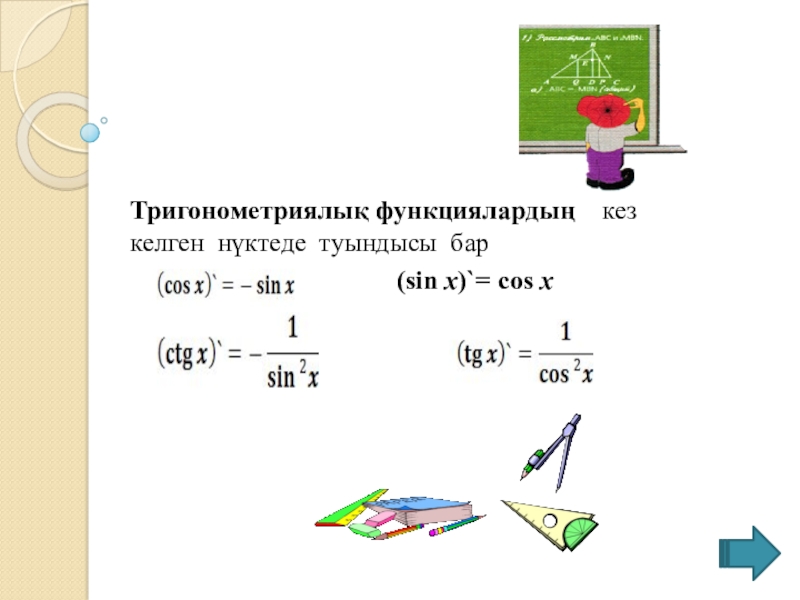
- 8. Тригонометриялық функциялардың кез келген нүктеде туындысы
- 9. Слайд 9
- 10. Слайд 10
- 11. Сәйкестендіру тесті
- 12. (қандай да функцияны формуламен бер)
- 13. Есептер шығаруФункцияның өсетін және кемитін аралықтарын тап
- 14. Слайд 14
- 15. Скачать презентанцию
Сабақтың мақсаты:білімділік: Оқушылардың туындысын есептеу ережелері,күрделі, тригонометриялық функциялардың туындысын,туындының физикалық, геометриялық мағынасы және функцияның өсу, кему аралықтарын табу жөнінде алған білімдерін тереңдету;тәрбиелік: шапшандыққа,ізденімпаздыққа,тиянақтылыққа,
Слайды и текст этой презентации
Слайд 1Туынды тарауын қайталау
және есептер шығару
Дайындаған:
Математика пәнінің мұғалімі
Дадахова Асия Қайыржанқызы
Слайд 2Сабақтың мақсаты:
білімділік:
Оқушылардың туындысын есептеу ережелері,күрделі,
тригонометриялық
функциялардың туындысын,туындының физикалық, геометриялық мағынасы және функцияның өсу, кему аралықтарын
табу жөнінде алған білімдерін тереңдету;тәрбиелік:
шапшандыққа,ізденімпаздыққа,тиянақтылыққа,
ұқыптылыққа баулу,ұжымдық ауыз біршілікке тәрбиелеу;
дамытушылық:
ой-өрісін дамыту,ойлау қабілетін арттыру,теориялық білімін практикада қолдана білу дағдысын қалыптастыру.
Сабақтың әдісі: Қайталау , білімді бекіту сабағы
Слайд 3Туынды
тарауында не
үйрендік?
Туынды табу
ережелерін
Күрделі
функцияның
туындысы
Тригонометриялық
Функцияның
туындысы
Туынды
ұғымы
Функцияның өсуі
мен
кемуі белгісі
Туындының
геометриялық
физикалық
мағынасын
Слайд 7Күрделі функцияның туындысы
Күрделі функция туындысының формуласы.
Егер f функциясының х0
нүктесінде, ал g функциясының у0 = f(х0) нүктесінде туындысы бар
болса, онда күрделі h(х) = g(f(х)) функциясының да х0 нүктесінде туындысы бар болады жәнеh´( х0) = g´ (f(х0)) · f´( х0).
Слайд 9
Физика мен техникадағы туынды
v(t) = х`(t)
Координатаның уақыт бойыншы алынған туындысы
- жылдамдық.Туындының механикалық мағынасы осындай.
Нүктенің қозғалыс жылдамдығы дегеніміз – t уақыттың функциясы. Ал бұл функцияның
туындысы қозғалыс үдеуі деп аталады:
a=v`(t)
Қысқыша былай делінеді: жылдамдықтың уақыт бойынша алынған туындысы – үдеу.
Слайд 10
Функцияның өсу(кему) белгісі
Ф у н к ц и
я н ы ң ө с у і н і ң ж е т к і л і к т і б е л г і с і.Егер I интервалының әрбір нүктесінде f`(x)>0 болса ,
онда f функциясы I интервалында өседі.
Ф у н к ц и я н ы ң к е м у і н і ң ж е т к і л і к т і б е л г і с і.
Егер I интервалының әрбір нүктесінде f`(x)<0 болса ,
онда f функциясы I интервалында кемиді.