Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История развития понятия функции
Содержание
- 1. История развития понятия функции
- 2. История развития понятия функцииФункция - одно из
- 3. Идея функциональной зависимости восходит к древности. Ее
- 4. Понятие переменной величиныГреки рассматривали лишь вопросы, имеющие
- 5. Развитие механики и техникиРазвитие механики и техники
- 6. Само слово “функция” (от латинского functio -
- 7. В 18 веке появляется новый взгляд на
- 8. Развитие понятия функцииСледующий шаг в развитии понятия
- 9. В общем виде понятие обобщенной функции было
- 10. Функцией называется соответствие между двумя множествами, при
- 11. Функции рядом с нами
- 12. Функции рядом с намиЛюбоваться природой можно и
- 13. Знание законов природы дало человеку возможность объяснять
- 14. Функции рядом с намиГрафик делает информацию о
- 15. Функции рядом с нами«…Но кривая линия –
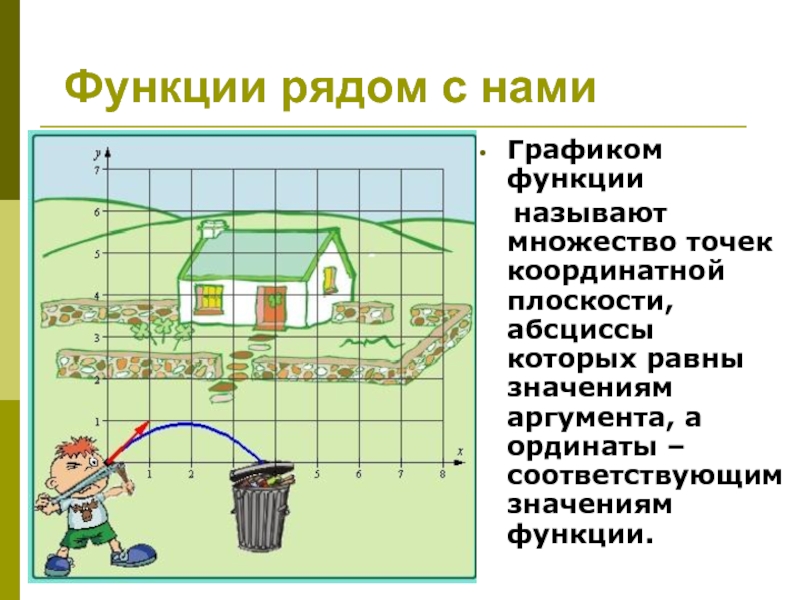
- 16. Функции рядом с намиГрафиком функции
- 17. Функции рядом с намиЧтобы наглядно проиллюстрировать характерные
- 18. С помощью схематичных графиков функции проиллюстрируйте смысл
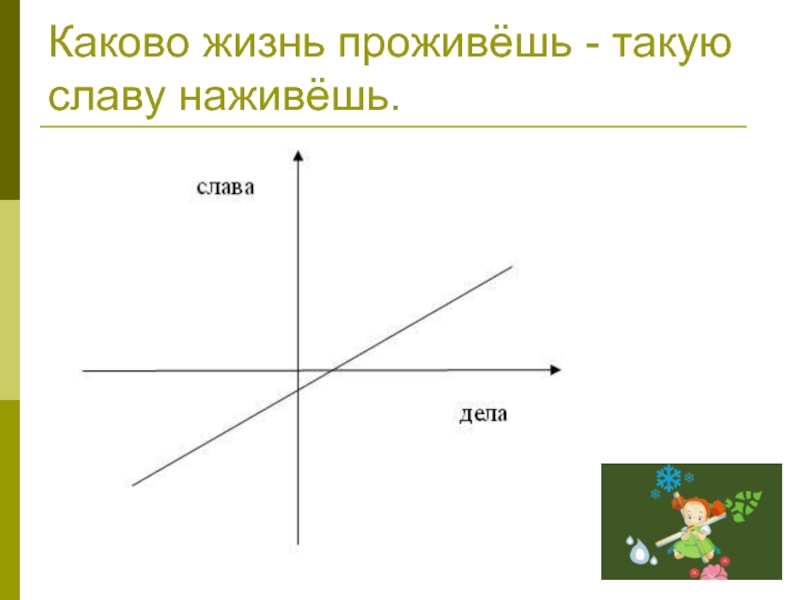
- 19. Каково жизнь проживёшь - такую славу наживёшь.
- 20. функции в нашей жизни
- 21. Диалектика природы«Когда математика стала изучать переменные величины
- 22. Функции в нашей жизниСовременная математика знает множество
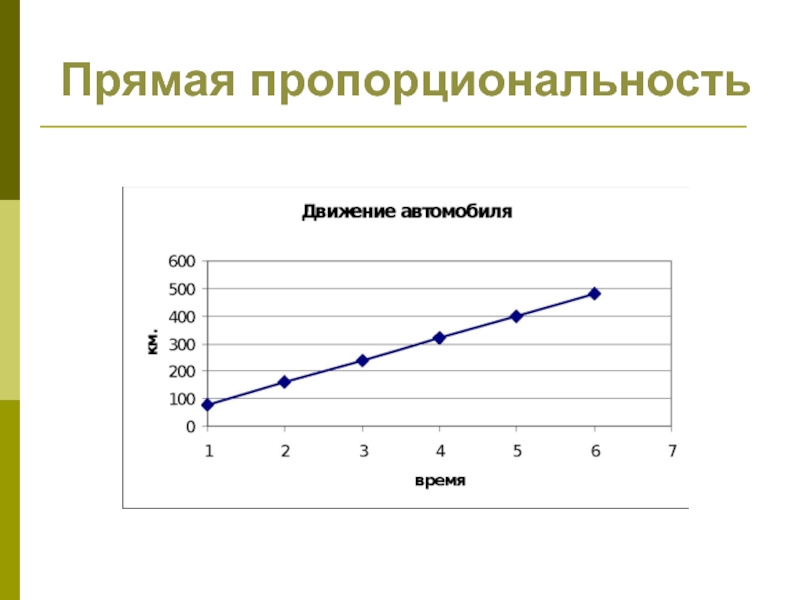
- 23. Прямая пропорциональность
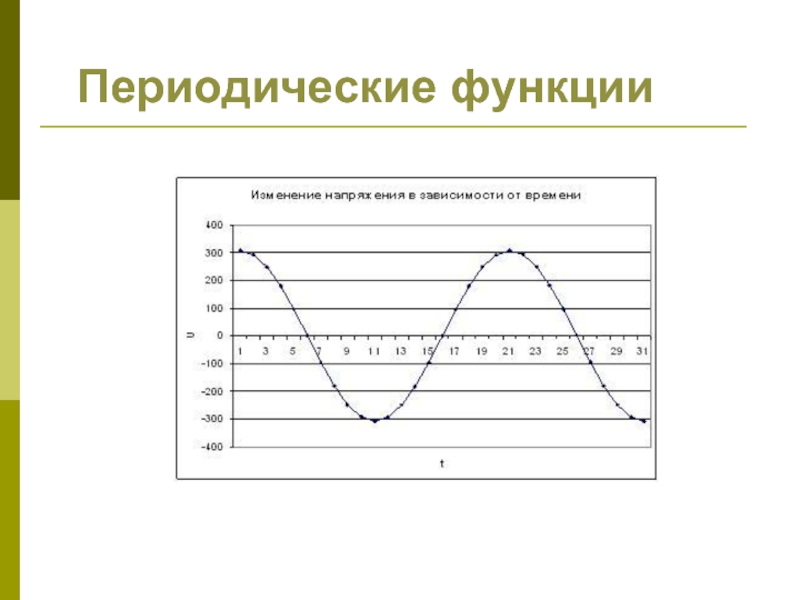
- 24. Периодические функции
- 25. Квадратичная функция Траекторией камня, брошенного под
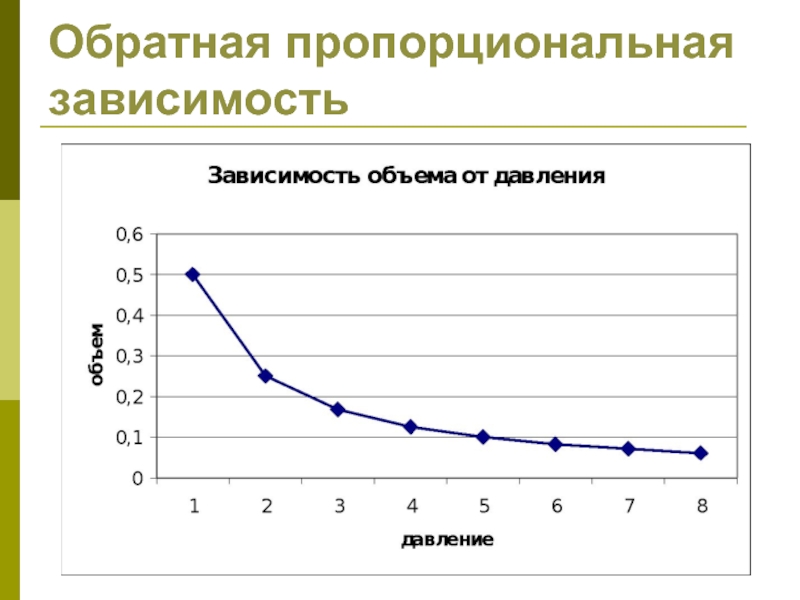
- 26. Обратная пропорциональная зависимость
- 27. Обратная пропорциональная зависимость
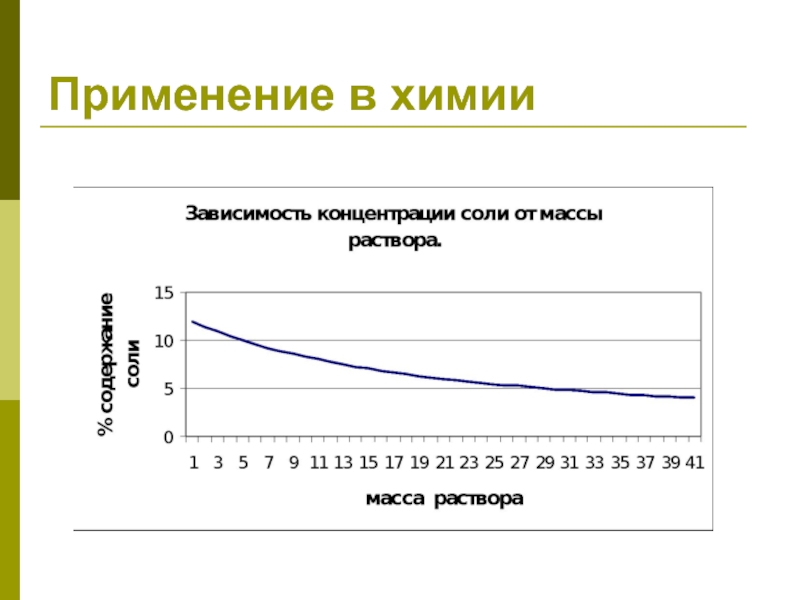
- 28. Применение в химии
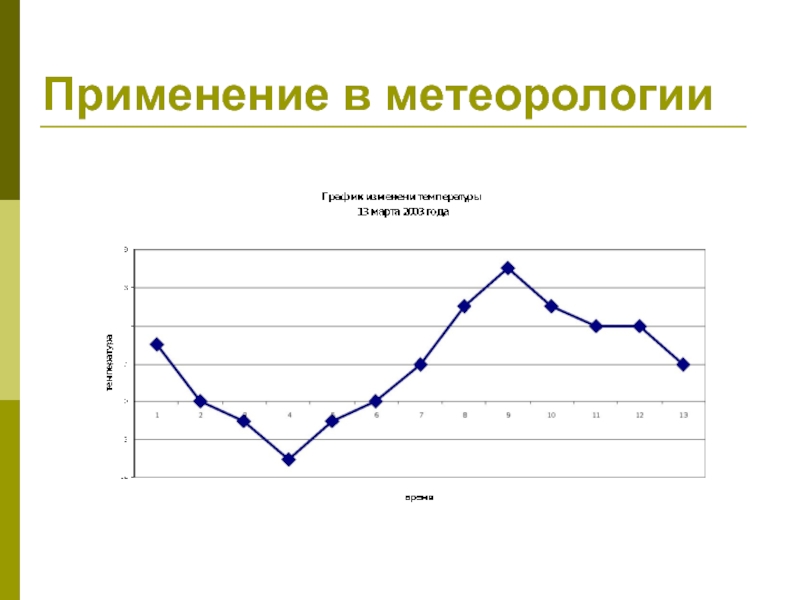
- 29. Применение в метеорологии
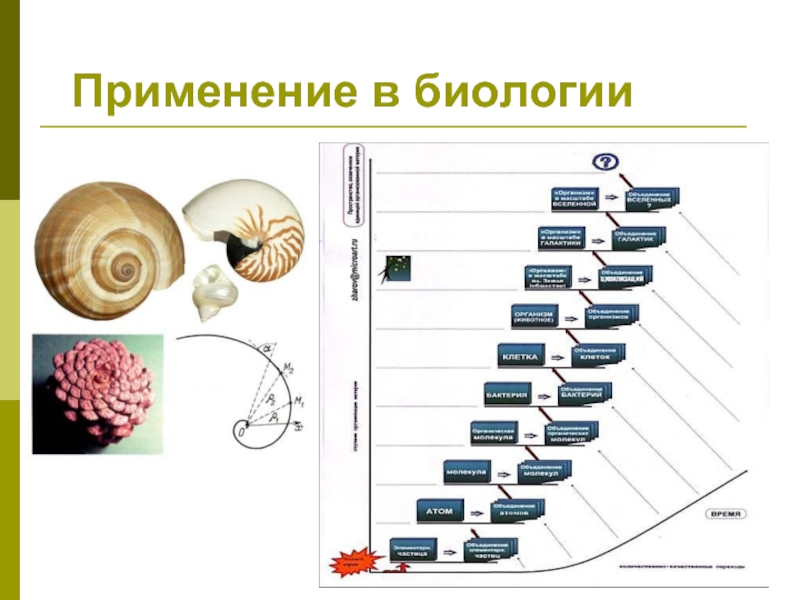
- 30. Применение в биологии
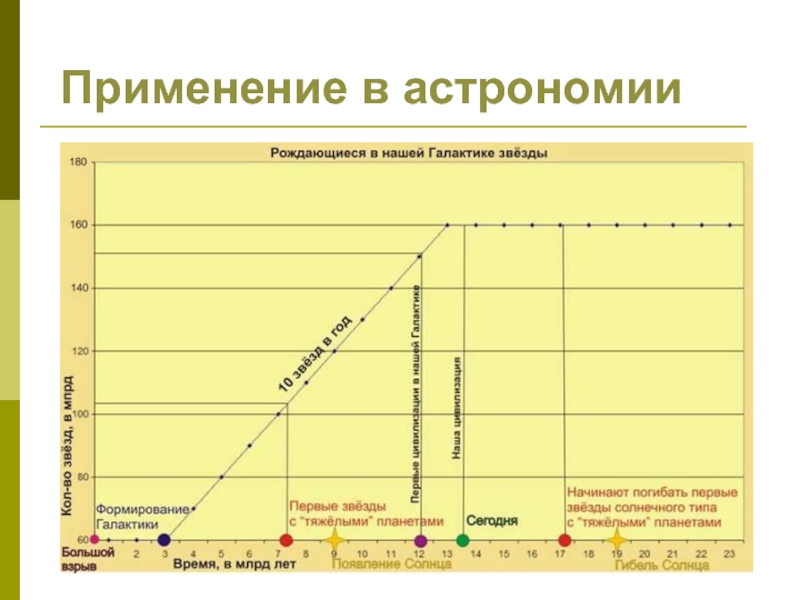
- 31. Применение в астрономии
- 32. Функции в нашей жизниВ наши дни без
- 33. МОУ Гимназия имени академика Н.Г. Басова при
- 34. Скачать презентанцию
История развития понятия функцииФункция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Слайды и текст этой презентации
Слайд 1МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете
Белоусова Алла
Генриховна,
Слайд 2История развития понятия функции
Функция - одно из основных математических и
общенаучных понятий. Оно сыграло и поныне играет большую роль в
познании реального мира.Слайд 3Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже
в первых математически выраженных соотношениях между величинами, в первых правилах
действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур.Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, но установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы:
Слайд 4Понятие переменной величины
Греки рассматривали лишь вопросы, имеющие “геометрическую” природу, и
не ставили вопроса об общем изучении различных зависимостей.
Графическое изображение
зависимостей широко использовали Г. Галилей (1564–1642),
П. Ферма (1601–1665) и
Р. Декарт (1569–1650),
который ввел понятие
«переменной величины».
Рене Декарт
Слайд 5Развитие механики и техники
Развитие механики и техники потребовало введения общего
понятия функции, что было сделано немецким философом и математиком
Г. Лейбницем (1646 – 1716). Слайд 6Само слово “функция”
(от латинского functio - совершение, выполнение) впервые
было употреблено Лейбницем в 1673г. в письме к Гюйгенсу (под
функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону).В печати он ввел этот термин с 1694 года.
Начиная с 1698 года, Лейбниц ввел также термины “переменная” и “константа”.
Слайд 7В 18 веке появляется новый взгляд на функцию как на
формулу, связывающую одну переменную с другой. Это так называемая аналитическая
точка зрения на понятие функции.Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667-1748), который в 1718 году определил функцию следующим образом: “Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных”.
Слайд 8Развитие понятия функции
Следующий шаг в развитии понятия функции сделал гениальный
ученик Бернулли, член Петербургской Академии наук
Леонард Эйлер
(1707 – 1783). Он писал: “Величины, зависящие от других так, что с изменениями вторых изменяются и первые, принято называть их функциями”.
Слайд 9В общем виде понятие обобщенной функции было введено французом Лораном
Шварцем.
В 1936 году, 28-летний советский математик и механик С.
Л. Соболев первым рассмотрел частный случай обобщенной функции.
Слайд 10Функцией называется соответствие между двумя множествами, при котором каждому элементу
одного множества соответствует единственный элемент другого множества.
Слайд 12Функции рядом с нами
Любоваться природой можно и не зная математики.
Но понять ее, увидеть то, что скрыто за внешними образами
явлений можно лишь с помощью точной науки.Только она позволяет заметить, что в явлениях природы есть формы и ритмы, недоступные глазу созерцателя, но открытые глазу аналитика.
Слайд 13Знание законов природы дало человеку возможность объяснять и предсказывать ее
разнообразнейшие явления. «Математическими портретами» закономерностей природы и служит функция.
Функции
рядом с намиСлайд 14Функции рядом с нами
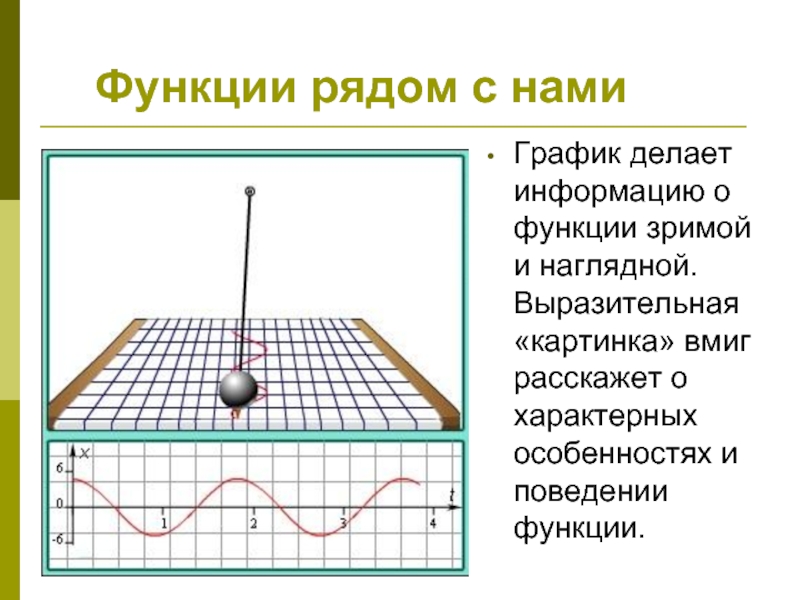
График делает информацию о функции зримой и
наглядной. Выразительная «картинка» вмиг расскажет о характерных особенностях и поведении
функции.Слайд 15Функции рядом с нами
«…Но кривая линия – геометрический эквивалент функции
– гораздо больше говорит воображению, чем формула, и гораздо более
обозрима, чем таблица числовых значений»В.И. Гончаров
Слайд 16Функции рядом с нами
Графиком функции
называют множество
точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты
– соответствующим значениям функции.Слайд 17Функции рядом с нами
Чтобы наглядно проиллюстрировать характерные свойства функции, обратимся
к пословицам. Ведь пословицы – это тоже отражение устойчивых закономерностей,
выверенных многовековым опытом народа.Слайд 18С помощью схематичных графиков функции проиллюстрируйте смысл пословиц:
Каково жизнь проживёшь
- такую
славу наживёшь.
Какой мерой меряешь, такой и
тебе отмерится.
Каши маслом не испортишь.
Чем дальше в лес, тем больше дров.
Дальше от кумы – меньше греха.
Выше меры конь не скачет.
Пересев хуже недосева.
Слайд 21Диалектика природы
«Когда математика стала изучать переменные величины и функции, лишь
только она научилась описывать процессы, движение, так она стала необходима
всем».Фридрих Энгельс.
Слайд 22Функции в нашей жизни
Современная математика знает множество функций, и у
каждой свой «неповторимый облик», как неповторим облик каждого из миллиардов
людей, живущих на Земле.Слайд 25Квадратичная функция
Траекторией камня, брошенного под углом к горизонту,
летящего футбольного мяча или артиллерийского снаряда будет
парабола.
Слайд 32Функции в нашей жизни
В наши дни без функций невозможно не
только рассчитать космические траектории, работу ядерных реакторов, бег океанской волны
и закономерности развития циклона, но и экономично управлять производством, распределением ресурсов, организацией технологичных процессов, прогнозировать течение химических реакций или изменение численности различных взаимосвязанных в природе видов животных и растений, потому что все это – динамические процессы, которые описывает функция.Слайд 33МОУ Гимназия имени академика Н.Г. Басова при Воронежском госуниверситете
Последняя форма
определения функции еще не означает конца ее истории.
Можно не сомневаться,
что в дальнейшем под воздействием новых требований как самой математики, так и других наук – физики, биологии, науки об обществе, определение функции будет изменяться и каждое следующее изменение будет открывать новые горизонты науки и приводить к важным открытиям. С.Л. Соболев
Белоусова А.Г., учитель математики,
кандидат педагогических наук
Теги