Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение касательной
Содержание
- 1. Уравнение касательной
- 2. Ввести понятие касательной к графику функции в
- 3. Умеете ли вы дифференцировать?Правила дифференцированияТаблица производных
- 4. 1. Используя формулы и правила дифференцирования, найдите производные следующих функций:
- 5. Отгадайте фамилию учёного
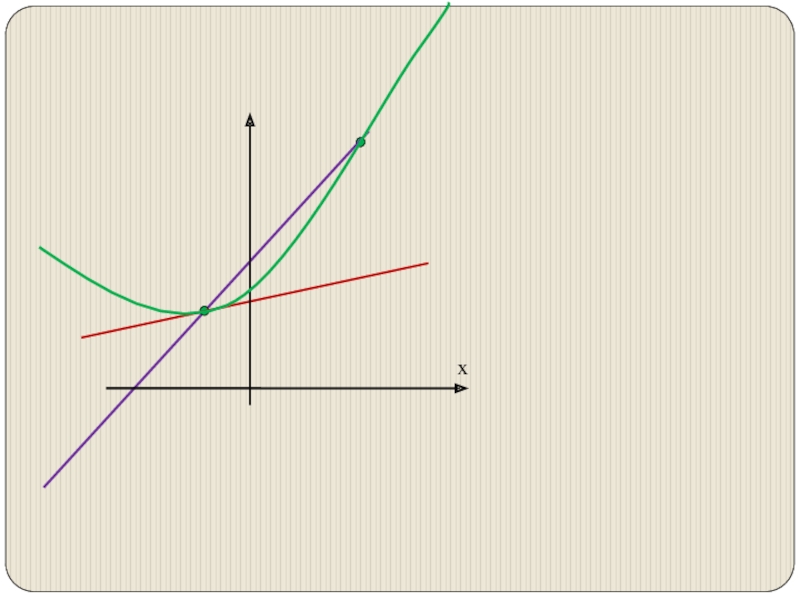
- 6. Сформулируйте определение производной. Какие из указанных прямых
- 7. Касательной к графику функции
- 8. xyy = f(х)ABВT угол TAВ →
- 9. Значение производной функции y= f(x)
- 10. Причем, если : . Геометрический смысл производной
- 11. Пусть в точке А
- 12. 1. Составить уравнение касательной к графику функции
- 13. 2. Составить уравнение касательной к графику функции
- 14. 1.Обозначим абсциссу точки касания буквой x0.2.Вычислим
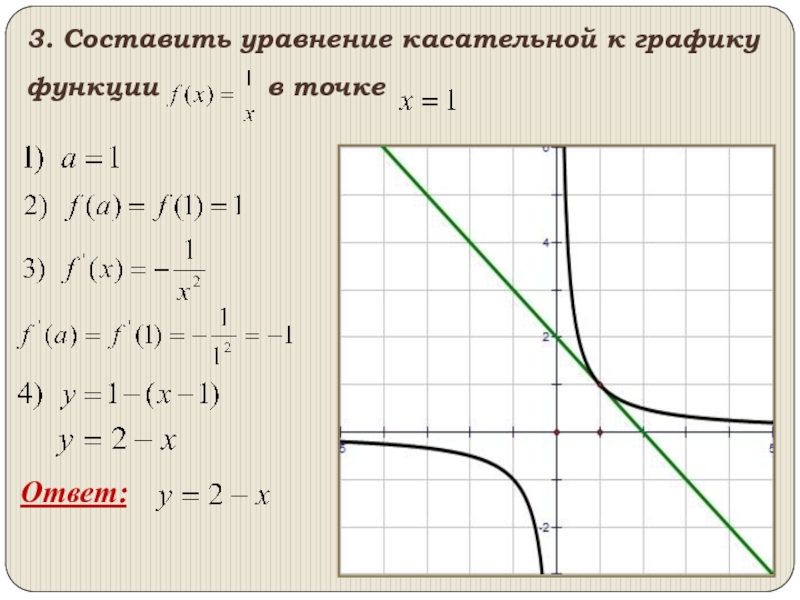
- 15. Ответ: 3. Составить уравнение касательной к графику функции в точке
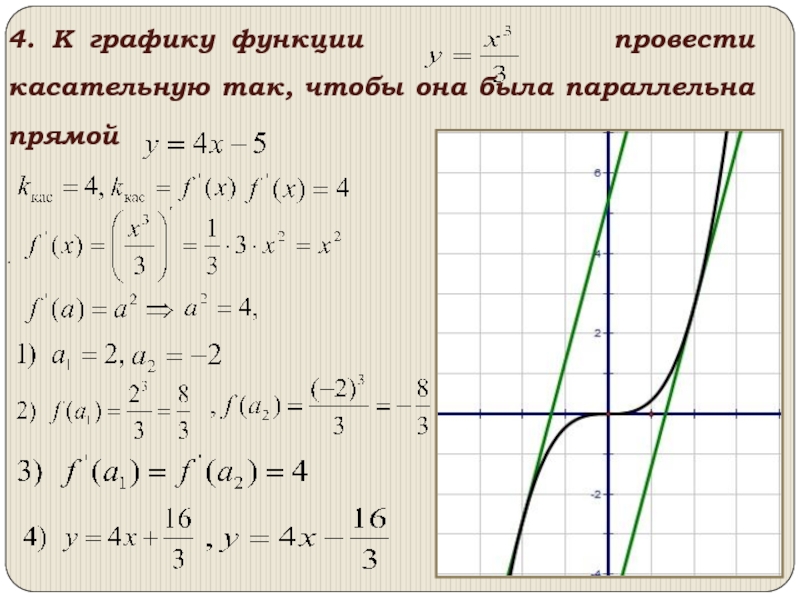
- 16. . , , , , .4. К
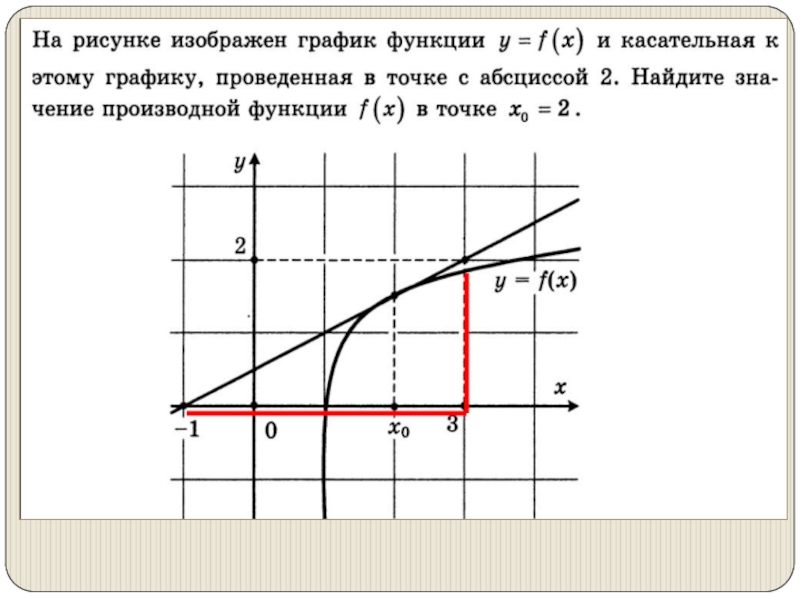
- 17. Слайд 17
- 18. Слайд 18
- 19. Подведение итоговЧто называется касательной к графику функции
- 20. Скачать презентанцию
Ввести понятие касательной к графику функции в точке, выяснить, в чём состоит геометрический смысл производной, вывести уравнение касательной и научить находить его для конкретных функций.Развитие логического мышления, исследовательских навыков, функционального мышления,
Слайды и текст этой презентации
Слайд 1Тема урока:
«Касательная.
Уравнение касательной»
Павловская Нина Михайловна,
учитель математики МБОУ «СОШ
№ 92
Слайд 2Ввести понятие касательной к графику функции в точке, выяснить, в
чём состоит геометрический смысл производной, вывести уравнение касательной и научить
находить его для конкретных функций.Развитие логического мышления, исследовательских навыков, функционального мышления, математической речи.
Выработка коммуникативных навыков в работе
Цель урока
Слайд 6Сформулируйте определение производной.
Какие из указанных прямых параллельны?
у = 0,5х; у = – 0,5х;
у = – 0,5х + 2.Почему?
Ответьте на вопросы:
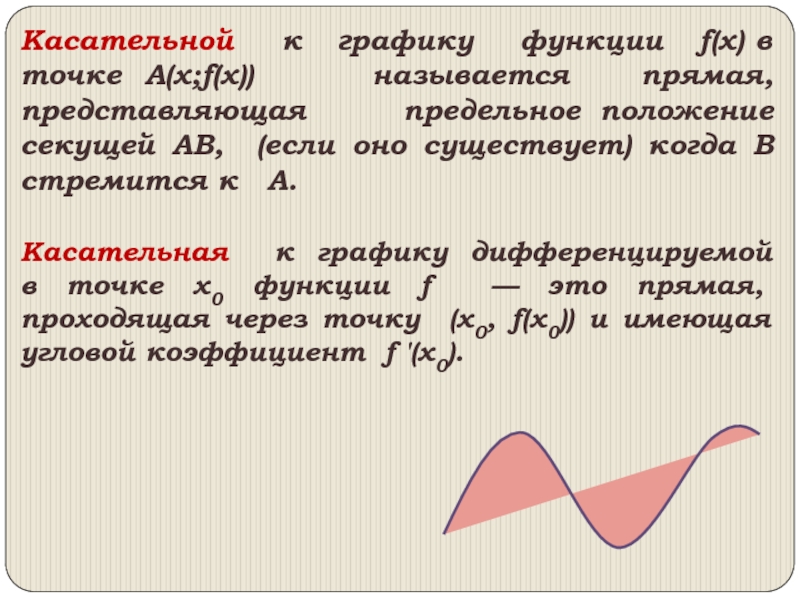
Слайд 7Касательной к графику функции f(x) в
точке А(х;f(х)) называется прямая, представляющая
предельное положение секущей АВ, (если оно существует) когда В стремится к А.Касательная к графику дифференцируемой в точке х0 функции f — это прямая, проходящая через точку (x0, f(x0)) и имеющая угловой коэффициент f '(х0).
Слайд 9Значение производной функции y= f(x) в точке касания
х0 равно угловому коэффициенту касательной к графику функции
y=f(x) в точке х0.Геометрический смысл производной
Слайд 11Пусть в точке А
проведена касательная.
Уравнение любой прямой проходящей через данную точку имеет вид
Слайд 141.Обозначим абсциссу точки касания буквой x0.
2.Вычислим
.
3.Найдем и
.4.Подставим найденные числа x0, и в формулу
Алгоритм нахождения уравнения касательной к графику функции y=f(x).