Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок по теме "Элементы комбинаторики"
Содержание
- 1. Урок по теме "Элементы комбинаторики"
- 2. План занятияПерестановки (определение).Формула числа перестановок из n элементов.Факториал.Решение задач.
- 3. Слайд 3
- 4. Пусть имеются три книги. Обозначим их
- 5. Слайд 5
- 6. Пусть мы имеем n элементов. На
- 7. Слайд 7
- 8. Пример 1. Сколькими способами
- 9. Решение.Число способов равно числу перестановок из 8
- 10. Пример 2. Сколько различных
- 11. Решение. Из цифр
- 12. Пример3. Имеется девять
- 13. Решение. Сначала будем
- 14. Задачи на закрепление пройденного материала.Сколькими способами могут
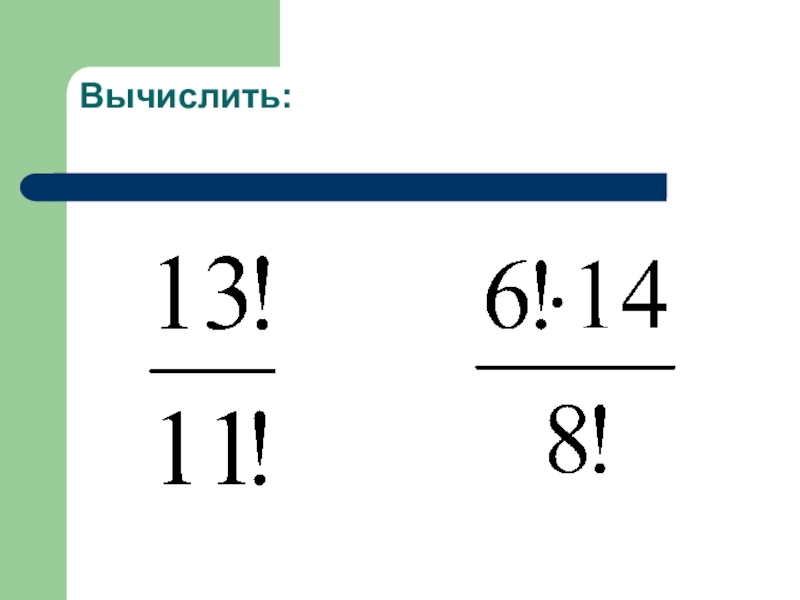
- 15. Вычислить:
- 16. Скачать презентанцию
План занятияПерестановки (определение).Формула числа перестановок из n элементов.Факториал.Решение задач.
Слайды и текст этой презентации
Слайд 2План занятия
Перестановки (определение).
Формула числа перестановок из n элементов.
Факториал.
Решение задач.
Слайд 3 Простейшими комбинациями, которые можно составить из элементов конечного множества, являются
перестановки.
Слайд 4 Пусть имеются три книги. Обозначим их буквами a, b и
с. Эти книги можно расставить на полке по-разному.
Если первой поставить книгу a, то возможны такие расположения книг: abc, acb. Если первой поставить книгу b, то возможными являются такие расположения: bac, bca. И наконец, если первой поставить книгу с, то получим такие расположения: cab, cba. Каждое из этих расположений называют перестановкой из трёх элементов.
Пример.
Слайд 5 Определение Перестановкой из n элементов называется каждое расположение этих
элементов в определённом порядке. Число перестановок
из n элементов обозначают символом (читается «Р из n»).
Слайд 6 Пусть мы имеем n элементов.
На первое место можно
поставить любой из них.
Для каждого выбора первого элемента на второе
место можно поставить один из оставшихся n-1 элементов. Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся
n-2 элементов и т.д.
В результате получим, что
Рn= n (n - 1) ( n – 2) …3·2·1= n!
(читается «n факториал»).
Например, 2!= 2·1=2; 5!=5·4·3·2·1=120.
По определению считают, что 1!=1.
Слайд 7 Таким образом, число всевозможных перестановок из n элементов вычисляется
по формуле:
= n!= 1·2·3·…·(n-2)(n-1)n
Слайд 8Пример 1.
Сколькими способами могут быть расставлены
8 участников финального забега на восьми беговых дорожках?
Слайд 9Решение.
Число способов равно числу перестановок из 8 элементов.
По формуле числа
перестановок находим, что
P8=8!=1·2·3·4·5·6·7·8= 40 320.
Значит, существует 40 320 способов
расстановки участников забега на восьми беговых дорожках.Слайд 10Пример 2.
Сколько различных четырёхзначных чисел,
в
которых цифры не повторяются, можно составить из цифр 0, 2,
4, 6?Слайд 11Решение.
Из цифр 0, 2, 4,
6 можно получить Р4 перестановок. Из этого числа надо исключить
те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с цифры 0. Число таких перестановок равно Р3. Значит, искомое число четырёхзначных чисел (без повторения цифр), которые можно составить из цифр 0, 2, 4, 6, равноР4 - Р3 = 4! – 3! = 24 – 6 = 18.
Слайд 12Пример3.
Имеется девять различных книг, четыре
из которых – учебники.
Сколькими способами
можно расставить эти книги на полке так, чтобы все учебники стояли рядом?Слайд 13Решение.
Сначала будем рассматривать учебники как
одну книгу. Тогда на полке надо расставить не девять, а
шесть книг. Это можно сделать Р6 способами. В каждой из полученных комбинаций можно выполнить Р4 перестановок учебников. Значит, искомое число способов расположения книг на полке равно произведению Р6 · Р4. Получаем:Р6 · Р4 = 6! · 4! = = 17 280.
Слайд 14Задачи на закрепление пройденного материала.
Сколькими способами могут встать в очередь
в билетную кассу:
1) 3 человека; 2) 5 человек?Сколько существует вариантов рассаживания вокруг стола: 1) 6 гостей на 6 стульях; 2) 7 гостей на 7 стульях?
Сколькими способами можно с помощью букв K, L, M и N обозначить вершины четырехугольника?
Сколько различных пятизначных чисел, все цифры которых различны, можно записать с помощью цифр 4, 5, 6, 7 и 8?
Сколькими способами можно расставить на полке 8 книг, среди которых 2 книги одного автора, которые при любых перестановках должны стоять рядом?
В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?