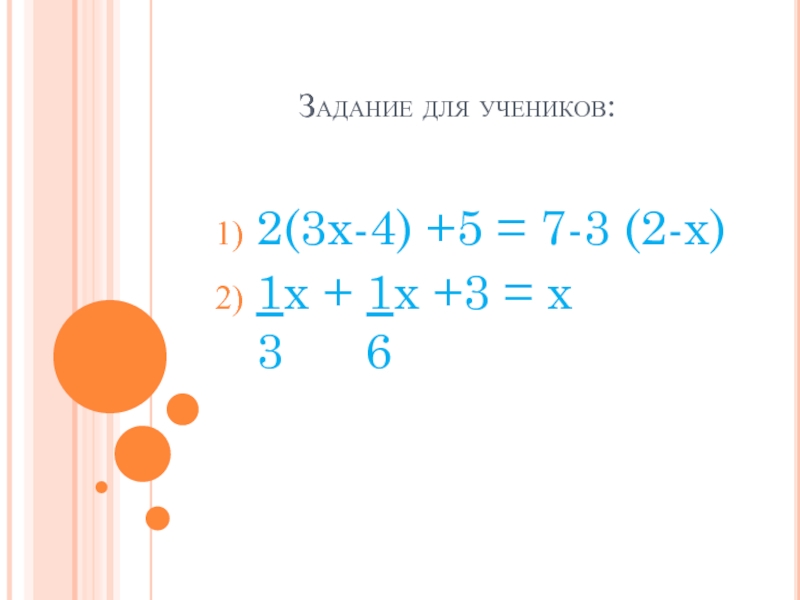Решение линейных уравнений.

Содержание

1. Решение линейных уравнений.
2. Линейное уравнение. Равенство, содержащие неизвестное число,
3. Корень уравнения. Корнем
4. Свойства уравнений. Решить уравнение – это значит
5. Алгоритм решения уравнения:1- упростить левую и правую
6. Если коэффициент при неизвестном в уравнении ax=b
7. Задание для учеников: 2(3x-4) +5 = 7-3
8. Решение №1.А) 2(3x-4) +5=7–3(2-x) 6x-8+5=7-6+3x
9. Решение №2 1x+ 1x + 3 = x;
10. Для домашнего заданияРешите уравнения используя правила. 1) 2y-2 (y-8)=72) 5x – (x-6) = 2(2x+3).
11. Спасибо за внимание.
12. Скачать презентанцию

Линейное уравнение. Равенство, содержащие неизвестное число, обозначенной буквой, называется – уравнением. Выражение, стоящее слева от знака равенства, называется левой частью управления, а выражение стоящее справа от знака равенства, - правой

Главная
Математика
Решение линейных уравнений.

Слайды и текст этой презентации

Слайд 1Решение линейных уравнений.
Подготовила учитель математике. Смирнова А.Н.

Слайд 2Линейное уравнение. Равенство, содержащие неизвестное число, обозначенной буквой, называется –

уравнением.
Выражение, стоящее слева от знака равенства, называется левой частью управления,

а выражение стоящее справа от знака равенства, - правой частью уравнения. Каждое слагаемое левой и правой части уравнения называется членом уравнения.

Линейное уравнение. Равенство, содержащие неизвестное число, обозначенной буквой, называется – уравнением. Выражение, стоящее слева от знака

Слайд 3Корень уравнения.
Корнем уравнения называется то

значение неизвестного, при котором это уравнение обращается в верное числовое

равенство.
Уравнение может иметь один корень: 3x+5=0 Несколько корней: y(y-2)(5+2y) = 0
Бесконечно много корней: 7(x+1) = 7x+7
Уравнение может не иметь корней: x+3=x

Корень уравнения. Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается

Слайд 4Свойства уравнений.
Решить уравнение – это значит найти все его

корни или установить что их нет. При решении уравнений могут

быть использованы свойства уравнения:
1- Корни уравнения не изменяются, если любой член уравнения перенести из одной части уравнения в другую, изменив при этом знак на противоположный.
2 – Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю. Уравнения вида ax=b, где x- неизвестное, a и b – некоторые числа, называются линейным уравнением с одним неизвестным. Решение многих уравнений сводится к решению линейных уравнений .

Свойства уравнений. Решить уравнение – это значит найти все его корни или установить что их нет.

Слайд 5Алгоритм решения уравнения:
1- упростить левую и правую части уравнения (раскрыть

скобки и привести подобные слагаемые, если они есть);
2 – собрать

в левой части уравнения все члены уравнения, содержащие неизвестное, а в правой – не содержащие неизвестное;
3- привести подобные слагаемые в обеих частях уравнения;
4- разделить обе части уравнения на коэффициент при неизвестном (если он не равен нулю).