У=sinX

Содержание

1. У=sinX
2. Функция y=sinx определена на всей числовой прямой,
3. Кривая, являющаяся графиком функции y=sinx, называется синусоидой.
4. Свойства функции y=sinx 1. Область определения -
5. Скачать презентанцию

Функция y=sinx определена на всей числовой прямой, является нечётной и периодической с периодом 2π. График этой функции можно построить таким же способом, как и график функции y=cosx, начиная с построения, например,

Слайды и текст этой презентации

Слайд 1Функция y=sinX

Слайд 2Функция y=sinx определена на всей числовой прямой, является нечётной и

периодической с периодом 2π.
График этой функции можно построить таким

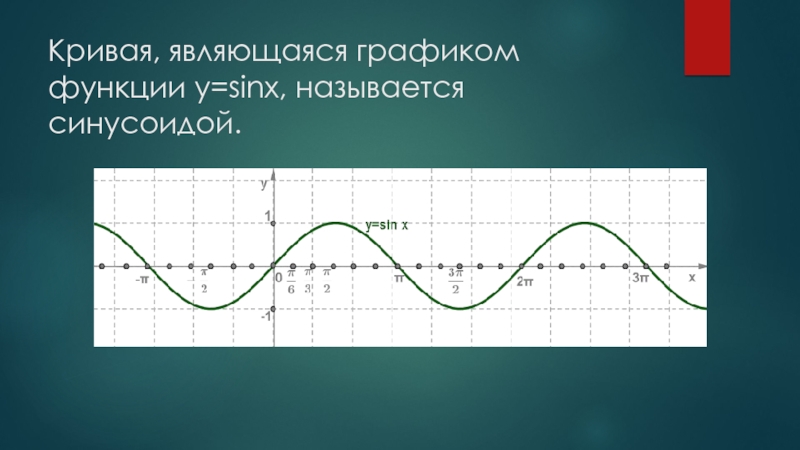
же способом, как и график функции y=cosx, начиная с построения, например, на отрезке [0;π].
Однако проще применить формулу sinx=cos(x−π2), которая показывает, что график функции y=sinx можно получить сдвигом графика функции y=cosx вдоль оси абсцисс вправо на π2

Функция y=sinx определена на всей числовой прямой, является нечётной и периодической с периодом 2π. График этой функции

Слайд 3Кривая, являющаяся графиком функции y=sinx, называется синусоидой.

Слайд 4Свойства функции y=sinx
1. Область определения - множество R всех действительных

чисел.
2. Множество значений - отрезок [−1;1]
3. Функция y=sinx периодическая

с периодом T=2π
4. Функция y=sinx- нечётная.

5. Функция y=sinx принимает:
- значение, равное 0, при x=πn,n∈Z
- наибольшее значение, равное 1, при x=π2+2πn,n∈Z
- наименьшее значение, равное −1, при x=−π2+2πn,n∈Z
- положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
-отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z
- возрастает на отрезке[−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
-убывает на отрезке [π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z