Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устный журнал по математике
Содержание
- 1. Устный журнал по математике
- 2. Автор: Никифорова Татьянаученица 7-а классаРуководитель: Никифорова М.Н., учитель математикиГОУ СОШ №1968Москва
- 3. Пифагор(ок. 570г. – ок. 500г. до н.э.)
- 4. Пифагор - греческий философ, ученый, педагог, политический
- 5. Представить себе эту теорему отдельно от
- 6. Если дан нам треугольникИ притом с прямым
- 7. Доказательство:аbсПусть катеты прямоугольного треугольника равны а и
- 8. Занимательная страница
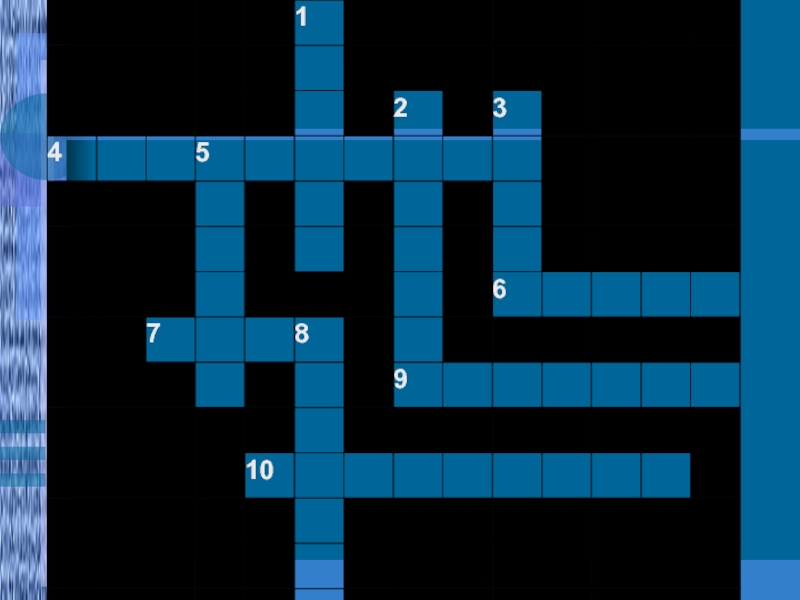
- 9. Кроссворд.
- 10. Слайд 10
- 11. По горизонтали:4.Школьный предмет. 6.Как звали самую известную
- 12. Ребусы.
- 13. РА Н НиЕеЧе БНиК
- 14. Юмористическая страница.
- 15. Как доказать, что ученики ничего не делают?
- 16. Итого остается 137-37=100(дней).4.Но есть еще каникулы: осенние -5дней, зимние-10дней, весенние-7дней, летние-78дней.5.Итак, школьники заняты в году100-100=0(дней).
- 17. Когда же тогда учиться? Где ошибка в рассуждениях?Ответ: (Каникулы и воскресенья подсчитаны дважды.)
- 18. Ответы к кроссвордуПо горизонтали: 4.Математика.
- 19. Ответы к ребусамУравнение.Учебник.Фалес.Пифагор.
- 20. Литература:Энциклопедия «Что такое? Кто такой?»А.Р.Рязановский, Е.А.Зайцев «Дополнительные
- 21. Конец
- 22. Скачать презентанцию
Автор: Никифорова Татьянаученица 7-а классаРуководитель: Никифорова М.Н., учитель математикиГОУ СОШ №1968Москва
Слайды и текст этой презентации
Слайд 2
Автор: Никифорова Татьяна
ученица 7-а класса
Руководитель: Никифорова М.Н., учитель математики
ГОУ СОШ
№1968
Слайд 4Пифагор - греческий философ, ученый, педагог, политический деятель. Согласно Пифагору,
предпосылкой познания мира является чистота души и тела, понимаемые им
как отказ от излишеств, соблюдение определенной диеты и этических правил. Пифагор говорил о бессмертии души, о ее воплощении после смерти и последующего возрождения на земле в животном, соответствующем характеру и поведению человека. Цель научных исследований, по Пифагору, - познание небесной гармонии,законы которой могут быть выявлены при изучении чисел и геометрии. Отсюда обожествление чисел. Совершенной фигурой он считал шар и поэтому впервые высказал теоретическое предположение о шарообразной форме Земли. Ему приписывают формулировку ряда геометрических теорем. Свое учение Пифагор считал доступным немногим избранным и рассматривал своих учеников как товарищество воинствующих борцов со злом, воплощенным в невежестве.
Слайд 5
Представить себе эту теорему отдельно от имени великого грека
уже невозможно, но на самом деле соотношение, которое она утверждает,
было известно древним математикам за много веков до Пифагора.То же соотношение встречается и на вавилонских клинописных табличках, и в древнекитайских, и в древнеиндийских трактатах. Однако в современной истории математики считается, что именно Пифагор дал его первое логически стройное доказательство. Со времен Пифагора появились сотни доказательств знаменитой теоремы, она даже попала в Книгу рекордов Гиннеса.
О наиболее известном частном случае теоремы - «египетском треугольнике» со сторонами 3,4 и 5 – говорится в папирусе, который историки относят к 2000 году до нашей эры.
Теорема Пифагора
Слайд 6Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы
всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И
таким простым путемК результату мы придем.
И.Дырченко
Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 7Доказательство:
а
b
с
Пусть катеты прямоугольного треугольника равны а и b, гипотенуза с.
Достроим
треугольник до квадрата со стороной а+b.
S квадрата (а+b)².
С другой стороны
этот квадрат состоит из 4 равных прямоугольных треугольников и квадрата со стороной с. S каждого треугольника аb и S квадрата с².
S=4· аb+с²=2аb+с²
(а+b)²=2аb+с²; с²=а²+b²
Слайд 11По горизонтали:4.Школьный предмет. 6.Как звали самую известную женщину – математика?7.Французский
математик, чьим именем названа теорема о корнях квадратного уравнения.9.Один из
этапов задачи.10.Равенство с переменной.По вертикали:1.Текстовая запись, в которой содержится вопрос.2.Древнегреческий математик.3.Известный математик, чьим именем названа теорема в геометрии.5.Древнегреческий ученый, создатель геометрии.8.Высказывание, требующее доказательства.
Слайд 15Как доказать, что ученики ничего не делают?
1.По ночам занятий нет,
значит, половина суток свободна. Остается
365-182=183(дня)
2.В школе ученики занимаются половину
дня, значит, вторая половина или четвертая часть суток может быть свободна. Остается 183-183:4=137(дней)
3.В году 52 воскресенья. Из них на каникулы приходится 15 дней, таким образом, выходных в учебном году
52-15=37(дней).
Слайд 16
Итого остается
137-37=100(дней).
4.Но есть еще каникулы: осенние -5дней, зимние-10дней, весенние-7дней,
летние-78дней.
5.Итак, школьники заняты в году
100-100=0(дней).
Слайд 17Когда же тогда учиться?
Где ошибка в рассуждениях?
Ответ:
(Каникулы и воскресенья
подсчитаны дважды.)
Слайд 18Ответы к кроссворду
По горизонтали: 4.Математика.
6.Софья.
7.Виет.
9.Решение.
10.Уравнение.
По вертикали: 1.Задача.
2.Пифагор.
3.Фалес.
5.Евклид.
8.Теорема.
Слайд 20Литература:
Энциклопедия «Что такое? Кто такой?»
А.Р.Рязановский, Е.А.Зайцев «Дополнительные материалы к уроку
математики»
Л.С.Атанасян и др. «Геометрия 7-9»
Г.И.Глейзер «История математики(7-9)»
http://ru.wikipedia.org
http://www.erudition.ru/referat/ref/id.3300_1.html
Теги
